安徽省黄山市休宁县2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-07-03 类型:期中考试
一、单选题
-
1. 下列二次根式为最简二次根式的是( )A、 B、 C、 D、2. 围棋起源于中国,古代称之为“弈”,至今已有 多年的历史. 年 月,世界围棋冠军柯洁与人工智能机器人 进行围棋人机大战.截取首局对战棋谱中的四个部分,由黑白棋子摆成的图案是中心对称的是( )A、
 B、
B、 C、
C、 D、
D、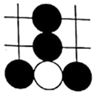 3. 下列各式中计算正确的是( ).A、 B、 C、 D、4. 下列命题的逆命题是真命题的是( )A、对顶角相等 B、全等三角形的对应角相等 C、若 , 则 D、两直线平行,同位角相等5. 已知的三条边分别为a,b,c,下列条件不能判断是直角三角形的是( )A、 B、 , , C、 D、6. 已知a,b,c为的三边长,若满足 , 则是( )A、等边三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形7. 如图,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,经测量AB=2m,则树高为( )米
3. 下列各式中计算正确的是( ).A、 B、 C、 D、4. 下列命题的逆命题是真命题的是( )A、对顶角相等 B、全等三角形的对应角相等 C、若 , 则 D、两直线平行,同位角相等5. 已知的三条边分别为a,b,c,下列条件不能判断是直角三角形的是( )A、 B、 , , C、 D、6. 已知a,b,c为的三边长,若满足 , 则是( )A、等边三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形7. 如图,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,经测量AB=2m,则树高为( )米
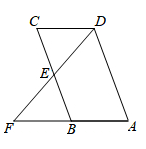
 A、 B、 C、 +1 D、38. 如图,在四边形 中, 是 边的中点,连接 并延长,交 的延长线于点 , .添加一个条件使四边形 是平行四边形,你认为下面四个条件中可选择的是( )
A、 B、 C、 +1 D、38. 如图,在四边形 中, 是 边的中点,连接 并延长,交 的延长线于点 , .添加一个条件使四边形 是平行四边形,你认为下面四个条件中可选择的是( )
 A、 B、 C、 D、9. 平行四边形中,若与小 , 则的度数为( )A、60° B、70° C、80° D、110°10. 如图,已知正方形的边长为4,P是对角线上一点,于点E,于点F,连接 , . 给出下列结论:①;②四边形的周长为8;③一定是等腰三角形;④ . 其中正确结论的序号为( )
A、 B、 C、 D、9. 平行四边形中,若与小 , 则的度数为( )A、60° B、70° C、80° D、110°10. 如图,已知正方形的边长为4,P是对角线上一点,于点E,于点F,连接 , . 给出下列结论:①;②四边形的周长为8;③一定是等腰三角形;④ . 其中正确结论的序号为( ) A、①②③④ B、①②④ C、②④ D、①②③
A、①②③④ B、①②④ C、②④ D、①②③二、填空题
-
11. 要使式子有意义,则的取值范围是 .12. 若最简根式与是同类二次根式,则m= .13. 把 a 中根号外面的因式移到根号内的结果是 .14. 如图,数轴上点A表示的实数为 .
 15. 如图,网格中的每个小正方形的边长都是1,A,B,C三点是小正方形的顶点,则的度数为 .
15. 如图,网格中的每个小正方形的边长都是1,A,B,C三点是小正方形的顶点,则的度数为 . 16. 如图,在平行四边形ABCD中,E为边CD上的一个点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=50°,∠DAE=20°,则∠FED′的大小为 .
16. 如图,在平行四边形ABCD中,E为边CD上的一个点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=50°,∠DAE=20°,则∠FED′的大小为 .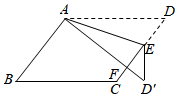 17. 如图,两条宽都为的纸条交叉成60°角重叠在一起,则重叠四边形的面积为 .
17. 如图,两条宽都为的纸条交叉成60°角重叠在一起,则重叠四边形的面积为 . 18. 如图,在的方格纸中小正方形的边长为1,的三个顶点都在小正方形的格点上,下列结论正确的有(填写序号).
18. 如图,在的方格纸中小正方形的边长为1,的三个顶点都在小正方形的格点上,下列结论正确的有(填写序号).①的形状是直角三角形;
②的周长是;
③点B到边的距离是2;
④若点D在格点上(不与A重合),且满足 , 这样的D点有3个不同的位置.

三、解答题
-
19. 计算:(1)、;(2)、 .20. 如图,E,F为平行四边形ABCD的对角线AC所在直线上的两点,AE=CF.求证:∠E=∠F.