北京市燕山区2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-07-03 类型:期中考试
一、单选题
-
1. 在中, , 则的度数为( )A、 B、 C、 D、2. 下列三边的长不能成为直角三角形三边的是( )A、3,4,5 B、4,5,6 C、6,8,10 D、5,12,133. 如图,四边形 是正方形,O , D两点的坐标分别是 , ,点C在第一象限,则点C的坐标是( )
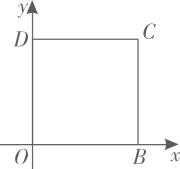 A、 B、 C、 D、4. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、5. 下列二次根式中,能与合并的是( )A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 如图,数轴上点A表示的数为 , 点C表示的数为1, , 且 , 以点A为圆心,长为半径画弧,交数轴正半轴于点 , 则所表示的数为( )
A、 B、 C、 D、4. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、5. 下列二次根式中,能与合并的是( )A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 如图,数轴上点A表示的数为 , 点C表示的数为1, , 且 , 以点A为圆心,长为半径画弧,交数轴正半轴于点 , 则所表示的数为( )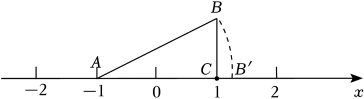 A、 B、 C、 D、8. 如图,直线l上方有三个正方形a,b,c,且正方形a和c的一边在直线l上,正方形b的一个顶点在直线l上,有两个顶点分别与a和c的一个顶点重合.若a,c的面积分别为5和11,则b的面积为( )
A、 B、 C、 D、8. 如图,直线l上方有三个正方形a,b,c,且正方形a和c的一边在直线l上,正方形b的一个顶点在直线l上,有两个顶点分别与a和c的一个顶点重合.若a,c的面积分别为5和11,则b的面积为( )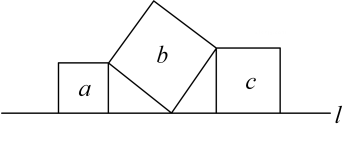 A、6 B、16 C、41 D、55
A、6 B、16 C、41 D、55二、填空题
-
9. 若二次根式 有意义,则x的取值范围是 .10. 比较大小: . (选填“>”、“=”、“<”)11. 菱形的两条对角线的长分别为6和8,则这个菱形的周长为.12. 如图,A,B两点被池塘隔开,为测得A,B两点间的距离,在直线外选一点C,连接和 . 分别取的中点D,E,若测得D,E两点间的距离为 , 则A,B两点间的距离为 .
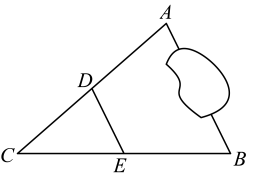 13. 在平行四边形ABCD中,对角线AC,BD交于点O,只需添加一个条件,即可证明平行四边形ABCD是矩形,这个条件可以是(写出一个即可).14. 如图,在直角中, , , 是的中点,则的度数为 .
13. 在平行四边形ABCD中,对角线AC,BD交于点O,只需添加一个条件,即可证明平行四边形ABCD是矩形,这个条件可以是(写出一个即可).14. 如图,在直角中, , , 是的中点,则的度数为 .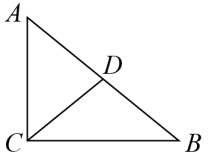 15. 一艘船以20海里/时的速度从A港向东北方向航行,另一艘船以15海里/时的速度从A港向西北方向航行,经过1小时后,它们相距海里.16. 已知:如图,正方形ABCD中,AB=2,AC,BD相交于点O,E,F分别为边BC,CD上的动点(点E,F不与线段BC,CD的端点重合)且BE=CF,连接OE,OF,EF.在点E,F运动的过程中,有下列四个结论:
15. 一艘船以20海里/时的速度从A港向东北方向航行,另一艘船以15海里/时的速度从A港向西北方向航行,经过1小时后,它们相距海里.16. 已知:如图,正方形ABCD中,AB=2,AC,BD相交于点O,E,F分别为边BC,CD上的动点(点E,F不与线段BC,CD的端点重合)且BE=CF,连接OE,OF,EF.在点E,F运动的过程中,有下列四个结论:①△OEF是等腰直角三角形;
②△OEF面积的最小值是;
③至少存在一个△ECF,使得△ECF的周长是;
④四边形OECF的面积是1.
所有正确结论的序号是

三、解答题
-
17. 计算: .18. 计算: .19. 如图,的对角线与交于点O, , , . 求的周长.
 20. 已知 , 求代数式的值.21. 下面是小李设计的“利用直角和线段作矩形”的尺规作图过程.
20. 已知 , 求代数式的值.21. 下面是小李设计的“利用直角和线段作矩形”的尺规作图过程.
已知:如图 , 线段 , , 及 .
求作:矩形 , 使 , .
作法:如图 ,
①在射线 , 上分别截取 , ;
②以为圆心,长为半径作弧,再以为圆心,长为半径作弧,两弧在内部交于点;
③连接 , .
四边形就是所求作的矩形.
根据小李设计的尺规作图过程,解答下列问题:
(1)、使用直尺和圆规,依作法补全图(保留作图痕迹);(2)、完成下面的证明.证明: , ▲ ,
四边形是平行四边形( )(填推理的依据).
,
四边形是矩形( )(填推理的依据).
22. 如图,在菱形ABCD中,E为AB边上一点,过点E作 , 交BD于点M,交CD于点F.求证: .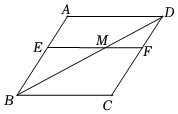 23. 如图,四边形ABCD中,AB=3,BC=4,CD=12,AD=13,且∠B=90°.求四边形ABCD的面积.
23. 如图,四边形ABCD中,AB=3,BC=4,CD=12,AD=13,且∠B=90°.求四边形ABCD的面积.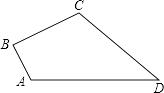 24. 在12世纪印度数学家婆什迦罗的著作中,有一首诗,也称“荷花问题”:
24. 在12世纪印度数学家婆什迦罗的著作中,有一首诗,也称“荷花问题”:平平湖水清可鉴,面上半尺生荷花;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅”
这首诗的大意是:在平静的湖面上,有一朵荷花高出水面半尺,忽然一阵强风吹来把荷花垂直拉到水里且荷花恰好落在水面.此时,捕鱼的人发现,花在水平方向上离开原来的位置2尺远,求湖水的深度.
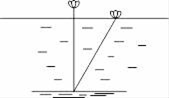 25. 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.已知的顶点都在格点上,且三边长分别为4, , .
25. 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.已知的顶点都在格点上,且三边长分别为4, , . (1)、在图中画出一个满足条件的;(2)、直接写出(1)中所画的面积.26. 如图,在矩形中, , 相交于点O, , .
(1)、在图中画出一个满足条件的;(2)、直接写出(1)中所画的面积.26. 如图,在矩形中, , 相交于点O, , .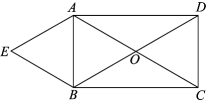 (1)、求证:四边形是菱形;(2)、若 , 求四边形的面积.27. 如图,正方形中,是过点的一条直线,点关于直线的对称点为 , 连接并延长交直线于点 .
(1)、求证:四边形是菱形;(2)、若 , 求四边形的面积.27. 如图,正方形中,是过点的一条直线,点关于直线的对称点为 , 连接并延长交直线于点 .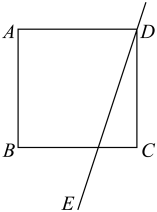 (1)、依题意补全图形;(2)、连接 , 判断的形状并证明;(3)、连接 , 用等式表示线段 , , 之间的数量关系,并证明.28. 对于平面直角坐标系中的两点A和C,给出如下定义:若A,C是某个矩形对角线的顶点,且该矩形的每条边均与x轴或y轴垂直,则称该矩形为点A,C的“对角矩形”.如图1为A,C的“对角矩形”的示意图.已知点 .
(1)、依题意补全图形;(2)、连接 , 判断的形状并证明;(3)、连接 , 用等式表示线段 , , 之间的数量关系,并证明.28. 对于平面直角坐标系中的两点A和C,给出如下定义:若A,C是某个矩形对角线的顶点,且该矩形的每条边均与x轴或y轴垂直,则称该矩形为点A,C的“对角矩形”.如图1为A,C的“对角矩形”的示意图.已知点 .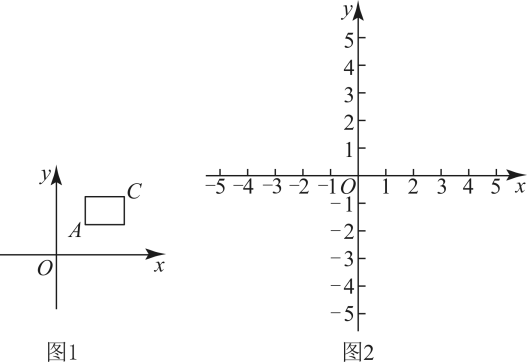 (1)、①当时,在图2中画出点A,C的“对角矩形”,并直接写出它的面积S的值;
(1)、①当时,在图2中画出点A,C的“对角矩形”,并直接写出它的面积S的值;②若点A,C的“对角矩形”的面积是15,求t的值;
(2)、若点 , 在线段上存在一点D,使得点D,C的“对角矩形”是正方形,请直接写出t的取值范围.