河北省石家庄市赵县2022-2023学年八年级下学期数学期中考试试卷

试卷更新日期：2023-07-03 类型：期中考试

进入出卷网下载

一、单选题

1. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{0.2}$ B、 $\sqrt{\frac{1}{2}}$ C、 $\sqrt{6}$ D、 $\sqrt{12}$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{0.4} = 0.2$ B、 $\sqrt{12} = \sqrt{4 \times 3} = 2 \sqrt{3}$ C、 $\sqrt{3} - \sqrt{2} = 1$ D、 $\frac{\sqrt{12}}{3} = 6$

查看试题解析
3. 如图，在四边形ABCD中，下列条件不能判定四边形ABCD是平行四边形的是（）

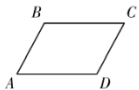A、AB∥DC，AD∥BC B、AB=DC，AD=BC C、AD∥BC，AB=DC D、AB∥DC，AB=DC

查看试题解析
4. 正方形具有而矩形不一定具有的性质是（）

A、四个角都相等 B、对角线互相平分 C、对角线相等 D、对角线互相垂直

查看试题解析
5. 如图，P是面积为S的 $▱ A B C D$ 内任意一点， $△ P A D$ 的面积为 $S_{1}$ ， $△ P B C$ 的面积为 $S_{2}$ ，则（）

A、 $S_{1} + S_{2} > \frac{S}{2}$ B、 $S_{1} + S_{2} < \frac{S}{2}$ C、 $S_{1} + S_{2} = \frac{S}{2}$ D、 $S_{1} + S_{2}$ 的大小与P点位置有关

查看试题解析
6. 已知 $\sqrt{12 - n}$ 是正整数，则实数n的最大值为（）

A、12 B、11 C、8 D、3

查看试题解析
7. 如图，有两块全等的含 $30 °$ 角的直角三角板，将它们拼成形状不同的平行四边形，则最多可以拼成（）

A、1种 B、2种 C、3种 D、4种

查看试题解析
8. 若 $\sqrt{3}$ 的整数部分为x，小数部分为y，则 $\sqrt{3} x - y$ 的值是（）

A、 $3 \sqrt{3}$ B、 $\sqrt{3}$ C、1 D、3

查看试题解析
9. 若a<b(a，b为非零实数)，化简 $\sqrt{- a^{3} b}$ 的结果为 (　　)

A、-a $\sqrt{- a b}$ B、a $\sqrt{- a b}$ C、a $\sqrt{a b}$ D、 $\sqrt{- a b}$

查看试题解析
10. 如图所示，将一根 $24 c m$ 的筷子，置于底面直径为 $15 c m$ ，高 $8 c m$ 的圆柱形水杯中，设筷子露在杯子外面的长度 $h c m$ ，则h的取值范围是（）

A、 $h \leq 17 c m$ B、 $h \geq 8 c m$ C、 $15 c m \leq h \leq 16 c m$ D、 $7 c m \leq h \leq 16 c m$

查看试题解析
11. 如图，在▱ABCD中，AE平分∠BAD，交CD边于E，AD=3，EC=2，则AB的长为（）

A、5 B、3 C、2 D、1

查看试题解析
12. 如图，某同学剪了两条宽均为 $\sqrt{3}$ 的纸条，交叉叠放在一起，且它们的交角为60°，则它们重叠部分的面积为（）．

A、3 B、 $2 \sqrt{3}$ C、 $3 \sqrt{6}$ D、6

查看试题解析
13. 如图，小正方形边长为1，连接小正方形的三个顶点，可得 $△ A B C$ ，则 $A C$ 边上的高长度为（）

A、 $\frac{3 \sqrt{5}}{5}$ B、 $\frac{3 \sqrt{5}}{10}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{\sqrt{5}}{10}$

查看试题解析
14. 某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动．如图，当张角为 $∠ B A F$ 时，顶部边缘B处离桌面的高度 $B C$ 为 $7 c m$ ，此时底部边缘A处与C处间的距离 $A C$ 为 $24 c m$ ，小组成员调整张角的大小继续探究，最后发现当张角为 $∠ D A F$ 时（D是B的对应点），顶部边缘D处到桌面的距离 $D E$ 为 $20 c m$ ，则底部边缘A处与E之间的距离 $A E$ 为（）

A、 $15 c m$ B、 $18 c m$ C、 $21 c m$ D、 $24 c m$

查看试题解析
15. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片，面积分别是2，4，6，8，10，选取其中三块（可重复选取）按图的方式组成图案，使所围成的三角形是面积最大的直角三角形，则选取的三块纸片的面积分别是（）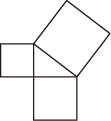

A、2，8，10 B、4，6，10 C、6，8，10 D、4，4，8

查看试题解析
16. 如图，平行四边形 $A B C D$ 的对角线 $A C$ 、 $B D$ 交于点O， $D E$ 平分 $∠ A D C$ 交 $A B$ 于点E， $∠ B C D = 60 °$ ， $A D = \frac{1}{2} A B$ ，连接 $O E$ ．下列结论：① $S_{▱ A B C D} = A D \cdot B C$ ；② $D B$ 平分 $∠ C D E$ ；③ $A O = O E$ ；④ $O E$ 垂直平分 $B D$ ．其中正确的个数有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

17. $\sqrt{(a - 2)^{2}} = 2 - a$ ，则a的取值范围是．

查看试题解析
18. 观察下列各式：
      $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = 1 + \frac{1}{1} - \frac{1}{2} = 1 \frac{1}{2}$ ；
      $\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = 1 + \frac{1}{2} - \frac{1}{3} = 1 \frac{1}{6}$ ；
      $\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = 1 + \frac{1}{3} - \frac{1}{4} = 1 \frac{1}{12}$ ．

(1)、请你根据上面三个等式提供的信息，可以猜想： $\sqrt{1 + \frac{1}{4^{2}} + \frac{1}{5^{2}}}$ ＝；

(2)、利用上述规律计算： $\sqrt{\frac{65}{64} + \frac{1}{81}}$ ＝．（直接写出答案）

查看试题解析
19. 如图，点C在线段AB上，△DAC是等边三角形，四边形CDEF是正方形．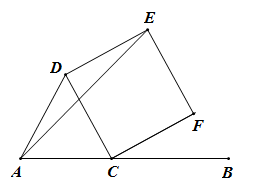

(1)、∠DAE＝°；

(2)、点P是线段AE上的一个动点，连接PB，PC．若AC＝2，BC＝3，则PB＋PC的最小值为．

查看试题解析

三、解答题

20. 计算：

(1)、 $2 \sqrt{20} - \sqrt{5} + 2 \sqrt{\frac{1}{5}}$ ；

(2)、（ $\sqrt{2}$ + $\sqrt{3}$ ）²﹣（ $\sqrt{2}$ + $\sqrt{3}$ ）（ $\sqrt{2}$ ﹣ $\sqrt{3}$ ）．

查看试题解析
21. 如图，某住宅小区在施工过程中留下了一块空地，已知 $A D = 4 m$ ， $C D = 3 m$ ， $∠ A D C = 90 °$ ， $A B = 13 m$ ， $B C = 12 m$ ，小区为美化环境，欲在空地上铺草坪，求这块空地铺满草坪的面积．

查看试题解析
22. 如图， $△ A B C$ 中， $∠ B C A = 90 °$ ， $C D$ 是边 $A B$ 上的中线，分别过点A，C作 $C D ， B A$ 的平行线交于点E，连接 $D E$ 交 $A C$ 于点O，求证：

(1)、四边形 $A D C E$ 是菱形；

(2)、若 $A C = 2 D E = 4$ ，求四边形 $A B C E$ 的面积．

查看试题解析
23. 如图，矩形 $A B C D$ 中， $A B = 4 ， A D = 3$ ，将矩形 $A B C D$ 沿对角线 $A C$ 折叠，点 $B$ 落在点 $E$ 处， $A E$ 交 $C D$ 于点 $F$ ．

(1)、试证明 $△ A C F$ 是等腰三角形；

(2)、求 $C F$ 的长．

查看试题解析
24.

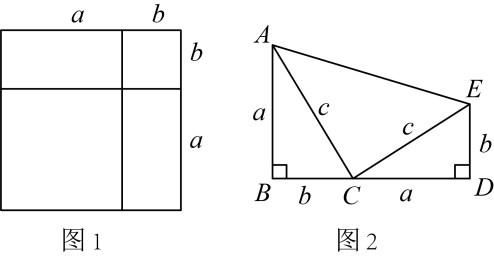(1)、如图1是一个重要公式的几何解释，请你写出这个公式；在推得这个公式的过程中，主要运用了
A．分类讨论思想 B．整体思想 C．数形结合思想 D．转化思想

(2)、如图2， $R t △ A B C ≌ R t △ C D E$ ， $∠ B = ∠ D = 90 °$ ，且 $B ， C ， D$ 在同一直线上．求证： $∠ A C E = 90 °$ ；

(3)、伽菲尔德（1881年任美国第20届总统）利用（1）中的公式和图2证明了勾股定理（发表在1876年4月1日的《新英格兰教育日志》上），请你尝试该证明过程．

查看试题解析
25. 【阅读材料】小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如 $3 + 2 \sqrt{2} = {(1 + \sqrt{2})}^{2}$ ．善于思考的小明进行了以下探索：若设 $a + b \sqrt{2} = {(m + n \sqrt{2})}^{2} = m^{2} + 2 n^{2} + 2 m n \sqrt{2}$ （其中 $a 、 b 、 m 、 n$ 均为整数），则有 $a = m^{2} + 2 n^{2} ， b = 2 m n$ ．这样小明就找到了一种把类似 $a + b \sqrt{2}$ 的式子化为平方式的方法．请你仿照小明的方法探索并解决下列问题：
【问题解决】

(1)、若 $a + b \sqrt{5} = {(m + n \sqrt{5})}^{2}$ ，当 $a 、 b 、 m 、 n$ 均为整数时，则a＝， b＝．（均用含m、n的式子表示）

(2)、若 $x + 4 \sqrt{3} = {(m + n \sqrt{3})}^{2}$ ，且 $x 、 m 、 n$ 均为正整数，分别求出 $x 、 m 、 n$ 的值．

(3)、【拓展延伸】
化简 $\sqrt{5 + 2 \sqrt{6}}$ ＝　　．

查看试题解析
26. 已知正方形 $A B C D$ ，点 $E ， F$ 分别在射线 $A B$ ，射线 $B C$ 上， $A E = B F ， D E$ 与 $A F$ 交于点 $O$ ．

(1)、如图1，当点 $E ， F$ 分别在线段 $A B ， B C$ 上时，则线段 $D E$ 与 $A F$ 的数量关系是，位置关系是．

(2)、如图2，当点 $E$ 在线段 $A B$ 延长线上时，将线段 $A E$ 沿 $A F$ 进行平移至 $F G$ ，连接 $D G$ ．
①依题意将图2补全；

②请你通过实验和观察，试猜想在点 $E$ 运动的过程中线段 $D G ， A D ， A E$ 的数量关系，并证明你的结论．

查看试题解析