山东省菏泽市东明县2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-07-03 类型:期中考试
一、单选题
-
1. 下列垃圾分类标识的图案既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、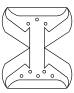 C、
C、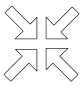 D、
D、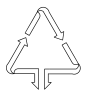 2. 已知 , 下列不等式成立的是( )A、 B、 C、 D、3. 将点沿x轴向左平移4个单位长度得到点 , 点的坐标是( )A、 B、 C、 D、4. 由下列条件不能判定为直角三角形的是( )A、 , , , B、 , , C、 D、5. 如图,在中, , , AD⊥BC于点D . 则的长为( )
2. 已知 , 下列不等式成立的是( )A、 B、 C、 D、3. 将点沿x轴向左平移4个单位长度得到点 , 点的坐标是( )A、 B、 C、 D、4. 由下列条件不能判定为直角三角形的是( )A、 , , , B、 , , C、 D、5. 如图,在中, , , AD⊥BC于点D . 则的长为( )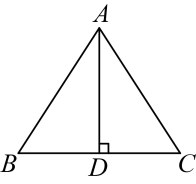 A、8 B、7 C、6 D、56. 一元一次不等式组 的解集在数轴上表示正确的是( )A、
A、8 B、7 C、6 D、56. 一元一次不等式组 的解集在数轴上表示正确的是( )A、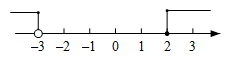
B、
B、 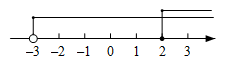
C、
C、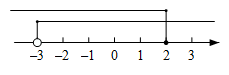
D、
D、
7. 如图,将绕点逆时针旋转得到 , 若且于点 , 则的度数为( )
7. 如图,将绕点逆时针旋转得到 , 若且于点 , 则的度数为( )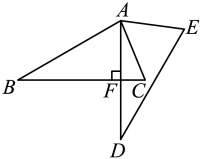 A、 B、 C、 D、8. 如图,在 中,分别以点 和点 为圆心,大于 长为半径画弧,两弧相交于点 , .作直线 ,交 于点 ,交 于点 ,连接 .若 , , ,则 的周长为( )
A、 B、 C、 D、8. 如图,在 中,分别以点 和点 为圆心,大于 长为半径画弧,两弧相交于点 , .作直线 ,交 于点 ,交 于点 ,连接 .若 , , ,则 的周长为( )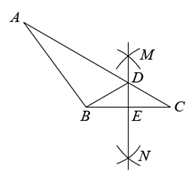 A、25 B、22 C、19 D、189. 若关于的不等式组无解,则的取值范围是( )A、 B、 C、 D、10. 如图所示,在中, , 是的角平分线. , , 垂足分别为E、F,下列选项中错误的是( )
A、25 B、22 C、19 D、189. 若关于的不等式组无解,则的取值范围是( )A、 B、 C、 D、10. 如图所示,在中, , 是的角平分线. , , 垂足分别为E、F,下列选项中错误的是( )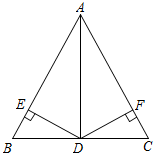 A、且 B、 C、 D、若点P为上任意一点,且 , 则的取值范围是
A、且 B、 C、 D、若点P为上任意一点,且 , 则的取值范围是二、填空题
-
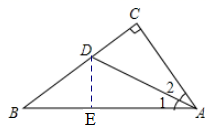
11. 已知△ABC是等腰三角形.若∠A=80°,则△ABC的顶角度数是12. 小张购买笔记本和钢笔共30件,已知每本笔记本2元,每支钢笔5元,费用不超过100元钱,设小张买了x支钢笔,则根据题意可列不等式为.13. 若三角形三边长为3,2x+1,10,则x的取值范围是.14. 如图, , ,若 , ,则D到AB的距离为。
 15. 如图,在中 , , 线段的垂直平分线分别交于点D、E、连接、若 , 则的长为.
15. 如图,在中 , , 线段的垂直平分线分别交于点D、E、连接、若 , 则的长为.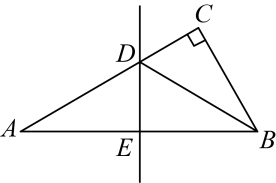 16. 如图,直线与相交于点P,则关于x的不等式的解集为 .
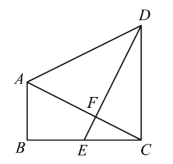
16. 如图,直线与相交于点P,则关于x的不等式的解集为 .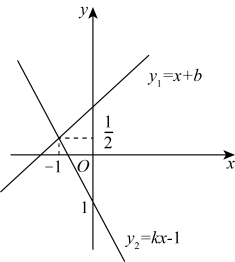 17. 如图.两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到的位置, , 平移距离为6,则阴影部分的面积为 .
17. 如图.两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到的位置, , 平移距离为6,则阴影部分的面积为 .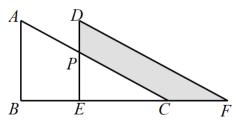 18. 如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点 , , , , …那么点的坐标为.
18. 如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点 , , , , …那么点的坐标为.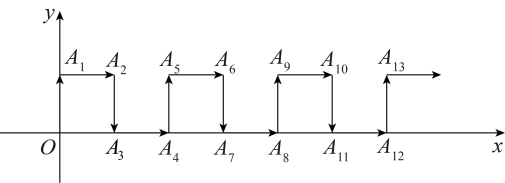
三、解答题
-
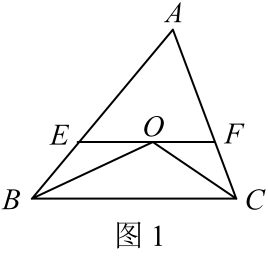
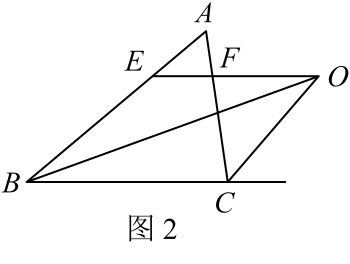
19. 解不等式(组)(1)、(2)、20. 中, , 是中点,于 , 于 , 求证: .
 21. △ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
21. △ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.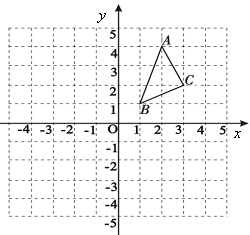 (1)、作出△ABC关于原点O对称的△A1B1C1 , 并写出点C1的坐标;
(1)、作出△ABC关于原点O对称的△A1B1C1 , 并写出点C1的坐标;
(2)、求△ABC的面积.22. 某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球(每个气排球的价格都相同,每个篮球的价格都相同).经洽谈,购买1个气排球和2个篮球共需210元;购买2个气排球和3个篮球共需340元.(1)、每个气排球和每个篮球的价格各是多少元?(2)、该体育馆决定从这家体育用品商店一次性购买气排球和篮球共50个,总费用不超过3200元,且购买气排球的个数少于30个,有哪几种购买方案?