河北省唐山市丰南区2022-2023学年八年级下学期数学期中考试试卷

试卷更新日期：2023-07-03 类型：期中考试

进入出卷网下载

一、单选题

1. 使二次根式 $\sqrt{a - 3}$ 有意义的a的取值范围是（）

A、a>3 B、a<3 C、 $a \geq 3$ D、 $a \leq 3$

查看试题解析
2. 能判定四边形 $A B C D$ 是平行四边形的是（）

A、 $A B ∥ C D$ ， $A D = B C$ B、 $A B = C D$ ， $A D = B C$ C、 $∠ A = ∠ B$ ， $∠ C = ∠ D$ D、 $A B = A D$ ， $C B = C D$

查看试题解析
3. 下列计算正确的是（　　）

A、 $\sqrt{12} - \sqrt{3} = \sqrt{3}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $3 \sqrt{5} \times \sqrt{5} = 4 \sqrt{5}$ D、 $(2 \sqrt{2})^{2} = 4 \sqrt{2}$

查看试题解析
4. 如图，点P是平面坐标系中一点，则点P到原点的距离是（）

A、3 B、 $\sqrt{2}$ C、 $\sqrt{7}$ D、 $\sqrt{53}$

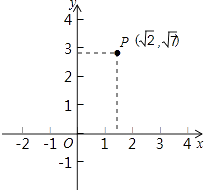查看试题解析
5. 平行四边形的一边长是10cm，那么它的两条对角线的长可以是（）

A、4cm和6cm B、6cm和8cm C、8cm和10cm D、10cm和12cm

查看试题解析
6. 若 $R t △ A B C$ 的两边长a，b满足 ${(a - 4)}^{2} + \sqrt{b - 3} = 0$ ，则第三边的长是（）

A、5 B、 $\sqrt{7}$ C、5或7 D、5或 $\sqrt{7}$

查看试题解析
7. 化简 $\sqrt{\frac{1}{2} + \frac{1}{3}}$ 的结果为（）

A、 $\frac{\sqrt{30}}{6}$ B、 $6 \sqrt{30}$ C、 $\frac{\sqrt{5}}{6}$ D、 $6 \sqrt{5}$

查看试题解析
8.
菱形OACB在平面直角坐标系中的位置如图所示，点C的坐标是（6，0），点A的纵坐标是1，则点B的坐标是（）

A、（3，1） B、（3，-1） C、（1，-3） D、（1，3）

查看试题解析
9. 如图，点O是矩形ABCD的对角线AC的中点，OM//AB交AD于点M，若OM=3，BC=10，则OB的长为（）

A、5 B、4 C、 $\frac{\sqrt{34}}{2}$ D、 $\sqrt{34}$

查看试题解析
10. 如图，△ABC的顶点A，B，C在边长为1的正方形网格的格点上，则BC边上的高为（　　）

A、 $\frac{\sqrt{30}}{2}$ B、 $\frac{8}{5} \sqrt{5}$ C、 $\frac{4}{5} \sqrt{5}$ D、 $\frac{\sqrt{13}}{2}$

查看试题解析
11. 如图，在矩形 $A B C D$ 中，E、F、G、H分别为边 $A B 、 B C 、 C D 、 D A$ 的中点，若 $A B = 4 ， A D = 8$ ，则图中阴影部分的面积为（）

A、6 B、8 C、12 D、16

查看试题解析
12.
如图，正方形ABCD的边长为9，将正方形折叠，使顶点D落在BC边上的点E处，折痕为GH．若BE：EC=2：1，则线段CH的长是（　　）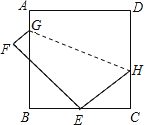

A、3 B、4 C、5 D、6

查看试题解析
13. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 12 c m$ ， $B C = 5 c m$ ，以顶点A为圆心，适当长为半径画弧，分别交 $A C$ 、 $A B$ 于点M、N，再分别以点M、N为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧交于点P，作射线 $A P$ 交边 $B C$ 于点D，则 $C D$ 的值为（）

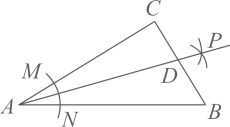A、1 B、2.4 C、3 D、2.5

查看试题解析
14. 如图，将有一边重合的两张直角三角形纸片放在数轴上，纸片上的点A表示的数是-2， $A C = B C = B D = 1$ ，若以点A为圆心， $A D$ 的长为半径画弧，与数轴交于点E（点E位于点A右侧)，则点E表示的数为（）

A、 $\sqrt{3}$ B、 $- 2 + \sqrt{3}$ C、 $- 1 + \sqrt{3}$ D、 $- \sqrt{3}$

查看试题解析

二、填空题

15. 计算： $\sqrt{27}$ ﹣ $\sqrt{12}$ = ．

查看试题解析
16. 如图，由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形．直角三角形的两直角边分别为a、b，若ab=6，小正方形的面积是1，则大正方形的边长是．

查看试题解析
17. 如图，正方形 $B E F G$ 的面积为5，正方形 $A B C D$ 的面积为7．

(1)、线段 $C E$ 的长度是；

(2)、 $△ G C E$ 的面积是．

查看试题解析
18. 如图， $△ A B C$ 中， $A B = 3 ， A C = 4 ， B C = 5$ ，P为边 $B C$ 上一动点， $P E ⊥ A B$ 于点E， $P F ⊥ A C$ 于F．

(1)、四边形 $A E P F$ 是哪种特殊的四边形？答：；

(2)、 $E F$ 的最小值为．

查看试题解析

三、解答题

19.

(1)、计算： $(3 + 2 \sqrt{2}) (3 - 2 \sqrt{2}) - \sqrt{54} \div \sqrt{6}$

(2)、先化简，再求值： $(1 - \frac{1}{x + 1}) \div \frac{x^{2}}{x + 1}$ 其中x的值为 $\sqrt{2}$

查看试题解析
20. 如图，菱形 $A B C D$ 中，对角线 $A C 、 B D$ 交于点O．

(1)、若 $∠ B A D = 60 °$ ，则 $∠ A D C =$ ， $△ B A D$ 是三角形（按边分类）；

(2)、如图，点E是 $B D$ 上一点，则 $A E$ 与 $C E$ 有怎样的数量关系？并证明．

查看试题解析
21. 如图，嘉嘉在荡秋千时发现，秋千 $A C$ 在静止位置时，下端 $C$ 离地面 $0.6$ 米，荡秋千到 $A B$ 位置时，下端 $B$ 距静止位置的水平距离 $E B$ 等于 $2.4$ 米，距地面 $1.4$ 米，求秋千 $A B$ 的长．

查看试题解析
22. 如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E．

(1)、 $∠ A C B$ 的大小＝°；

(2)、求证： $△ A B E$ ≌ $△ A D E$ ；

(3)、若 $∠ C B F = 20 °$ ，则 $∠ A E D$ 的大小＝°．

查看试题解析
23. 观察下列各式：① $\sqrt{1 + \frac{1}{3}} = 2 \sqrt{\frac{1}{3}}$ ， ② $\sqrt{2 + \frac{1}{4}} = 3 \sqrt{\frac{1}{4}}$ ；③ $\sqrt{3 + \frac{1}{5}} = 4 \sqrt{\frac{1}{5}}$ ， …

(1)、请观察规律，并写出第④个等式：　　；

(2)、请用含n（n≥1）的式子写出你猜想的规律：　　；

(3)、请证明（2）中的结论．

查看试题解析
24. 如图，矩形 $A B C D$ 中， $A B = 5 ， A D = 12$ ，点P在对角线 $B D$ 上，且 $B P = B A$ ，连接 $A P$ 并延长，交 $D C$ 的延长线于点Q，连接 $B Q$ ．

(1)、求证： $△ P D Q$ 是等腰三角形；

(2)、求 $C Q$ 和 $B Q$ 的长．

查看试题解析
25. 如图， $▱ A B C D$ 中， $A B = 3$ cm， $B C = 5$ cm， $∠ B = 60 °$ ， G是 $C D$ 的中点，E是边 $A D$ 上的动点， $E G$ 的延长线与 $B C$ 的延长线交于点F，连接 $C E$ ， $D F$ ．

(1)、求证：四边形 $C E D F$ 是平行四边形；

(2)、若四边形 $C E D F$ 是矩形，求 $A E$ 的长度；

(3)、当 $A E$ =cm时，四边形 $C E D F$ 是菱形．

查看试题解析