河北省邢台市2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-07-03 类型:期中考试
一、单选题
-
1. 正比例函数的比例系数为( )A、 B、 C、 D、22. 抽样调查放学时段,学校附近某路口车流量情况的样本中,下列最合适的是( )A、抽取一月份第一周为样本 B、抽取任意一天为样本 C、选取每周日为样本 D、每个季节各选两周作为样本3. 下列各点在一次函数的图像上的是( )A、 B、 C、 D、4. 统计的一般过程可以用下面框图所示的步骤进行,其中表示
 的是( )
的是( ) A、确定调查范围 B、设计调查选项 C、整理数据 D、选择调查方式5. 如图,在平面直角坐标系中有一点被墨迹遮挡了,这个点的坐标可能是( )
A、确定调查范围 B、设计调查选项 C、整理数据 D、选择调查方式5. 如图,在平面直角坐标系中有一点被墨迹遮挡了,这个点的坐标可能是( ) A、 B、 C、 D、6. 在函数中,自变量x的取值可以是( )A、0 B、2 C、4 D、87. 如图,把两根木条和的一端用螺栓固定在一起,木条自由转动至位置.在转动过程中,下面的量是常量的是( )
A、 B、 C、 D、6. 在函数中,自变量x的取值可以是( )A、0 B、2 C、4 D、87. 如图,把两根木条和的一端用螺栓固定在一起,木条自由转动至位置.在转动过程中,下面的量是常量的是( )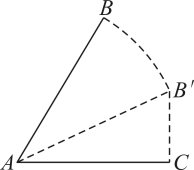 A、的度数 B、的面积 C、的长度 D、的长度8. 我国人口普查已经进行七次,人口普查采用普查方式的理由是( )A、人口调查的数目不太大 B、受条件限制,无法进行抽样调查 C、人口调查花费较少 D、人口调查需要获得全面准确的信息9. 对于下列曲线中,说法正确的是( )
A、的度数 B、的面积 C、的长度 D、的长度8. 我国人口普查已经进行七次,人口普查采用普查方式的理由是( )A、人口调查的数目不太大 B、受条件限制,无法进行抽样调查 C、人口调查花费较少 D、人口调查需要获得全面准确的信息9. 对于下列曲线中,说法正确的是( )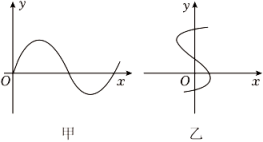 A、甲能表示y是x的函数 B、乙能表示y是x的函数 C、甲和乙均能表示y是x的函数 D、甲和乙均不能表示y是x的函数10. 在一次“寻宝”游戏中,寻宝人已经找到两个标志点和 , 并且知道藏宝地点的坐标是 , 则藏宝处应为图中的( )
A、甲能表示y是x的函数 B、乙能表示y是x的函数 C、甲和乙均能表示y是x的函数 D、甲和乙均不能表示y是x的函数10. 在一次“寻宝”游戏中,寻宝人已经找到两个标志点和 , 并且知道藏宝地点的坐标是 , 则藏宝处应为图中的( )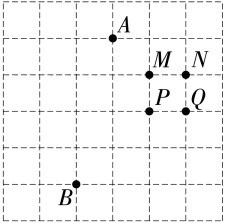 A、点 B、点 C、点 D、点11. 若 , 则一次函数的图象大致是( )A、
A、点 B、点 C、点 D、点11. 若 , 则一次函数的图象大致是( )A、 B、
B、 C、
C、 D、
D、 12. 一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干.设开始工作的时间为t,剩下的水量为s,下面能反映s与t之间的关系的大致图象是( )A、
12. 一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干.设开始工作的时间为t,剩下的水量为s,下面能反映s与t之间的关系的大致图象是( )A、 B、
B、 C、
C、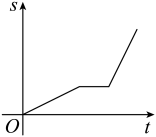 D、
D、 13. 已知在平面直角坐标系中, , , , , 则下列结论正确的是( )A、 B、 C、 D、14. 如图,在平面直角坐标系中有一个3×3的正方形网格,其右下角格点(小正方形的顶点)A的坐标为(﹣1,1),左上角格点B的坐标为(﹣4,4),若分布在过定点(﹣1,0)的直线y=﹣k(x+1)两侧的格点数相同,则k的取值可以是( )
13. 已知在平面直角坐标系中, , , , , 则下列结论正确的是( )A、 B、 C、 D、14. 如图,在平面直角坐标系中有一个3×3的正方形网格,其右下角格点(小正方形的顶点)A的坐标为(﹣1,1),左上角格点B的坐标为(﹣4,4),若分布在过定点(﹣1,0)的直线y=﹣k(x+1)两侧的格点数相同,则k的取值可以是( ) A、 B、 C、2 D、
A、 B、 C、2 D、二、填空题
-
15. 为了解某校七年级1000名学生每天的阅读时间,从中抽取了100名学生进行调查,在这个问题中,样本容量是 .16. 已知点 ,(1)、若点与点关于轴对称,则点纵坐标是 .(2)、若点与点关于原点对称,则 .17. 图(1),在中, , 点P从点A出发,沿三角形的以秒的速度运动,图(2)是点P运动时,线段的长度随运动时间x(秒)变化的关系图象.
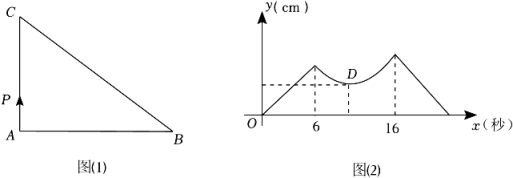 (1)、 , .(2)、若点D是曲线的最低点,则D的坐标为 .
(1)、 , .(2)、若点D是曲线的最低点,则D的坐标为 .三、解答题
-
18. 某电动车厂2022年各月份生产电动车的数量情况如表:
时间/月
1
2
3
4
5
6
7
8
9
10
11
12
月产量/万辆
8
8.5
9
10
11
12
10
9.5
9
10
10
10.5
(1)、在上述过程中,指出自变量和关于自变量的函数;(2)、哪个月份电动车的产量最高?哪个月份电动车的产量最低?19. 如图,是一个简单的平面示意图,已知 , , , 点为的中点,回答下列问题: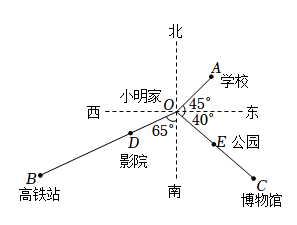 (1)、由图可知,高铁站在小明家南偏西方向处.请类似这种方法用方向与距离描述学校、博物馆相对于小明家的位置;(2)、图中到小明家距离相同的是哪些地方?20. 某校七年级开展了“勿忘历史,吾辈自强”历史知识竞赛活动,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表(每组成绩含前一个分数,不含后一个分数,最后一组前后分数均包含):
(1)、由图可知,高铁站在小明家南偏西方向处.请类似这种方法用方向与距离描述学校、博物馆相对于小明家的位置;(2)、图中到小明家距离相同的是哪些地方?20. 某校七年级开展了“勿忘历史,吾辈自强”历史知识竞赛活动,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表(每组成绩含前一个分数,不含后一个分数,最后一组前后分数均包含):
成绩/分
频数
百分比
第1段
50~60
2
4%
第2段
60~70
6
12%
第3段
70~80
9
b
第4段
80~90
a
36%
第5段
90~100
15
30%
请根据所给信息,解答下列问题
(1)、a= , b=;(2)、请补全频数分布直方图:(3)、现要将调查结果绘制成扇形统计图,求成绩在“90~100”这一分数段所对应的扇形圆心角是多少度?21. 图1所示,在平面直角坐标系中,为原点,点 , , . 将点向右平移7个单位长度,再向上平移4个单位长度,得到对应点 , 图2所示. (1)、求点坐标;(2)、连接、、 , 是一动点,若 , 请求出点的坐标.22. 图①、图②反映是东方百货商场今年月份的商品销售额统计情况.来自商场财务部的报告表明,商场月份的销售总额一共是万元,观察图①和图②,解答下面问题:
(1)、求点坐标;(2)、连接、、 , 是一动点,若 , 请求出点的坐标.22. 图①、图②反映是东方百货商场今年月份的商品销售额统计情况.来自商场财务部的报告表明,商场月份的销售总额一共是万元,观察图①和图②,解答下面问题:
 (1)、将图①补充完整;(2)、商场服装部5月份的销售额是多少万元?(3)、李强观察图②后认为,5月份服装部的销售额比4月份减少了.你同意他的看法吗?为什么?23. 如图,已知直线经过点、点 , 交轴于点 , 点是轴上一个动点,过点、作直线 .
(1)、将图①补充完整;(2)、商场服装部5月份的销售额是多少万元?(3)、李强观察图②后认为,5月份服装部的销售额比4月份减少了.你同意他的看法吗?为什么?23. 如图,已知直线经过点、点 , 交轴于点 , 点是轴上一个动点,过点、作直线 .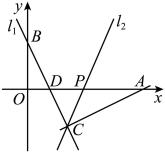 (1)、求直线的表达式;(2)、已知点 , 当时,求点的坐标;(3)、设点的横坐标为 , 点 , 是直线上任意两个点,若时, , 请直接写出的取值范围.24. 某工厂生产某种产品,每件产品的成本价为25元,出厂价为50元.在生产过程中,每件产品产生0.5立方米污水,工厂有两种方案对污水进行处理.
(1)、求直线的表达式;(2)、已知点 , 当时,求点的坐标;(3)、设点的横坐标为 , 点 , 是直线上任意两个点,若时, , 请直接写出的取值范围.24. 某工厂生产某种产品,每件产品的成本价为25元,出厂价为50元.在生产过程中,每件产品产生0.5立方米污水,工厂有两种方案对污水进行处理.方案1:自行处理,达标排放.每处理1立方米所用原料费2元,并且每月排污设备损耗费为30000元.
方案2:污水纳入污水处理厂统一处理,每处理1立方米污水需付14元的排污费.问:
(1)、设工厂每月生产x件产品,每月的利润为y元,分别求出按方案1,方案2处理污水时y与x的函数关系式;(2)、工厂每月生产多少件产品时,采用两种方案所获利润相同?请说明理由;(3)、工厂每月生产6000件产品时,采用何种方案才能使工厂所获利润最大?请通过计算加以说明.