山东省聊城市东阿县2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-07-03 类型:期中考试
一、单选题
-
1. 下列实数是无理数的是( )A、 B、 C、 D、2. 如图,数轴上的点与点所表示的数分别为 , , 则下列不等式不成立的是( )
 A、 B、 C、 D、3. 如图,是四边形的边延长线上的一点,且 , 则下列条件中不能判定四边形是平行四边形的是( )
A、 B、 C、 D、3. 如图,是四边形的边延长线上的一点,且 , 则下列条件中不能判定四边形是平行四边形的是( ) A、 B、 C、 D、4. 下列各式,没有意义的是( )A、 B、 C、 D、5. 如图,在矩形中, , , 在轴上,若以点为圆心,对角线的长为半径作弧,交轴的正半轴于点 , 则点的坐标为( )
A、 B、 C、 D、4. 下列各式,没有意义的是( )A、 B、 C、 D、5. 如图,在矩形中, , , 在轴上,若以点为圆心,对角线的长为半径作弧,交轴的正半轴于点 , 则点的坐标为( ) A、 B、 C、 D、6. 如图,在中,平分 , , 交边于点E,且 , 则的长为( )
A、 B、 C、 D、6. 如图,在中,平分 , , 交边于点E,且 , 则的长为( ) A、 B、3 C、4 D、57. 以下列各数为边长,能构成直角三角形的是( )A、1,2,2 B、1, ,2 C、4,5,6 D、1,1,8. 不等式组 的解集在数轴上用阴影表示正确的是( )A、
A、 B、3 C、4 D、57. 以下列各数为边长,能构成直角三角形的是( )A、1,2,2 B、1, ,2 C、4,5,6 D、1,1,8. 不等式组 的解集在数轴上用阴影表示正确的是( )A、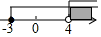 B、
B、 C、
C、 D、
D、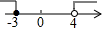 9. 如图,在中, , 分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”,当 , 时,则阴影部分的面积为( )
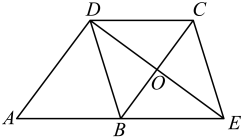
9. 如图,在中, , 分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”,当 , 时,则阴影部分的面积为( ) A、 B、 C、 D、910. 如图,在四边形中, , , . 分别以点A,C为圆心,大于长为半径作弧,两弧交于点E,作射线交于点F,交于点O.若点O是的中点,则的长为( )
A、 B、 C、 D、910. 如图,在四边形中, , , . 分别以点A,C为圆心,大于长为半径作弧,两弧交于点E,作射线交于点F,交于点O.若点O是的中点,则的长为( ) A、1 B、2 C、3 D、411. 某班人去科技馆参观,科技馆票价是每人10元,但若购团体票(不低于50张),则可享受八五折优惠.班长算了算,购买50张票反而更合算,则m至少为( )A、42 B、43 C、44 D、4512.
A、1 B、2 C、3 D、411. 某班人去科技馆参观,科技馆票价是每人10元,但若购团体票(不低于50张),则可享受八五折优惠.班长算了算,购买50张票反而更合算,则m至少为( )A、42 B、43 C、44 D、4512.如图,在Rt△ABC中,∠A=90°,P为边BC上一动点,PE⊥AB于E , PF⊥AC于F , 动点P从点B出发,沿着BC匀速向终点C运动,则线段EF的值大小变化情况是( ).
 A、一直增大 B、一直减小 C、先减小后增大 D、先增大后减少
A、一直增大 B、一直减小 C、先减小后增大 D、先增大后减少二、填空题
-
13. 在平行四边形ABCD中,比大 , 那么的度数为14. 如图,在中, , D,E,F分别为的中点.若的长为8,则的长为 .
 15. 定义新运算:对于任意实数a,b,都有 , 比如: . 若的值小于16,则满足条件的最小整数解为 .16. 若关于x的不等式组无解,则的取值范围是 .17. 如图,在直角坐标系中, , , 已知点的坐标为 , 点的坐标为 .
15. 定义新运算:对于任意实数a,b,都有 , 比如: . 若的值小于16,则满足条件的最小整数解为 .16. 若关于x的不等式组无解,则的取值范围是 .17. 如图,在直角坐标系中, , , 已知点的坐标为 , 点的坐标为 .
三、解答题
-
18. 计算:(1)、;(2)、 .19.(1)、解不等式:(2)、解不等式组: , 并写出它的整数解.20. 如图,在平行四边形中,E,F分别是 , 的中点,求证: .
 21. 如图,在中, , , 在中,是边上的高, , 的面积为60.
21. 如图,在中, , , 在中,是边上的高, , 的面积为60. (1)、求的长.(2)、求四边形的面积.22. 新时代中学名同学去工厂进行暑假实践活动,每名同学每天可以加工甲种零件个或乙种零件个,已知每加工一个甲种零件可获利元,每加工一个乙种零件可获利元,若要使车间每天获利不低于元,那加工甲种零件的同学至多为多少名?23. 已知的立方根是 , 的算术平方根是 , 是的整数部分.(1)、求 , , 的值;(2)、求的平方根.
(1)、求的长.(2)、求四边形的面积.22. 新时代中学名同学去工厂进行暑假实践活动,每名同学每天可以加工甲种零件个或乙种零件个,已知每加工一个甲种零件可获利元,每加工一个乙种零件可获利元,若要使车间每天获利不低于元,那加工甲种零件的同学至多为多少名?23. 已知的立方根是 , 的算术平方根是 , 是的整数部分.(1)、求 , , 的值;(2)、求的平方根.