山西省吕梁市交城县2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-07-03 类型:期中考试
一、单选题
-
1. 化简的正确结果是( )A、4 B、2 C、 D、2. 下列二次根式,化简后能与合并的是( )A、 B、 C、 D、3. 在中, , 则的面积为( )A、6 B、 C、10 D、204. 我国是最早了解勾股定理的国家之一.早在三千多年前,周朝数学家商高就提出了“勾三、股四、弦五”这一结论,被记载于我国古代一部著名的数学著作中.这部著作是( )A、《九章算术》 B、《周髀算经》 C、《孙子算经》 D、《海岛算经》5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,在平行四边形中, , 则的长为( )
 A、 B、 C、 D、7. 下列命题中正确的是( )A、平行四边形的对角线互相垂直 B、矩形的对角线相等 C、对角线相等的平行四边形是菱形 D、对角线互相垂直的平行四边形是正方形8. 已知 , 若是整数,则的值可能是( )A、 B、 C、 D、9. 如图是楼梯的示意图,楼梯的宽为5米,米,米,若在楼梯上铺设防滑材料,则所需防滑材料的面积至少为( )
A、 B、 C、 D、7. 下列命题中正确的是( )A、平行四边形的对角线互相垂直 B、矩形的对角线相等 C、对角线相等的平行四边形是菱形 D、对角线互相垂直的平行四边形是正方形8. 已知 , 若是整数,则的值可能是( )A、 B、 C、 D、9. 如图是楼梯的示意图,楼梯的宽为5米,米,米,若在楼梯上铺设防滑材料,则所需防滑材料的面积至少为( )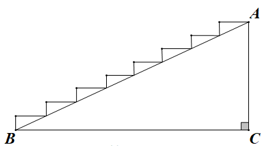 A、65 B、85 C、90 D、15010. 如图,点E是平行四边形的边的中点,连接并延长交的延长线于点F,连接 , 若 , 则四边形是( )
A、65 B、85 C、90 D、15010. 如图,点E是平行四边形的边的中点,连接并延长交的延长线于点F,连接 , 若 , 则四边形是( ) A、平行四边形 B、矩形 C、菱形 D、正方形
A、平行四边形 B、矩形 C、菱形 D、正方形二、填空题
-
11. 二次根式有意义,则实数的取值范围是 .12. 已知△ABC的三边长分别为 , , , 则的形状是 .13. 《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,则可列方程为(方程不用化简).
 14. 如图,在平行四边形中,对角线交于点O,交于点E,已知的周长为8, , 则的长为 .
14. 如图,在平行四边形中,对角线交于点O,交于点E,已知的周长为8, , 则的长为 . 15. 如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为 .
15. 如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为 .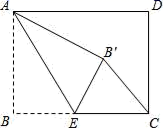
三、解答题
-
16. 计算:(1)、(2)、17. 已知三角形的三边 , , , 可以求出这个三角形的面积.古希腊几何学家海伦的公式为:(其中);我国南宋著名数学家秦九韶的公式为: . 若一个三角形的三边长分别是 , , , 求这个三角形的面积.(1)、你认为选择(填海伦公式或秦九韶公式)能使计算更简便;(2)、请利用你选择的公式计算出这个三角形的面积.18. 如图,在四边形中,平分 , , 点E是上一点, , 若 , , 求的长.
 19. 如图,在平行四边形中,点E是边上一点,且 , 的平分线交于点F,连接 .
19. 如图,在平行四边形中,点E是边上一点,且 , 的平分线交于点F,连接 . (1)、尺规作图:根据题意将图形补充完整(保留作图痕迹,不写做法,标注相应字母);(2)、求证:四边形是菱形.20. 如图,在矩形中,点E、点F分别是、的中点,连接 , , , , 与交于点G,与交于点H.
(1)、尺规作图:根据题意将图形补充完整(保留作图痕迹,不写做法,标注相应字母);(2)、求证:四边形是菱形.20. 如图,在矩形中,点E、点F分别是、的中点,连接 , , , , 与交于点G,与交于点H. (1)、求证:四边形是平行四边形;(2)、请判断四边形的形状,并说明理由.21. 按要求作图:下面三幅网格图中的小正方形的边长都为1,每个小正方形的顶点称为格点.
(1)、求证:四边形是平行四边形;(2)、请判断四边形的形状,并说明理由.21. 按要求作图:下面三幅网格图中的小正方形的边长都为1,每个小正方形的顶点称为格点.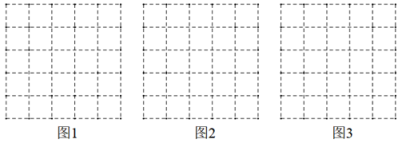 (1)、在图1中作一个边长都为整数的格点直角三角形;(2)、在图2中作一个边长分别为 , , 的格点三角形;(3)、在图3中作一个有一边长为的格点平行四边形 .(4)、请判断图2中所作的形状,并说明理由.22. 问题情境:
(1)、在图1中作一个边长都为整数的格点直角三角形;(2)、在图2中作一个边长分别为 , , 的格点三角形;(3)、在图3中作一个有一边长为的格点平行四边形 .(4)、请判断图2中所作的形状,并说明理由.22. 问题情境:勾股定理是一个古老的数学定理,它有很多种证明方法.下面利用拼图的方法探究证明勾股定理.
(1)、定理表述:请你结合图1中的直角三角形,叙述勾股定理(可以选择文字语言或符号语言叙述);
 (2)、尝试证明:
(2)、尝试证明:利用图1中的直角三角形可以构造出如图2的直角梯形,请你利用图2证明勾股定理.
 (3)、定理应用:
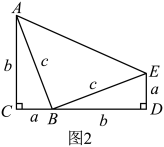
(3)、定理应用:某工程队要从点A向点E铺设管道,由于受条件限制无法直接沿着线段铺设,需要绕道沿着矩形的边和铺设管道,经过测量米,米,已知铺设每米管道需资金1000元,请你帮助工程队计算绕道后费用增加了多少元?
 23. 如图1,四边形是菱形,点E,点F分别是 , 边上的动点, , 连接 , 交对角线于点G,H.
23. 如图1,四边形是菱形,点E,点F分别是 , 边上的动点, , 连接 , 交对角线于点G,H.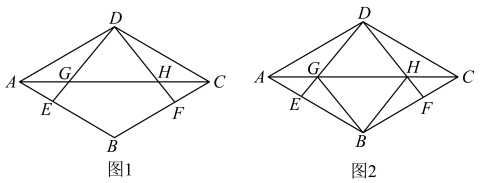 (1)、求证:;(2)、如图2,连接 , , 请判断四边形是什么特殊四边形?并说明你的理由;(3)、在图2中,如果 , , 试探究在点E,F运动过程中,如果四边形成为正方形,则的长度是多少?(请直接写出答案)
(1)、求证:;(2)、如图2,连接 , , 请判断四边形是什么特殊四边形?并说明你的理由;(3)、在图2中,如果 , , 试探究在点E,F运动过程中,如果四边形成为正方形,则的长度是多少?(请直接写出答案)