山西省吕梁市孝义市2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-07-03 类型:期中考试
一、单选题
-
1. 若二次根式在实数范围内有意义,则a的取值范围是( )A、 B、 C、 D、2. 下列二次根式中,可以与合并的是( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 下列各组数中不能作为直角三角形三边长的是( )A、 , , B、 , , C、 , , D、 , ,5. 如图,在中, , 在数轴上,点所表示的数为1,以点为圆心,长为半径画弧,在点左侧交数轴于点 , 则点表示的数是( )
 A、 B、 C、 D、6. 如图,在中,对角线相交于点 , 过点作交于点 , 连接 . 若的周长为20,则的周长为( )
A、 B、 C、 D、6. 如图,在中,对角线相交于点 , 过点作交于点 , 连接 . 若的周长为20,则的周长为( ) A、5 B、10 C、15 D、207. 在学习平行四边形时,我们先学习了平行四边形的性质定理、判定定理,再通过平行四边形边、角的特殊化,获得了特殊的平行四边形——矩形、菱形和正方形,了解了它们之间的关系,并根据它们的特殊性,得到了这些特殊的平行四边形的性质定理和判定定理.在学习这些知识的过程中,主要体现的数学思想是( )A、方程思想 B、数形结合思想 C、从特殊到一般思想 D、从一般到特殊思想8. 如图,在矩形中,对角线相交于点 , , , , 若四边形的周长为12,则的长为( )
A、5 B、10 C、15 D、207. 在学习平行四边形时,我们先学习了平行四边形的性质定理、判定定理,再通过平行四边形边、角的特殊化,获得了特殊的平行四边形——矩形、菱形和正方形,了解了它们之间的关系,并根据它们的特殊性,得到了这些特殊的平行四边形的性质定理和判定定理.在学习这些知识的过程中,主要体现的数学思想是( )A、方程思想 B、数形结合思想 C、从特殊到一般思想 D、从一般到特殊思想8. 如图,在矩形中,对角线相交于点 , , , , 若四边形的周长为12,则的长为( ) A、3 B、6 C、 D、9. 如图,依次连接周长为1的小等边三角形各边的中点,得到第二个小等边三角形,再依次连接第二个小等边三角形各边的中点,得到第三个小等边三角形……按这样的规律,第2023个小等边三角形的周长为( )
A、3 B、6 C、 D、9. 如图,依次连接周长为1的小等边三角形各边的中点,得到第二个小等边三角形,再依次连接第二个小等边三角形各边的中点,得到第三个小等边三角形……按这样的规律,第2023个小等边三角形的周长为( ) A、 B、 C、 D、10. 宽与长的比是(约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,我们可以折叠出一个黄金矩形.第一步,在一张矩形纸片的一端利用图1的方法折出一个正方形,然后把纸片展平;第二步,如图2,把这个正方形折成两个相等的矩形,再把纸片展平,折痕是;第三步,折出内侧矩形的对角线 , 并把折到图3中所示的处,折痕为;第四步,如图4,展平纸片,按照所得的点折出 , 使 . 则下列是黄金矩形的是( )
A、 B、 C、 D、10. 宽与长的比是(约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,我们可以折叠出一个黄金矩形.第一步,在一张矩形纸片的一端利用图1的方法折出一个正方形,然后把纸片展平;第二步,如图2,把这个正方形折成两个相等的矩形,再把纸片展平,折痕是;第三步,折出内侧矩形的对角线 , 并把折到图3中所示的处,折痕为;第四步,如图4,展平纸片,按照所得的点折出 , 使 . 则下列是黄金矩形的是( ) A、矩形 B、矩形 C、矩形 D、矩形
A、矩形 B、矩形 C、矩形 D、矩形二、填空题
-
11. 如图,菱形的对角线与交于点 , 请你添加一个条件使它是正方形,你添加的条件是
 12. 在没有直角工具之前,聪明的古埃及人用如图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中5这条边所对的角便是直角.依据是 .
12. 在没有直角工具之前,聪明的古埃及人用如图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中5这条边所对的角便是直角.依据是 . 13. 电流通过导线时会产生热量,电流I(单位:A)、导线电阻R(单位:)、通电时间t(单位:s)与产生的热量Q(单位:J)满足 . 已知导线的电阻为9 , 1s时间导线产生72J的热量,则电流的值是A.14. 如图,点O是矩形ABCD的对角线AC的中点,M是AD的中点,若OM=3,BC=8,则OB的长为 。
13. 电流通过导线时会产生热量,电流I(单位:A)、导线电阻R(单位:)、通电时间t(单位:s)与产生的热量Q(单位:J)满足 . 已知导线的电阻为9 , 1s时间导线产生72J的热量,则电流的值是A.14. 如图,点O是矩形ABCD的对角线AC的中点,M是AD的中点,若OM=3,BC=8,则OB的长为 。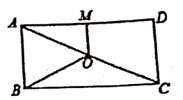 15. 如图,菱形的边长为4, , 点是边的中点,点是对角线上一动点,则周长的最小值是 .
15. 如图,菱形的边长为4, , 点是边的中点,点是对角线上一动点,则周长的最小值是 .
三、解答题
-
16. 计算(1)、(2)、17. 已知 , , 求的值.18. 如图,在边长均为1的小正方形网格中,线段的端点都在格点上.(小正方形的顶点叫格点.)
实践与操作:
以为一边作正方形;(点C,D画在格点上)
推理与计算:
线段的长为 ▲ ,正方形的面积为 ▲ .
 19. 如图,的对角线交于点 , 点分别是的中点,依次连接 . 求证:四边形是平行四边形.
19. 如图,的对角线交于点 , 点分别是的中点,依次连接 . 求证:四边形是平行四边形. 20. 某校“综合与实践”小组开展了测量本校旗杆高度的实践活动.他们制订了测量方案,并利用课余时间完成了实地测量,测量结果如下表(不完整).
20. 某校“综合与实践”小组开展了测量本校旗杆高度的实践活动.他们制订了测量方案,并利用课余时间完成了实地测量,测量结果如下表(不完整).课题
测量学校旗杆的高度
成员
组长: 组员: , ,
工具
皮尺等
测量示意图

说明:线段AB表示学校旗杆,垂直地面于点B,如图1,第一次将系在旗杆顶端的绳子垂直到地面,并多出了一段BC,用皮尺测出的长度;如图2,第二次将绳子拉直,绳子末端落在地面的点D处,用皮尺测出的距离.
测量数据
测量项目
数值
图1中的长度
1米
图2中的长度
米
…
…
(1)、根据以上测量结果,请你帮助该“综合与实践”小组求出学校旗杆的高度.(2)、该小组要写出一份完整的课题活动报告,除上表的项目外,你认为还需要补充哪些项目(写出一个即可).21. 请阅读下列材料,并完成相应任务.勾股定理的证明
勾股定理揭示了直角三角形三条边之间的数量关系,是数学中最重要的定理之一. 勾股定理的证明过程多数采用的方法是“用两种不同的方法和含有a,b,c的式子表示同一个图形的面积”,由于同一个图形的面积相等,从而得到含a,b,c的恒等式,通过化简即可完成勾股定理的证明.借助于图形的面积研究相关的数量关系,是我国古代数学研究中经常采用的重要方法,它充分显示了古人的卓越智慧.
下面是证明勾股定理的一种思路:
如图,用一个等腰直角三角形(),和两个全等的直角三角形()可以拼成一个直角梯形 . 其中; , 用两种不同的方法和含有a,b,c的式子表示梯形的面积,就能完成勾股定理的证明.
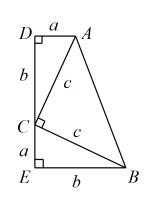
提示:梯形的面积(上底+下底)高
任务:
(1)、请你根据上述材料中的思路证明勾股定理;(2)、如图,在菱形中,对角线相交于点O, , 则之间的距离为 .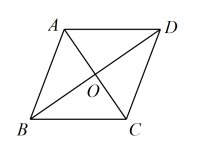 22. 综合与实践
22. 综合与实践实践操作:如图1,已知矩形纸片 .
第一步:如图2,将纸片沿折叠,使点B的对应点正好落在上,然后展平纸片,得到折痕;
第二步:如图3,在图2的基础上,沿折叠纸片,点C的对应点落在处,与交于点F.

问题解决:
(1)、如图2,判断四边形的形状,并证明;(2)、如图3,证明;(3)、若 , 则的周长为(直接写出答案即可).