天津市河东区2022-2023学年八年级下学期数学期中考试试卷

试卷更新日期：2023-07-03 类型：期中考试

进入出卷网下载

一、单选题

1. 若式子 $\sqrt{x - 3}$ 在实数范围内有意义，则x的取值范围是（）

A、x≥3 B、x≤3 C、x＞3 D、x＜3

查看试题解析
2. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{5}$ B、 $\sqrt{4}$ C、 $\sqrt{12}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
3. 如果下列各组数是三角形的三边，那么不能组成直角三角形的一组数是（）

A、2，3，4 B、3，4，5 C、6，8，10 D、5，12，13

查看试题解析
4. 如图，数轴的原点为O，点A在数轴上表示的数是2， $A B = 1$ ，且 $A B ⊥ O A$ ，以点O为圆心， $O B$ 长为半径画弧，交数轴于点C，则点C表示的数是（　　）

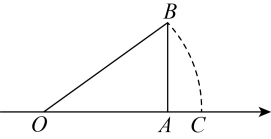A、 $\frac{5}{2}$ B、 $\frac{\sqrt{3}}{2} + 1$ C、 $\sqrt{5}$ D、 $\sqrt{2} + 1$

查看试题解析
5. 下列计算正确的是（　　）

A、 $\sqrt{2} \cdot \sqrt{3} = \sqrt{5}$ B、 $4 \sqrt{3} - 3 \sqrt{3} = 1$ C、 $2 \sqrt{3} \times 3 \sqrt{3} = 18$ D、 $\sqrt{27} \div \sqrt{3} = \sqrt{3}$

查看试题解析
6. 如图，在平行四边形ABCD中，∠A＋∠C＝160°，则∠B的度数是（）

A、130° B、120° C、100° D、90°

查看试题解析
7. 已知 $\sqrt{24 n}$ 是整数，则正整数n的最小值是（）

A、2 B、4 C、6 D、8

查看试题解析
8. 数学中有一些命题的特征是：原命题是真命题，但它的逆命题却是假命题．例如：如果a＞2，那么a²＞4．下列命题中，具有以上特征的命题是（）

A、两直线平行，同位角相等 B、如果|a|＝1，那么a＝1 C、全等三角形的对应角相等 D、如果x＞y ，那么mx＞my

查看试题解析
9. 四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）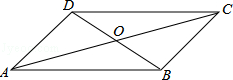

A、AB//DC，AD//BC B、AB=DC，AD=BC C、AO=CO，BO=DO D、AB//DC，AD=BC

查看试题解析
10.
已知，如图，一轮船以16海里/时的速度从港口A出发向东北方向航行，另一轮船以12海里/时的速度同时从港口A出发向东南方向航行，离开港口2小时后，则两船相距（）

A、25海里 B、30海里 C、35海里 D、40海里

查看试题解析
11. 如图，在四边形ABCD中，AB=CD，M，N，P分别是AD，BC，BD的中点，若∠MPN=130°，则∠NMP的度数为（）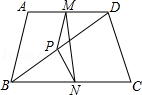

A、10° B、15° C、25° D、40°

查看试题解析
12. 如图，RtΔABC中，AB=9，BC=6，∠B=90°，将ΔABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（）

A、 $\frac{5}{3}$ B、 $\frac{5}{2}$ C、4 D、5

查看试题解析

二、填空题

13. 将 $\sqrt{12}$ 化为最简根式是.

查看试题解析
14. 如图，已知在 $△ A B C$ 中，D、E分别是 $A B$ 、 $A C$ 的中点， $B C = 16 c m$ ，则 $D E$ 的长度是cm．

查看试题解析
15. 若a，b都是实数，b＝ $\sqrt{1 - 2 a}$ + $\sqrt{2 a - 1}$ ﹣2，则a^b的值为.

查看试题解析
16. 如图，在平行四边形 $A B C D$ 中， $A B = 3$ ， $B C = 5$ ， $∠ B$ 的平分线 $B E$ 交 $A D$ 于点E，则 $D E$ 的长为．

查看试题解析
17. 化简 ${(\sqrt{3} - 2)}^{2019} \times {(\sqrt{3} + 2)}^{2020}$ 的结果为．

查看试题解析
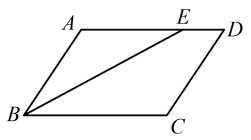18. 如图，△ABC是边长为1的等边三角形，取BC边中点E，作ED∥AB，EF∥AC，得到四边形EDAF，它的周长记作C₁；取BE中点E₁ ，作E₁D₁∥FB，E₁F₁∥EF，得到四边形E₁D₁FF₁ ，它的周长记作C₂ ．照此规律作下去，则C₂₀₂₀＝__．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{18} - \sqrt{32} + \sqrt{2}$ ；

(2)、 $2 \sqrt{12} \times \frac{\sqrt{3}}{4} \div 5 \sqrt{2}$ ．

查看试题解析
20. 已知 $a = 2 \sqrt{3} + 3 \sqrt{2} ， b = 2 \sqrt{3} - 3 \sqrt{2}$ ，求下列各式的值

(1)、 $a \cdot b$

(2)、 $a^{2} - b^{2}$

查看试题解析
21. 在Rt△ABC中，∠C=90°．

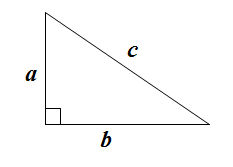(1)、若a=b=5，求c；

(2)、若a=5，∠A=30°，求b，c．

查看试题解析
22. 如图，已知平行四边形ABCD，AC、BD相交于点O，AB=4，AC=6，BD=10．

(1)、求∠ACD的度数；

(2)、求BC的长.

查看试题解析
23. 如图，在平行四边形 $A B C D$ 中，E，F分别是 $A D$ ， $B C$ 边上的点， $D E = C F$ ，连接 $B E$ 和 $A F$ 的交点为M， $C E$ 和 $D F$ 的交点为N，连接 $M N$ ， $E F$ ．

(1)、求证：四边形 $A B F E$ 为平行四边形．

(2)、若 $A D = 6 c m$ ，求 $M N$ 的长．

查看试题解析
24. 如图，已知 $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 8 c m$ ， $B C = 6 c m$ ．

(1)、若 $P$ 、 $Q$ 是 $△ A B C$ 边上的两个动点，其中点 $P$ 从 $A$ 沿 $A$ → $B$ 方向运动，速度为每秒 $1 c m$ ，点 $Q$ 从 $B$ 沿 $B$ → $C$ 方向运动，速度为每秒 $2 c m$ ，两点同时出发，设出发时间为 $t$ 秒．①当 $t = 1$ 秒时，求 $P Q$ 的长；②从出发几秒钟后， $△ P Q B$ 是等腰三角形？

(2)、若 $M$ 在 $△ A B C$ 边上沿 $B$ → $A$ → $C$ 方向以每秒 $3 c m$ 的速度运动，则当点 $M$ 在边 $C A$ 上运动时，求 $△ B C M$ 成为等腰三角形时 $M$ 运动的时间．

查看试题解析