天津市北辰区第三学区2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-07-03 类型:期中考试
一、单选题
-
1. 若式子在实数范围内有意义,则实数的取值范围是( )A、 B、 C、 D、2. 下列二次根式中,不能与合并的是( )A、 B、 C、 D、3. 等于( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 以下列线段为边,不能组成直角三角的是( )A、 , , B、1,2, C、3,4,5 D、5,12,136. 菱形具有而矩形不一定具有的性质是( )A、对角线相等 B、对角线平分对角 C、对角线互相平分 D、对角相等7. 若 , 则的值为( )A、1 B、 C、3 D、8. 如图,垂直地面的旗杆在离地3m处断裂,旗杆顶部落地点离旗杆底部4m,则旗杆折断前的高度为( )
 A、6 B、7 C、8 D、99. 如图,在平行四边形中,与相交于点O,那么图中的全等三角形共有( )
A、6 B、7 C、8 D、99. 如图,在平行四边形中,与相交于点O,那么图中的全等三角形共有( ) A、1对 B、2对 C、4对 D、6对10. 如图,将一个长为10cm,宽为8cm的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )
A、1对 B、2对 C、4对 D、6对10. 如图,将一个长为10cm,宽为8cm的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( ) A、10 cm2 B、20 cm2 C、40 cm2 D、80 cm211. 如图,▱ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
A、10 cm2 B、20 cm2 C、40 cm2 D、80 cm211. 如图,▱ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )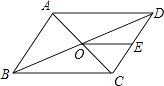 A、15 B、18 C、21 D、2412. 如图,将正方形纸片折叠,使边均落在对角线上,得折痕 , 则的度数是( )
A、15 B、18 C、21 D、2412. 如图,将正方形纸片折叠,使边均落在对角线上,得折痕 , 则的度数是( ) A、 B、 C、 D、13. 如图,矩形ABCD的对角线相交于点O,AE平分∠BAD交BC于E, 若∠CAE=15°则∠BOE=( )
A、 B、 C、 D、13. 如图,矩形ABCD的对角线相交于点O,AE平分∠BAD交BC于E, 若∠CAE=15°则∠BOE=( ) A、30° B、45° C、60° D、75°14. 如图,在 中, , ,按以下步骤作图:①以点 为圆心,以 长为半径作弧,交 于点 ;②分别以点 , 为圆心,以 长为半径作弧,两弧相交于点 ,作射线 交 于点 ,则 的长为( )
A、30° B、45° C、60° D、75°14. 如图,在 中, , ,按以下步骤作图:①以点 为圆心,以 长为半径作弧,交 于点 ;②分别以点 , 为圆心,以 长为半径作弧,两弧相交于点 ,作射线 交 于点 ,则 的长为( )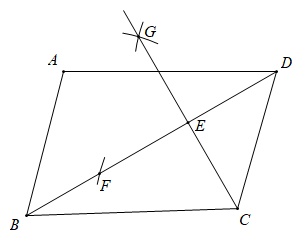 A、3 B、 C、4 D、15. 如图每个小正方形的边长为 , 在中,点分别为的中点,则线段的长为( )
A、3 B、 C、4 D、15. 如图每个小正方形的边长为 , 在中,点分别为的中点,则线段的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
16. 计算:= .
17. 计算: =.18. 在中, , 则的周长为 .19. 如图:在中, , , , 则的长是 . 20. 如图,菱形ABCD的对角线AC,BD相交于点O,E为DC的中点,若 , 则菱形的周长为 .
20. 如图,菱形ABCD的对角线AC,BD相交于点O,E为DC的中点,若 , 则菱形的周长为 . 21. 正方形的边长为 , 点分别是对角线上的两点,过点分别作的平行线,则图中阴影部分的面积等于 .
21. 正方形的边长为 , 点分别是对角线上的两点,过点分别作的平行线,则图中阴影部分的面积等于 . 22. 如图,数字代表所在正方形的面积,则A所代表的正方形的面积为 .
22. 如图,数字代表所在正方形的面积,则A所代表的正方形的面积为 . 23. 点在正方形外,是等边三角形,则 .
23. 点在正方形外,是等边三角形,则 . 24. 如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为 .
24. 如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为 .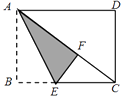 25. 如图,在边长为4的正方形中,点为的中点,为对角线上的一个动点,则的最小值的是 .
25. 如图,在边长为4的正方形中,点为的中点,为对角线上的一个动点,则的最小值的是 .
三、解答题
-
26. 计算下列各题(1)、(2)、(3)、(4)、27. 如图,四边形是菱形, , . 求:
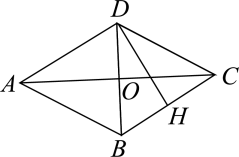 (1)、的度数和、的长.(2)、 , 求的长.28. 如图梯子斜靠在竖直的墙 , 长为 , 为 .
(1)、的度数和、的长.(2)、 , 求的长.28. 如图梯子斜靠在竖直的墙 , 长为 , 为 . (1)、求梯子的长.(2)、梯子的顶端A沿墙下滑到点C,梯子底端B外移到点D,求的长.
(1)、求梯子的长.(2)、梯子的顶端A沿墙下滑到点C,梯子底端B外移到点D,求的长.

