（冀教版）2023-2024学年九年级数学上册24.4 一元二次方程的应用期中复习

试卷更新日期：2023-07-03 类型：复习试卷

进入出卷网下载

一、选择题

1. “读万卷书，行万里路.”某校为了丰富学生的阅历知识，坚持开展课外阅读活动，学生人均阅读量从七年级的每年100万字增加到九年级的每年121万字.设该校七至九年级人均阅读量年均增长率为x，则可列方程为（）

A、 $100 {(1 + x)}^{2} ＝ 121$ B、 $100 {(1 + x %)}^{2} ＝ 121$ C、 $100 (1 + 2 x) ＝ 121$ D、 $100 + 100 (1 + x) + 100 {(1 + x)}^{2} ＝ 121$

查看试题解析
2. 新冠肺炎是一种传染性极强的疾病，如果有一人患病，经过两轮传染后有64人患病，设每轮传染中平均一个人传染了x个人，下列列式正确的是（）

A、 $x + x (1 + x) = 64$ B、 $1 + x + x^{2} = 64$ C、 $(1 + x)^{2} = 64$ D、 $x (1 + x) = 64$

查看试题解析
3. 我国快递业务逐年增加，2019年至2021年我国快递业务收入由7500亿元增加到9000亿元.设我国2019年至2021年快递业务收入的年平均增长率为x ，则可列方程为（　　）

A、 $7500 (1 + 2 x) = 9000$ B、 $7500 \times 2 (1 + x) = 9000$ C、 $7500 {(1 + x)}^{2} = 9000$ D、 $7500 + 7500 (1 + x) + 7500 {(1 + x)}^{2} = 9000$

查看试题解析
4. 某市某鞋厂10月份的运动鞋产量为24万双，因销量较好，11月份、12月份均增大产量，使第四季度的总产量达到88万双设该厂11、12月份的运动鞋产量的月平均增长率为x，根据题意可列方程为（）

A、 $88 {(1 + x)}^{2} = 24$ B、 $88 {(1 - x)}^{2} = 24$ C、 $24 {(1 + x)}^{2} = 88$ D、 $24 + 24 (1 + x) + 24 {(1 + x)}^{2} = 88$

查看试题解析
5. 为促进消费，成都市政府开展发放政府补贴消费的“消费券活动”，某商场的月销售额逐步增加.据统计8月份的销售额为200万元，接下来9月，10月的月增长率相同，10月份的销售额为500万元，若设9月，10月每月的增长率为 $x$ ，则可列方程为（）

A、 $200 (1 + x) = 500$ B、 $200 + 200 (1 + x) = 500$ C、 $200 {(1 + x)}^{2} = 500$ D、 $200 (1 + 2 x) = 500$

查看试题解析
6. 某超市购进一批商品，单价40元．经市场调查，销售定价为52元时，可售出180个，定价每增加1元，销售量减少10个，因受库存的影响，每批次进货个数不得超过180个，超市若将准备获利2000元，则定价为多少元？（）

A、50 B、60 C、50或60 D、100

查看试题解析
7. 九（1）班毕业时，每一个同学都将自己的照片向全班其他同学各送一张作为留念，全班共送了1560张照片，如果全班有x名学生，根据题意可列方程为（）

A、 $x (x - 1) = 1560$ B、 $x (x + 1) = 1560$ C、 $2 x (x + 1) = 1560$ D、 $2 x (x - 1) = 1560$

查看试题解析
8. 受国际油价影响，今年我国汽油价格总体呈上升趋势.已知某地92号汽油价格三月底是6.2元/升，五月底是8.9元/升.设该地92号汽油价格这两个月平均每月的增长率为 $x$ ，根据题意列出方程，正确的是（）

A、 $6.2 {(1 + x)}^{2} = 8.9$ B、 $8.9 {(1 + x)}^{2} = 6.2$ C、 $6.2 (1 + x^{2}) = 8.9$ D、 $6.2 (1 + x) + 6.2 {(1 + x)}^{2} = 8.9$

查看试题解析
9. 有一人患了流感，经过两轮传染后共有121人患了流感，每轮传染中平均一个人传染了几个人？设每轮传染中平均一个人传染了x个人，下列所列方程正确的是（）

A、 ${(1 + x)}^{2} = 121$ B、 $1 + x + x^{2} = 121$ C、 $1 + x + {(x + 1)}^{2} = 121$ D、 $1 + x + 2 (x + 1) = 121$

查看试题解析
10. 某公司前年缴税40万元，今年缴税48.4万元，求该公司这两年缴税的年平均增长率为多少．设该公司这两年缴税的年平均增长率为x，根据题意，下列所列的方程正确的是（）

A、 $40 {(1 + x)}^{2} = 48.4$ B、 $40 (1 + x^{2}) = 48.4$ C、 $48.4 {(1 - x)}^{2} = 40$ D、 $40 + 40 (1 + x) + 40 {(1 + x)}^{2} = 48.4$

查看试题解析

二、填空题

11. 有1个人患了流感，经过两轮传染后共有36人患了流感，那么平均每轮传染人.

查看试题解析
12. 梭梭树因其顽强的生命力和防风固沙的作用，被称为“沙漠植被之王”．新疆北部某沙漠2020年有16万亩梭梭树，经过两年的人工种植和自然繁殖，2022年达到25万亩，求这两年的平均增长率．

查看试题解析
13. 如图，用120米长的围网围建一个面积为560平方米的矩形养殖场．为了节省材料，养殖场的一边靠墙（墙足够长），并在如图的两个位置各开出一个1米宽的门（门不用围网做）．设矩形AB边长为x米，请依题意列方程：．

查看试题解析
14. 电影《长津湖之水门桥》讲述了一段波澜壮阔的历史，一上映就获得全国人民的追捧，某地第一天票房约2亿元，以后每天票房按相同的增长率增长，第三天票房收入达2.88亿元，若把增长率记作x，则方程可以列为.

查看试题解析
15. 某机械厂七月份生产零件50万个，第三季度生产零件196万个．设该厂八、九月份平均每月的增长率为x，那么方程是．

查看试题解析

三、解答题

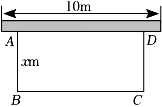
16. 如图，某农场计划建造一个矩形养殖场，为充分利用现有资源，该矩形养殖场一面靠墙（墙的长度为 $10 m$ ），另外三面用栅栏围成，已知栅栏总长度为 $18 m$ ，设矩形垂直于墙的一边，即 $A B$ 的长为 $x m$ .若矩形养殖场的面积为 $36 m^{2}$ ，求此时的x的值.

查看试题解析
17. 某商店以每个8元的成本价购进了一批玩具陀螺，如果以每个14元的价格出售，那么每天可销售40个，经市场调查发现，若每个陀螺的售价每上涨1元，则每天的销售量就减少2个.每个陀螺涨价多少元时，才能让顾客得到实惠的同时商店每天获得的利润为320元？

查看试题解析
18. 疫情期间“停课不停学”，辽宁省初中数学学科开通公众号进行公益授课，9月份该公众号关注人数为5000人，11月份该公众号关注人数达到7200人，若从9月份到11月份，每月该公众号关注人数的平均增长率相同，求该公众号关注人数的月平均增长率．

查看试题解析

19. 根据以下素材，探索完成任务

如何设计纸盒
素材1	利用一边长为40cm的正方形纸板可能设计成如图1和图2所示的两种纸盒，图1是无盖的纸盒，图2是一个有盖的纸盒.
素材2	如图，若在正方形硬纸板的四角各剪掉一个同样大小的小正方形，将剩余部分折成一个无盖的长方体盒子。
问题解决
任务1	初步探究：折一个底面积为 $484 c m^{2}$ 无盖长方体盒子	求剪掉的小正方形的边长为多少？
任务2	探究折成的无盖长方体盒子的侧面积是否有最大值？	如果有，求出这个最大值和此时剪掉的小正方形的边长；如果没有，说明理由

查看试题解析

四、综合题

20. 某大型批发商场平均每天可售出某款商品3000件，售出1件该款商品的利润是10元. 经调查发现，若该款商品的批发价每降低1元，则每天可多售出1000件.为了使每天获得的利润更多，该批发商场决定降价x元销售该款商品.

(1)、当x为多少元时，该批发商场每天卖出该款商品的利润为40000元？

(2)、若按照这种降价促销的策略，该批发商场每天卖出该款商品的利润能达50000元吗？若能，请求出x的值，若不能，请说明理由.

查看试题解析
21. 某市从2020年起连续投入资金用于 $“$ 建设美丽城市，改造老旧小区 $”$ .已知每年投入资金的增长率相同，其中2020年投入资金1000万元，2020年投入资金1440万元.

(1)、求该市改造老旧小区投入资金的年平均增长率；

(2)、2022年老旧小区改造的平均费用为每个80万元.2023年为提高老旧小区品质，每个小区改造费用计划增加20%.如果投入资金年增长率保持不变，求该市2023年最多可以改造多少个老旧小区？

查看试题解析
22. 2022成都世乒赛期间，某店直接从工厂购进A、B两款纪念品，进货价和销售价如下表：（注：利润 $=$ 销售价 $-$ 进货价）
类别价格
A款纪念品
B款纪念品
进货价（元/件）
20
15
销售价（元/件）
35
27

(1)、该店第一次用850元购进A、B款纪念品共50件，求两款纪念品分别购进的件数；

(2)、第一次购进的纪念品售完后，该网店计划再次购进A、B两款纪念品共200件（进货价和销售价都不变），且进货总价不高于3200元，应如何设计进货方案，才能获得最大销售利润，最大销售利润是多少?

(3)、成都世乒赛临近结束时，网店打算把B款纪念品调价销售.如果按照原价销售，平均每天可售4件，经调查发现，每降价1元，平均每天可多售2件，将销售价定为每件多少元时，才能使B款纪念品平均每天销售利润为90元？

查看试题解析
23. 2013年，东营市某楼盘以每平方米6500元的均价对外销售．因为楼盘滞销，房地产开发商为了加快资金周转，决定进行降价促销，经过连续两年下调后，2015年的均价为每平方米5265元．

(1)、求平均每年下调的百分率；

(2)、假设2016年的均价仍然下调相同的百分率，张强准备购买一套100平方米的住房，他持有现金20万元，可以在银行贷款30万元，张强的愿望能否实现？（房价每平方米按照均价计算）

查看试题解析

类别价格	A款纪念品	B款纪念品
进货价（元/件）	20	15
销售价（元/件）	35	27

（冀教版）2023-2024学年九年级数学上册24.4 一元二次方程的应用 期中复习

一、选择题

二、填空题

三、解答题

四、综合题

（冀教版）2023-2024学年九年级数学上册24.4 一元二次方程的应用期中复习