(冀教版)2023-2024学年九年级数学上册24.3 一元二次方程根与系数的关系 期中复习
试卷更新日期:2023-07-03 类型:复习试卷
一、选择题
-
1. 已知a,b是一元二次方程的两根,则的值是( )A、2 B、 C、 D、-22. 已知一元二次方程有两个实数根 , 则的值为( )A、6 B、2 C、4 D、33. 设a,b是方程的两个实数根,则的值为( )A、2019 B、2020 C、2021 D、20224. 已知、是关于x的方程的两根,下列结论中不一定正确的是( )A、 B、 C、 D、方程的根有可能为05. 若方程的两个根,则( )A、2 B、-2 C、3 D、-36. 若m、n是一元二次方程的两个实数根,则的值为( )A、1 B、-1 C、2 D、-27. 若关于x的方程x2+2mx+m2+3m-2=0有两个实数根x1、x2 , 则x1(x2+x1)+x22的最小值为 ( )A、 B、 C、 D、-28. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2)和(0,3)两点之间(包含端点).下列结论中正确的是( )
①不等式ax2+c<-bx的解集为x<-1或x>3;②9a2-b2<0;③一元二次方程cx2+bx+a=0的两个根分别为x1=
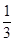 ,x2=-1;④6≤3n-2≤10.
,x2=-1;④6≤3n-2≤10.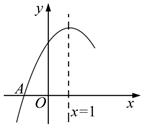 A、①②③ B、①②④ C、②③④ D、①③④9. 如图,函数的图象过点和 , 请思考下列判断:
A、①②③ B、①②④ C、②③④ D、①③④9. 如图,函数的图象过点和 , 请思考下列判断: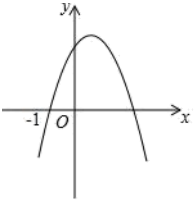
①;②;③;④;⑤.
正确的是( )
A、①③⑤ B、①③④ C、①②③④⑤ D、①②③⑤10. 平面直角坐标系中,抛物线y=ax2-3ax+c(a≠0)与直线y=2x+1上有三个不同的点A(x1 , m),B(x2 , m),C(x3 , m),如果n=x1+x2+x3 , 那么m和n的关系是( )A、m=2n-3 B、m=n2-3 C、m=2n-5 D、m=n2-5二、填空题
-
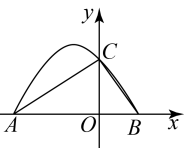
11. 一元二次方程的两个根为 , 则.12. 若是一元二次方程的两个根,则的值是.13. 设a、b是方程的两个不等的根,则的值.14. 已知一元二次方程的两个根为 , 则的值为 .15. 如图,若抛物线与x轴交于A、B两点,与y轴交于点C,若.则的值为.
三、解答题
-
16. 已知关于x的方程的两个实根为 , .且满足 , 试求这个方程的两个实根及k的值.17. 反比例函数y= 的图象上有一点P(m,n),其中坐标是关于t的一元二次方程t2﹣3t+k=0的两根,且P点到原点的距离为 ,求反比例函数的解析式.18. 已知关于x的一元二次方程x2 = 2(1—m)x—m2的两实数根为x1 , x2 ,
(1)求m的取值范围;
(2)设y = x1 + x2 , 当y取得最小值时,求相应m的值,并求出y的最小值。19. 已知关于x的方程x2-2(k-1)x+k2=0有两个实数根x1 , x2 .
⑴求k的取值范围;
⑵若|x1+x2|=x1x2-1,求k的值.四、综合题
-
20. 如图,抛物线:与x轴交于 , 两点,与y轴交于点C.
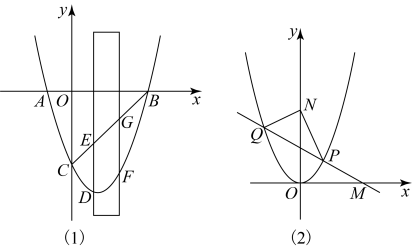 (1)、直接写出抛物线的解析式;(2)、如图(1),有一宽度为1的直尺平行于y轴,在点O,B之间平行移动,直尺两长边被线段和抛物线截得两线段 , .设点D的横坐标为t,且 , 试比较线段与的大小;(3)、如图(2),将抛物线平移得到顶点为原点的抛物线 , M是x轴正半轴上一动点,.经过点M的直线交抛物线于P,Q两点.当点M运动到某一个位置时,存在唯一的一条直线 , 使 , 求点M的坐标.21. 已知、是关于的一元二次方程的两个实数根.(1)、求的取值范围;(2)、是否存在实数根 , 使成立,若存在,求出的值,若不存在,请说明理由.22. 已知关于x的一元二次方程x2+(2m﹣3)x+m2=0有两个实数根x1 , x2.(1)、求实数m的取值范围;(2)、若x1+x2=6﹣x1x2 , 求m的值.23. 在平面直角坐标系中,我们不妨把纵坐标的值与横坐标的值的平方相等的点称为“雅心点”,例如点( , 1),(0,0),( , 2),…都是“雅心点”,显然,这样的“雅心点”有无数个.(1)、求一次函数上的所有“雅心点”的坐标为;(2)、若过点(1,)的直线上恰好只有一个“雅心点”,请求出符合要求的直线解析式;(3)、若二次函数(a是常数,a>0)的图象上存在两个不同的“雅心点”,且“雅心点”的横坐标的值都不大于2,试求实数a的取值范围.
(1)、直接写出抛物线的解析式;(2)、如图(1),有一宽度为1的直尺平行于y轴,在点O,B之间平行移动,直尺两长边被线段和抛物线截得两线段 , .设点D的横坐标为t,且 , 试比较线段与的大小;(3)、如图(2),将抛物线平移得到顶点为原点的抛物线 , M是x轴正半轴上一动点,.经过点M的直线交抛物线于P,Q两点.当点M运动到某一个位置时,存在唯一的一条直线 , 使 , 求点M的坐标.21. 已知、是关于的一元二次方程的两个实数根.(1)、求的取值范围;(2)、是否存在实数根 , 使成立,若存在,求出的值,若不存在,请说明理由.22. 已知关于x的一元二次方程x2+(2m﹣3)x+m2=0有两个实数根x1 , x2.(1)、求实数m的取值范围;(2)、若x1+x2=6﹣x1x2 , 求m的值.23. 在平面直角坐标系中,我们不妨把纵坐标的值与横坐标的值的平方相等的点称为“雅心点”,例如点( , 1),(0,0),( , 2),…都是“雅心点”,显然,这样的“雅心点”有无数个.(1)、求一次函数上的所有“雅心点”的坐标为;(2)、若过点(1,)的直线上恰好只有一个“雅心点”,请求出符合要求的直线解析式;(3)、若二次函数(a是常数,a>0)的图象上存在两个不同的“雅心点”,且“雅心点”的横坐标的值都不大于2,试求实数a的取值范围.