（冀教版）2023-2024学年九年级数学上册24.2 解一元二次方程期中复习

试卷更新日期：2023-07-03 类型：复习试卷

进入出卷网下载

一、选择题

1. 若关于x的一元二次方程 ( k-2)x²-2x+1=0有两个不相等的实数根，且k为非负整数，则符合条件的k的个数为（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
2. 已知一元二次方程 $x^{2} + 4 x - 3 = 0$ ，下列配方正确的是（）

A、 ${(x + 2)}^{2} = 3$ B、 ${(x - 2)}^{2} = 3$ C、 ${(x + 2)}^{2} = 7$ D、 ${(x - 2)}^{2} = 7$

查看试题解析
3. 方程 $x^{2} = 3 x$ 的解为（　　）

A、 $x = 3$ B、 $x = 0$ C、 $x_{1} = 0 ， x_{2} = - 3$ D、 $x_{1} = 0 ， x_{2} = 3$

查看试题解析
4. 关于x的方程 $x^{2} + m x - m^{2} = - 5$ 的一个根是4，那么m的值是（）

A、-3或4 B、 $- 3$ 或7 C、3或4 D、3或7

查看试题解析
5. 若一元二次方程 $a x^{2} - x + 2 = 0$ 有两个不相等的实数根，则实数a的取值范围为（）

A、 $a < \frac{1}{8}$ B、 $a < \frac{1}{8}$ 且 $a \neq 0$ C、 $a \leq \frac{1}{8}$ 且 $a \neq 0$ D、 $a > \frac{1}{8}$

查看试题解析
6. 把方程 $x^{2} - 4 x - 5 = 0$ 化成 ${(x + a)}^{2} = b$ 的形式，则 $a$ 、 $b$ 的值分别是（）

A、2，9 B、2，7 C、-2，9 D、-2，7

查看试题解析
7. 一元二次方程 $x^{2} + 2 x - 1 = 0$ 的根的情况是（）

A、只有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根

查看试题解析
8. 用配方法解一元二次方程 $x^{2} - 6 x + 1 = 0$ 时，下列变形正确的是（）

A、 $(x - 3)^{2} = 1$ B、 $(x - 3)^{2} = 10$ C、 $(x + 3)^{2} = 8$ D、 $(x - 3)^{2} = 8$

查看试题解析
9. 若关于x的一元二次方程 $(k - 2) x^{2} + 2 x - 1 = 0$ 有实数根，则k的取值范围是（）

A、 $k \leq 1$ B、 $k \leq 1$ 且 $k \neq 2$ C、 $k \geq 1$ 且 $k \neq 2$ D、 $k \geq 2$

查看试题解析
10. 若关于x的一元二次方程 $x^{2} - 4 x + m = 0$ 没有实数根，点 $A (x_{1} ， y_{1})$ 、 $B (x_{2} ， y_{2})$ 是反比例函数 $y = \frac{m}{x}$ 的图象上的两个点，若x₁<x₂<0，则y₁、y₂的大小关系为（）

A、y₁>y₂ B、y₁<y₂ C、y₁=y₂ D、不能确定

查看试题解析

二、填空题

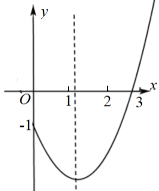
11. 关于x的方程 $x^{2} - 4 x + m = 0$ 有两个相等的实数根，则m的值是.

查看试题解析
12. 方程 $x^{2} = 2 x$ 的解为.

查看试题解析
13. 方程 $x^{2} = 3$ 的根是.

查看试题解析
14. 二次函数 $y = a x^{2} + b x + c$ 图像的一部分如图所示，下列结论：① $a b > 0$ ；② $a - b + c < 0$ ；③ $a x^{2} + b x + c + 1 = 0$ 有两个相等的实数根；④ $- 4 a < b < - 2 a$ .其中正确的为（只填序号）.

查看试题解析
15. 已知关于x的一元二次方程 $(x - 2) (x - 3) = m$ 有实根x₁ ， x₂ ，且x₁＜x₂ ，现有下列说法： ①当m=0时，x₁=2，x₂=3；②当m>0时，2＜x₁＜x₂＜3；③ $m > - \frac{1}{4}$ ；④二次函数 $y = (x - x_{1}) (x - x_{2}) - m$ 的图象与x轴的交点坐标为（2，0）和（3，0）. 其中正确的有.

查看试题解析

三、解答题

16. 请你先认真阅读下列材料，再参照例子解答问题：
已知 $(x + y - 3) (x + y + 4) = - 10$ ，求 $x + y$ 的值；
解：设 $x + y = t$ ，则原方程可变形为 $(t - 3) (t + 4) = - 10$ .即 $t^{2} + t - 2 = 0$
∴ $(t + 2) (t - 1) = 0$ 得 $t_{1} = - 2$ ， $t_{2} = 1$
∴ $x + y = - 2$ 或 $x + y = 1$
已知 $(x^{2} + y^{2} - 2) (x^{2} + y^{2} - 3) = 12$ ，求 $x^{2} + y^{2}$ 的值.

查看试题解析
17. 已知矩形ABCD两邻边AB、BC的长是关于x的方程 $x^{2} - 2 m x + 4 m - 4 = 0$ 的两个实数根.当m为何值时，矩形ABCD的两邻边AB、BC的长相等.

查看试题解析
18. 已知 $x$ 为方程 $x ² + x - 6 = 0$ 的根，化简 $(x - 1) \div (\frac{2}{x - 1} - 1)$ 并求值.

查看试题解析
19. 阅读下面的例题，
范例：解方程 $x^{2} - | x | - 2 = 0$ ，

解：（1）当 $x \geq 0$ 时，原方程化为 $x^{2} - x - 2 = 0$ ，解得： $x_{1} = 2$ ， $x_{2} = - 1$ （不合题意，舍去）.
（2）当x＜0时，原方程化为 $x^{2} + x - 2 = 0$ ，解得： $x_{1} = - 2$ ， $x_{2} = 1$ （不合题意，舍去）.

∴原方程的根是 $x_{1} = 2$ ， $x_{2} = - 2$ ，请参照例题解方程 $x^{2} - | x - 1 | - 1 = 0$

查看试题解析

四、综合题

20. 已知关于x的一元二次方程 $x^{2} + 4 x + k = 0$ 有两个实数根.

(1)、求k的取值范围；

(2)、取一个合适的k的值，使得方程的解为负整数并求出此时方程的解.

查看试题解析
21. 已知：平行四边形 $A B C D$ 的两边 $A B$ ， $A D$ 的长是关于x的方程 $x^{2} - m x + m - 1 = 0$ 的两个实数根.

(1)、m为何值时，四边形 $A B C D$ 是菱形？

(2)、若 $A B$ 的长为3，求 $▱ A B C D$ 的周长.

查看试题解析
22. 已知关于x的方程 $x^{2} - 3 a x - 3 a - 6 = 0$ ，

(1)、求证：方程恒有两不等实根；

(2)、若x₁ ， x₂是该方程的两个实数根，且 $(x_{1} - 1) (x_{2} - 1) = 1$ ，求a的值.

查看试题解析
23. 定义：已知 $x_{1} ， x_{2}$ 是关于x的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的两个实数根，若 $x_{1} < x_{2} < 0$ ，且 $3 < \frac{x_{1}}{x_{2}} < 4$ ，则称这个方程为“限根方程”.如：一元二次方程 $x^{2} + 13 x + 30 = 0$ 的两根为 $x_{1} = - 10 ， x_{2} = - 3$ ，因 $- 10 < - 3 < 0$ ， $3 < \frac{- 10}{- 3} < 4$ ，所以一元二次方程 $x^{2} + 13 x + 30 = 0$ 为“限根方程”.
请阅读以上材料，回答下列问题：

(1)、判断一元二次方程 $x^{2} + 9 x + 14 = 0$ 是否为“限根方程”，并说明理由；

(2)、若关于x的一元二次方程 $2 x^{2} + (k + 7) x + k^{2} + 3 = 0$ 是“限根方程”，且两根 $x_{1} 、 x_{2}$ 满足 $x_{1} + x_{2} + x_{1} x_{2} = - 1$ ，求k的值；

(3)、若关于x的一元二次方程 $x^{2} + (1 - m) x - m = 0$ 是“限根方程”，求m的取值范围.

查看试题解析

（冀教版）2023-2024学年九年级数学上册24.2 解一元二次方程 期中复习

一、选择题

二、填空题

三、解答题

四、综合题

（冀教版）2023-2024学年九年级数学上册24.2 解一元二次方程期中复习