（冀教版）2023-2024学年九年级数学上册23.3 方差期中复习

试卷更新日期：2023-07-03 类型：复习试卷

进入出卷网下载

一、选择题

1. 已知一组数据a、b、c、d的平均数是3，在这组数据后再添加数据3得到一组新数据a、b、c、d、3，则新数据与原数据相比，方差将（）

A、不变 B、变大 C、变小 D、不能确定

查看试题解析
2. 甲、乙、丙、丁四人进行射击测试，每人测试10次，平均成绩均为9.2环，方差如表所示．则在这四个选手中，成绩最稳定的是（）
选手
甲
乙
丙
丁
方差
$0.56$
$0.60$
$0.50$
$0.45$

A、甲 B、乙 C、丙 D、丁

查看试题解析
3. 某校举行体操比赛，甲、乙两个班各选18名学生参加比赛，两个班参赛学生的平均身高都是1.72米，其方差分别是 $S_{甲}^{2} = 3.24$ ， $S_{乙}^{2} = 1.63$ ，则参赛学生身高比较整齐的班级是（）

A、甲班 B、乙班 C、同样整齐 D、无法确定

查看试题解析
4. 为了向建党一百周年献礼，我市中小学生开展了红色经典故事演讲比赛 $.$ 某参赛小组 $6$ 名同学的成绩 $($ 单位：分 $)$ 分别为：85，82，86，82，83，92关于这组数据，下列说法错误的是（）

A、众数是82 B、中位数是84 C、方差是84 D、平均数是85

查看试题解析
5. 甲、乙、丙、丁四人进行射击测试，他们在相同条件下各射击10次，成绩（单位：环）统计如表：

甲
乙
丙
丁
平均数
9.6
9.5
9.5
9.6
方差
0.28
0.27
0.25
0.25
若从这四人中，选出一位成绩较好且状态稳定的选手参加比赛，那么应选（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 甲，乙，丙，丁四人进行射击测试，每人10次射击的平均成绩恰好都是9.2环，方差分别是 $s_{甲}^{2} = 0.12$ ， $s_{乙}^{2} = 0.59$ ， $s_{丙}^{2} = 0.33$ ， $s_{丁}^{2} = 0.46$ ，在本次射击测试中，这四个人成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 如图是根据打绳巷米面店今年6月1日至5日每天的用水量（单位：吨）绘制成的折线统计图．下列结论正确的是（）

A、平均数是6 B、中位数是7 C、众数是7 D、方差是7

查看试题解析
8. 甲乙两人5次射击命中的次数如下：
甲
7
9
8
6
10
乙
7
8
9
8
8
则这两人次射击命中的环数的平均数都为8，则甲的方差与乙的方差的大小关系为（）

A、甲的方差大 B、乙的方差大 C、两个方差相等 D、无法判断

查看试题解析
9. 我校准备挑选一名跳高运动员参加全市中学生运动会，对跳高运动队的甲、乙两名运动员进行了8次选拔比赛.他们的成绩（单位：m）如下：
甲
1.70
1.65
1.68
1.69
1.72
1.73
1.68
1.67
乙
1.60
1.73
1.72
1.61
1.62
1.71
1.70
1.75
借助计算器判断运动员的成绩更为稳定的是（）

A、甲 B、乙 C、一样稳定 D、无法判断

查看试题解析
10. 小明根据演讲比赛中9位评委所给的分数制作了如下表格：

平均数

中位数

众数

方差

8.0

8.2

8.3

0.2

如果去掉一个最高分和一个最低分，那么表格中数据一定不发生变化的是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析

二、填空题

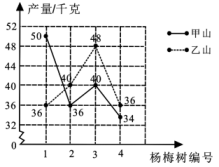
11. 如果一组数据3，5，x，6，8的众数为3，那么这组数据的方差为 .

查看试题解析
12. 在一次跳远训练中，甲、乙两人每人5次跳远的平均成绩都是 $7.68$ 米，方差分别是 $s_{甲}^{2} = 0.92$ （米 $^{2}$ ）， $s_{乙}^{2} = 1.12$ （米 $^{2}$ ），则在这次跳远训练中成绩比较稳定的是.

查看试题解析
13. 王大伯前几年承包了甲、乙两片荒山，各栽种了100棵杨梅树，成活98%，现已挂果，经济效益初步显现，为了分析收成情况，他分别从两山上随意各采摘了四棵杨梅树上的杨梅，每棵的产量如图所示，由统计图提供的信息可知，杨梅产量较稳定的是.

查看试题解析
14. 小聪同学在计算一组数据1、3、4、5、x的方差时，写出的计算过程是： $S^{2} = \frac{1}{5} [(1 - 4)^{2} + (3 - 4)^{2} + (4 - 4)^{2} + (5 - 4)^{2} + (x - 4)^{2}] = 4$ ，如果他的计算是正确的，你认为这组数据中的x为．

查看试题解析
15. 农科院计划为某地选择合适的水果玉米种子，通过实验，甲、乙、丙、丁四种水果玉米种子每亩平均产量都是1500kg，方差分别为 $S_{甲}^{2} = 0.02$ ， $S_{乙}^{2} = 0.02$ ， $S_{丙}^{2} = 0.03$ ， $S_{丁}^{2} = 0.01$ ，则这四种水果玉米种子产量最稳定的是．（填“甲”“乙”“丙”“丁”）

查看试题解析

三、解答题

16. 如图，是甲、乙两名射击运动员一次训练中10次射击环数折线统计图，请判断甲、乙两名射击运动员中谁的成绩的方差小，并计算其方差.

查看试题解析
17. 某学校为选拔数学能力突出的学生参加中学生数学竞赛，组织了多次测试，其中甲乙两位同学成绩较为优秀，他们在六次赛前测试中的成绩（单位：分）如下表所示．

甲

80

75

90

64

88

95

乙

84

80

88

76

79

85

如果根据这六次成绩选拔其中一人参加比赛，你认为哪一位比较合适？为什么？

查看试题解析
18. 学校运动会开设了“抢收抢种”项目，八(5)班甲，两个队伍都想代表班级参赛，为了选择一个比较好的队伍，八(5)班的班委组织了一次选拔赛，甲，乙两队各5人的比赛成绩如下表(单位：分)：

甲队

7

8

10

7

9

乙对

7

8

7

9

9

经计算，甲队比赛成绩的平均数为8分，方差为1.2，请计算乙队比赛成绩的方差，并根据计算结果，帮助班委选择一个成绩比较稳定的队伍代表班级参赛.

查看试题解析

19. 为庆祝中国共产党建党100周年，某校举行了“红色华诞，党旗飘扬”党史知识竞赛.为了解竞赛成绩，抽样调查了七，八年级部分学生的分数，过程如下：

（ 1 ）收集数据从该校七.八年级学生中各随机抽取20名学生的分数，其中八年级的分数如下：

81 83 84 85 86 87 87 88 89 90

92 92 93 95 95 95 99 99 100 100

（ 2 ）整理、描述数据按如下分段整理描述样本数据：

分数 $x$

人数

年级

$80 \leq x < 85$

$85 \leq x < 90$

$90 \leq x < 95$

$95 \leq x \leq 100$

七年级

八年级

$a$

（ 3 ）分析数据两组样本数据的平均数、中位数、众数、方差如下表所示：

年级	平均数	中位数	众数	方差
七年级	91	89	97	40.9
八年级	91	$b$	$c$	33.2

根据以上提供的信息，解答下列问题：

①填空： $a =$ ， $b =$ ， $c =$ ；

②样本数据中，七年级甲同学和八年级乙同学的分数都为90分，同学的分数在本年级抽取的分数中从高到低排序更靠前（填“甲”或“乙”）：

③从样本数据分析来看，分数较整齐的是年级（填“七”或“八”）；

④如果七年级共有400人参赛，则该年级约有人的分数不低于95分.

查看试题解析

四、综合题

20. 公司生产 $A$ 、 $B$ 两种型号的扫地机器人，为了解它们的扫地质量，工作人员从某月生产的 $A$ 、 $B$ 型扫地机器人中各随机抽取10台，在完全相同条件下试验，记录下它们的除尘量的数据（单位： $g$ ），并进行整理、描述和分析（除尘量用 $x$ 表示，共分为三个等级：合格 $80 \leq x < 85$ ，良好 $85 \leq x < 95$ ，优秀 $x \geq 95$ ），下面给出了部分信息：
10台 $A$ 型扫地机器人的除尘量：83，84，84，88，89，89，95，95，95，98.
10台 $B$ 型扫地机器人中“良好”等级包含的所有数据为：85，90，90，90，94
抽取的 $A$ 、 $B$ 型扫地机器人除尘量统计表
型号
平均数
中位数
众数
方差
“优秀”等级所占百分比
$A$
90
89
$a$
26.6
$40 %$
$B$
90
$b$
90
30
$30 %$
根据以上信息，解答下列问题：

(1)、填空： $a =$ ， $b =$ ， $m =$ ；

(2)、这个月公司可生产 $B$ 型扫地机器人共3000台，估计该月 $B$ 型扫地机器人“优秀”等级的台数；

(3)、根据以上数据，你认为该公司生产的哪种型号的扫地机器人扫地质量更好？请说明理由（写出一条理由即可）.

查看试题解析
21. 甲、乙两名队员参加射击选拔赛，射击成绩见下列统计图：
根据以上信息，整理分析数据如下：
队员
平均数（环）
中位数（环）
众数（环）
方差（ $环^{2}$ ）
甲
7.9
$b$
$c$
4.09
乙
$a$
7
7
$d$

(1)、直接写出表格中 $a$ ， $b$ ， $c$ 的值；

(2)、求出 $d$ 的值；

(3)、若从甲、乙两名队员中选派其中一名队员参赛，你认为应选哪名队员？请结合表中的四个统计量，作出简要分析．

查看试题解析

22. 某中学组织七、人年级全体学生开展了“禁毒知识”网上竞赛活动，为了解竞赛情况，从七、八年级中各随机抽取了10名同学的成绩(满分为100分).

收集数据：

七年级	90	95	95	80	90	80	85	100	85	100
八年级	85	85	95	80	95	90	90	90	100	90

整理数据：

	80	85	90	95	100
七年级	2	2	2	2	2
八年级	1	2	4	2	1

分析数据：

年级	平均数	中位数	众数	方差
七年级	90	____	90	50
八年级	____	90	90	30

根据以上信息回答下列问题：

(1)、请完成表格中的空格.

(2)、通过数据分析，你认为哪个年级学生的成绩比较好?请说明理由.

(3)、若该校七、人年级共有1600人，本次竞赛成绩不低于95分的为“优秀”，试估计这两个年级共有多少名学生达到“优秀”.

查看试题解析

23. 为庆祝中国共产主义青年团成立100周年，学校团委在八、九年级各抽取50名团员开展团知识竞赛，为便于统计成绩，制定了取整数的计分方式，满分10分．竞赛成绩如图所示：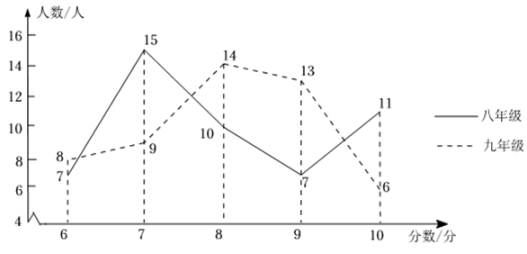

(1)、你能用成绩的平均数判断哪个年级的成绩比较好吗？通过计算说明；

(2)、请根据图表中的信息，回答下列问题．

	众数	中位数	方差
八年级竞赛成绩	7	8	1.88
九年级竞赛成绩	$a$	8	$b$

①表中的 $a =$ ▲ ， $b =$ ▲ ；

②现要给成绩突出的年级颁奖，如果分别从众数和方差两个角度来分析，你认为应该给哪个年级颁奖？

(3)、若规定成绩10分获一等奖，9分获二等奖，8分获三等奖，则哪个年级的获奖率高？

查看试题解析

甲	1.70	1.65	1.68	1.69	1.72	1.73	1.68	1.67
乙	1.60	1.73	1.72	1.61	1.62	1.71	1.70	1.75

型号	平均数	中位数	众数	方差	“优秀”等级所占百分比
$A$	90	89	$a$	26.6	$40 %$
$B$	90	$b$	90	30	$30 %$

队员	平均数（环）	中位数（环）	众数（环）	方差（ $环^{2}$ ）
甲	7.9	$b$	$c$	4.09
乙	$a$	7	7	$d$

选手	甲	乙	丙	丁
方差	$0.56$	$0.60$	$0.50$	$0.45$

	甲	乙	丙	丁
平均数	9.6	9.5	9.5	9.6
方差	0.28	0.27	0.25	0.25

平均数	中位数	众数	方差
8.0	8.2	8.3	0.2

甲队	7	8	10	7	9
乙对	7	8	7	9	9

（冀教版）2023-2024学年九年级数学上册23.3 方差 期中复习

一、选择题

二、填空题

三、解答题

四、综合题

（冀教版）2023-2024学年九年级数学上册23.3 方差期中复习