(冀教版)2023-2024学年九年级数学上册23.2 中位数与众数 期中复习
试卷更新日期:2023-07-03 类型:复习试卷
一、选择题
-
1. 下列说法正确的是( )A、甲、乙两人跳远成绩的方差分别为s甲2=3,s乙2=4,说明乙的跳远成绩比甲稳定 B、了解某市市民知晓“礼让行人”交通新规的情况,适合全面调查 C、一组数据2,2,3,4的众数是2,中位数是2.5 D、可能性是1%的事件在一次试验中一定不会发生2. 已知、、、、是按从小到大顺序排列的5个连续整数,若将这组数据变为、、、、 , 则这组新数据与原来相比( )A、平均数变大 B、中位数变小 C、极差变大 D、方差变小3. 据了解,某定点医院收治的6名“新型冠状肺炎”患者的新冠病毒潜伏期分别为2天,3天,3天,3天,4天,5天,则这6名患者新冠病毒潜伏期的众数为( )A、2天 B、3天 C、4天 D、5天4. 一组数据为7,9,9,11,若添加一个数据9,则发生变化的统计量是( )A、方差 B、众数 C、中位数 D、平均数5. 小红在“养成阅读习惯,快乐阅读,健康成长”读书大赛活动中,随机调查了本校初二年级20名同学,在近5个月内每人阅读课外书的数量,数据如下表所示:
人数
3
4
8
5
课外书数量(本)
12
13
15
18
则阅读课外书数量的中位数和众数分别是( )
A、13,15 B、14,15 C、13,18 D、15,156. 为了从甲、乙两名同学中选出一名同学代表班级参加学校的投篮比赛,对甲、乙两人进行了5次投篮试投比赛,试投每人每次投球10个,两人5次试投的成绩统计图如图所示.以下说法错误的是( ) A、甲同学5次试投进球个数的众数是8 B、甲、乙两名同学投篮成绩甲较稳定 C、甲、乙同学5次试投进球个数的平均数相同 D、乙同学5次试投进球个数的中位数是87. 在射击训练中,某队员的10次射击成绩如图,则这10次成绩的中位数和众数分别是( )
A、甲同学5次试投进球个数的众数是8 B、甲、乙两名同学投篮成绩甲较稳定 C、甲、乙同学5次试投进球个数的平均数相同 D、乙同学5次试投进球个数的中位数是87. 在射击训练中,某队员的10次射击成绩如图,则这10次成绩的中位数和众数分别是( )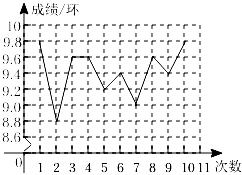 A、9.3,9.6 B、9.5,9.4 C、9.5,9.6 D、9.6,9.88. 一组数据1,2,2,3下列说法正确的是( )A、众数是3 B、中位数是2 C、极差是3 D、平均数是39. 某中学篮球队13名队员的年龄情况如下:
A、9.3,9.6 B、9.5,9.4 C、9.5,9.6 D、9.6,9.88. 一组数据1,2,2,3下列说法正确的是( )A、众数是3 B、中位数是2 C、极差是3 D、平均数是39. 某中学篮球队13名队员的年龄情况如下:年龄单位:岁
15
16
17
18
人数
3
4
5
1
则这个队队员年龄中的中位数和众数分别是( )
A、15.5和5 B、16和17 C、16.5和16 D、17和510. 一组数据:-1,1,3,4,a,若它们的平均数为2,则这组数据的众数为( )A、1 B、2 C、3 D、4二、填空题
-
11. 已知一组数据为1,10,6,4,7,4,则这组数据的众数为 .12. 一组数据18,22,15,13,x,7,它的中位数是16,则x的值是 .13. 小燕的父亲近六个月的手机话费(单位:元)如下:81,75,70,64,98,92.这组数据的中位数是 .14. 从2022年起长沙市学校体育中考增加素质类选测项目:立定跳远和1分钟跳绳.小熙选择了1分钟跳绳项目,她10次跳绳训练的成绩为140,155,142,155,166,167,166,170,180,176,这组数据的中位数是.15. 已知一组数据由五个正整数组成,中位数是2,众数是2,且最大的数小于3,则这组数据之和的最小值是 .
三、解答题
-
16. 某社区为了增强居民节约用水的意识,随机调查了部分家庭一年的月均用水量(单位:t).根据调查结果,绘制出如下的统计图①和图②.

请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的家庭个数为 ,图①中m的值为 ;
(Ⅱ)求统计的这组月均用水量数据的平均数、众数和中位数.
17. 某学校为了了解本校1200名学生的课外阅读的情况,现从各年级随机抽取了部分学生,对他们一周的课外阅读时间进行了调查,井绘制出如下的统计图①和图②,根据相关信息,解答下列问题: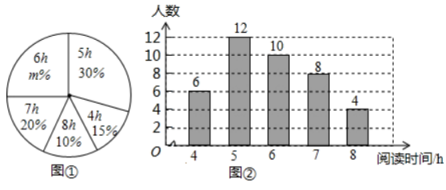
(Ⅰ)本次接受随机抽样调查的学生人数为 , 图①中的值为 ;
(Ⅱ)求本次调查获取的样本数据的众数、中位数和平均数;
(Ⅲ)根据样本数据,估计该校一周的课外阅读时间大于的学生人数.
18. 北京人大附中小强同学学完“数据分析”的相关知识后后,就回家帮助母亲预算家庭一年煤气开支,他连续7个月估计了每个月的家庭煤气使用数据,并记录如下表:日期
11月1日
12月1日
1月1日
2月1日
3月1日
4月1日
5月1日
使用量(方)
9.41
9.59
9.74
9.93
10.13
10.13
11.07
①写出这7个月每月用煤气数的众数、中位数、平均数.
②若每方煤气需要支出2.2元,估计小强家一年的煤气费大约为多少元?
19. 在一次“爱心助学”捐款活动中,全校同学人人拿出自己的零花钱,踊跃捐款,学生捐款额有5元、10元、15元、20元四种情况.李老师在全校范围内随机抽取部分学生,对捐款金额进行了统计,根据统计结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题: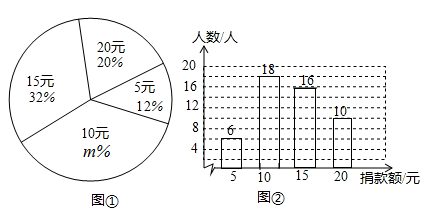 (1)、本次抽取的学生人数为 ,图①中 的值为;(2)、求统计的这组学生捐款数据的平均数、众数和中位数;(3)、根据统计的学生捐款的样本数据,若该校共有800名初中学生,估计该校学生共捐款的钱数.
(1)、本次抽取的学生人数为 ,图①中 的值为;(2)、求统计的这组学生捐款数据的平均数、众数和中位数;(3)、根据统计的学生捐款的样本数据,若该校共有800名初中学生,估计该校学生共捐款的钱数.四、综合题
-
20. 某校举行“中国共产党十九大”知识问答竞赛.每班选20名同学参加比赛.根据答对的题目数量得分,等级分为5分,4分,3分,2分.学校将八年级甲班和乙班的成绩整理并绘制成如下的统计图.
甲班知识问答成绩统计图 乙班知识问答成绩统计图

甲、乙两班成绩统计表
班级
平均数(分)
中位数(分)
众数(分)
甲班
a
4
4
乙班
3.6
3.5
b
(1)、请把甲班知识问答成绩统计图补充完整.(2)、通过统计得到上表,请求出表中数据a,b的值.(3)、根据(2)的结果,你认为甲,乙两班哪个班级成绩更好?写出你的理由.21. 为了进一步了解某校初中学生的体质健康状况,对九年级的部分学生进行了体质抽测.同时统计了每个人的得分.体质抽测的成绩分为四个等级:优秀、良好、合格 , 不合格根据调查结果绘制了下列两福不完整的统计图,请你根据统计图提供的信息回答以下问题: (1)、补全上面的扇形统计图和条形统计图;(2)、被测试的部分九年级学生的体质测试成绩的中位数落在等级;(3)、若该校九年级有1200名学生,估计该校九年级体质为“不合格”的学生约有多少人?22. 为了从甲、乙两位同学中选拔一人参加知识竞赛,举行了6次选拔赛,根据两位同学6次选拔赛的成绩,分别绘制了如图统计图.
(1)、补全上面的扇形统计图和条形统计图;(2)、被测试的部分九年级学生的体质测试成绩的中位数落在等级;(3)、若该校九年级有1200名学生,估计该校九年级体质为“不合格”的学生约有多少人?22. 为了从甲、乙两位同学中选拔一人参加知识竞赛,举行了6次选拔赛,根据两位同学6次选拔赛的成绩,分别绘制了如图统计图.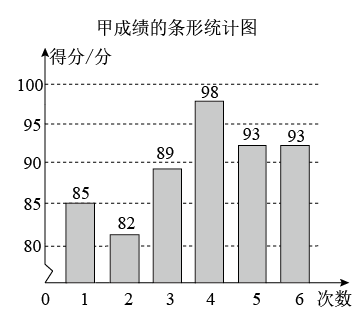
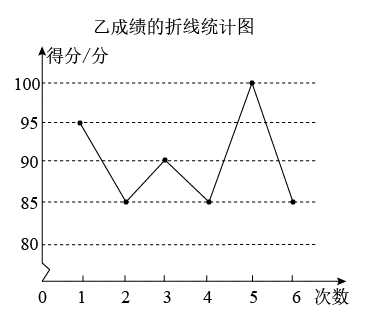 (1)、填写下列表格
(1)、填写下列表格平均数/分
中位数/分
众数/分
甲
90
①
93
乙
②
87.5
③
(2)、已求得甲同学6次成绩的方差为(分2),求出乙同学6次成绩的方差;(3)、你认为选择哪一位同学参加知识竞赛比较好?请说明理由.23. 2022年3月25日,教育部印发《义务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来.某校为了解该校学生一周的课外劳动情况,随机抽取部分学生调查了他们一周的课外劳动时间,将数据进行整理并制成如下统计图.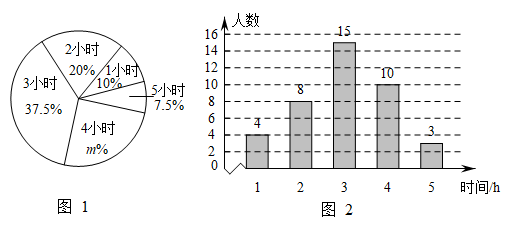
请根据图中提供的信息,解答下面的问题:
(1)、求图1中的m= , 本次调查数据的中位数是h,本次调查数据的众数是h;(2)、该校此次抽查的这些学生一周平均的课外劳动时间是多少?(3)、若该校共有2000名学生,请根据统计数据,估计该校学生一周的课外劳动时间不小于的人数.