（冀教版）2023-2024学年九年级数学上册23.1 平均数与加权平均数期中复习

试卷更新日期：2023-07-03 类型：复习试卷

进入出卷网下载

一、选择题

1. 已知 $x_{1}$ 、 $x_{2}$ 、 $x_{3}$ 、 $x_{4}$ 、 $x_{5}$ 是按从小到大顺序排列的5个连续整数，若将这组数据变为 $x_{1} + 1$ 、 $x_{2} + 1$ 、 $x_{3}$ 、 $x_{4} - 1$ 、 $x_{5} - 1$ ，则这组新数据与原来相比（）

A、平均数变大 B、中位数变小 C、极差变大 D、方差变小

查看试题解析
2. 下表记录了甲、乙、丙、丁四名同学参加某区“十九届六中全会”为主题的演讲比赛的相关数据：根据表中数据，从平均成绩优秀且成绩稳定的角度，选择甲同学参加市级比赛，则可以判断a、b的值可能是（）

甲
乙
丙
丁
平均数（分）
$a$
80
90
80
方差
$b$
2.2
5.4
2.4

A、95，6 B、95，2 C、85，2 D、85，6

查看试题解析
3. 一组数据为7，9，9，11，若添加一个数据9，则发生变化的统计量是（）

A、方差 B、众数 C、中位数 D、平均数

查看试题解析
4. 小娅在对数据 $26 ， 30 ， 30 ， 43 ， 5 * ， 57$ 进行统计分析时，发现其中一个两位数的个位数字被墨水涂污看不到了，则计算结果不受影响的统计量是（）

A、平均数 B、中位数 C、方差 D、众数

查看试题解析
5. 甲、乙、丙、丁四人10次随堂测验的成绩如图所示，从图中可以看出这10次测验平均成绩较高且较稳定的是（）

A、 B、 C、 D、

查看试题解析
6. 希望中学规定学生的学期体育成绩满分为 $100$ ，其中体育课外活动占20%，期中考试成绩占30%，期末考试成绩占50%若小强的三项成绩 $($ 百分制 $)$ 依次是95，90，91则小强这学期的体育成绩是（）

A、92 B、91.5 C、91 D、90

查看试题解析
7. 在计算器上，小明将按键顺序 $($ $c o s$ $6$ $0$ $)$ $y^{x}$ $3$ $=$ 的显示结果记为a， $M O D E$ $2$ $3$ $D A T E$ $4$ $D A T E$ $D A T E$ $5$ $D A T E$ $\bar{x}$ $=$ 的显示结果记为b，则a与b的乘积为（）

A、 $\frac{1}{2}$ B、 $\frac{27}{2}$ C、 $\frac{9}{8}$ D、6

查看试题解析
8. 用计算器计算13.49，13.55，14.07，13.51，13.84，13.98的平均数为（）

A、13.53 B、13.61 C、13.74 D、14.00

查看试题解析
9. 一组数据x、0、1、－2、3的平均数是1，则x的值是（）

A、3 B、1 C、2.5 D、0

查看试题解析
10. 某校进行广播操比赛，如图是20位评委给某班的评分情况统计图，则该班平均得分（　　）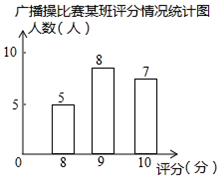

A、9 B、6.67 C、9.1 D、6.74

查看试题解析

二、填空题

11. 某校体育期末考核“仰卧起坐”和“ $800$ 米”两项，并按 $3 ： 7$ 的比例算出期末成绩.已知小林这两项的考试成绩分别为 $80$ 分、 $90$ 分，则小林的体育期末成绩为分.

查看试题解析
12. 某校拟招聘一批优秀教师，其中某位教师笔试、试讲、面试三轮测试得分分别为95分、85分、90分，综合成绩按笔试、试讲、面试的占比为2：2：1，则该名教师的综合成绩为.

查看试题解析
13. 已知4个正数a₁ ， a₂ ， a₃ ， a₄的平均数是a，且a₁＞a₂＞a₃＞a₄ ，则数据a₁ ， a₂ ， 0，a₃ ， a₄的平均数和中位数分别是，．

查看试题解析
14. 我区“引进人才”招聘考试分笔试和面试.其中笔试按60%、面试按40%计算加权平均数作为总成绩.吴老师笔试成绩为95分，面试成绩为85分，那么吴老师的总成绩为分.

查看试题解析
15. 某校举行校园十佳歌手大赛，小张同学的初赛成绩为80分，复赛成绩为90分.若总成绩按初赛成绩占 $40 %$ ，复赛成绩占 $60 %$ 来计算，则小张同学的总成绩为分.

查看试题解析

三、解答题

16. 某公司招聘一名部门经理，对A、B、C三位候选人进行了三项测试，成绩如下（单位：分）：

候选人	语言表达	微机操作	商品知识
A	60	80	70
B	50	70	80
C	60	80	65

如果语言表达、微机操作和商品知识的成绩按3∶3∶4计算，那么谁将会被录取？

查看试题解析

17. 一个可以自由转动的转盘，其盘面分为 $3$ 等份，分别标上数字 $3 ， 4 ， 5$ .小颖准备转动转盘 $5$ 次，现已转动 $3$ 次，每一次停止后，小颖将指针所指数字记录如下：

次数

1

2

3

4

5

数字

4

3

3

小颖继续自由转动转盘2次，判断是否可能发生“这5次指针所指数字的平均数不小于3.6且不大于3.8”的结果？若有可能，计算发生此结果的概率，并写出计算过程；若不可能，请说明理由．(指针指向盘面等分线时为无效转次．)

查看试题解析
18. 我校为了纪念“一二•九”举办了八年级红歌合唱比赛，为了保证这次比赛的公正性，规定：参赛班级的基本素养、精神面貌、服装三项打分分别按5：3：2的比例计入总评成绩．二班、三班、五班的基本素养、精神面貌、服装的打分如下表，计算哪个班是第一名？
基本素养
精神面貌
服装
二班
90
96
93
三班
90
90
96
五班
96
94
90

查看试题解析
19. 为了考察甲、乙两种成熟期小麦的株高长势情况，现从中随机抽取6株，并测得它们的株高（单位：cm）如下表所示：

甲

63

66

63

61

64

61

乙

63

65

60

63

64

63

（Ⅰ）请分别计算表内两组数据的方差，并借此比较哪种小麦的株高长势比较整齐？

（Ⅱ）现将进行两种小麦优良品种杂交实验，需从表内的甲、乙两种小麦中，各随机抽取一株进行配对，以预估整体配对情况，请你用列表法或画树状图的方法，求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.

查看试题解析

四、综合题

20. 省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：

第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8

(1)、根据表格中的数据，计算出甲的平均成绩是环，乙的平均成绩是环；

(2)、分别计算甲、乙六次测试成绩的方差；你认为推荐谁参加全国比赛更合适，请说明理由.

查看试题解析
21. 某节能灯厂出售一批额定功率为 $30 W$ 的节能灯，每盒装有100个节能灯，由于包装工人的疏忽，在包装时混进了额定功率 $15 W$ 的节能灯.某批发商从工厂购进了50盒 $30 W$ 的节能灯，每盒中混入 $15 W$ 灯数如表：
每盒中混入 $15 W$ 灯数（个）
0
1
2
3
4
盒数
14
25
9
1
1

(1)、平均每盒混入几个 $15 W$ 灯？

(2)、若一盒混入 $15 W$ 节能灯的数量大于 $2 %$ ，工厂需给批发商赔偿.从这50盒中任意抽取一盒，记事件A为：该盒需要给批发商赔偿.求事件A的概率.

查看试题解析

22. 教育部规定中小学劳动教育考核纳入学生综合素质档案，以促进学生劳动素养的提升．为了了解本校学生“一周内做家务劳动所用的时间”（简称“劳动时间”）的情况，某校随机调查了

100

名学生的“劳动时间”，并进行统计，绘制了如下统计表：

组别	“劳动时间”t/分钟	频数	组内学生的平均“劳动时间”/分钟
A	$t < 60$	$8$	$50$
B	$60 \leq t \leq 90$	$16$	$75$
C	$90 \leq t \leq 120$	$40$	$100$
D	$t \geq 120$	$a$	$150$
总计		$100$

根据上述信息，解答下列问题：

(1)、表格中

a =

，这

100

名学生的“劳动时间”的中位数落在组（填“A”“B”“C”“D”）；

(2)、求这

100

名学生的平均“劳动时间”；

(3)、若该校有

1200

名学生，请估计在该校学生中，“劳动时间”不少于

60

分钟的人数．