（华师大版）七年级上学期数学微专题复习——近似数

试卷更新日期：2023-07-03 类型：复习试卷

进入出卷网下载

一、选择题

1. 祖冲之是我国古代杰出的数学家，他首次将圆周率 $π$ 精算到小数第七位，即 $3.1415926 < π < 3.1415927$ ，则精确到百分位时 $π$ 的近似值是（）

A、 $3.1$ B、 $3.14$ C、 $3.141$ D、 $3.142$

查看试题解析
2. 用四舍五入法对5.423取近似值，并精确到0.1后的结果是（）

A、5.4 B、5.5 C、5.42 D、5.43

查看试题解析
3. 用四舍五入法对下列各数取近似值，其中错误的是（）.

A、 $304.25 \approx 304$ （精确到个位） B、 $1.804 \approx 1.8$ （精确到十分位） C、 $2.602 \approx 2.6$ （精确到0.01） D、 $1205 \approx 1.2 \times 1 0^{3}$ （精确到百位）

查看试题解析
4. 下列判断中，正确的是（）

A、-2是负数，但不是有理数 B、3a²bc与-bca²是同类项 C、8万与80000的精确度相同 D、多项式-x³+5x²y-3xy²+y³是按y的降幂排列

查看试题解析
5. 已知a是一个三位小数，用四舍五入法得到a的近似数是3.80，则a的取值范围是（）

A、 $3.750 < a < 3.854$ B、 $3.750 \leq a < 3.854$ C、 $3.795 < a < 3.805$ D、 $3.795 \leq a < 3.805$

查看试题解析
6. 用四舍五入法，把2.345精确到百分位的近似数是（）

A、2.3 B、2.34 C、2.35 D、2.30

查看试题解析
7. 下列说法正确的是（）

A、 $x^{2} + 2 x y + y^{2}$ 是二次三项式 B、 $3^{2} x^{3} y$ 的次数是6 C、 $2.46$ 万精确到百分位 D、 $- \frac{6 π x^{2} y^{3}}{5}$ 的系数是 $- \frac{6}{5}$

查看试题解析
8. 下列结论：
①-2⁴的底数是-2；

②若有理数a，b互为相反数，那么a+b=0；

③把1.804精确到0.01约等于1.80；

④化简（5a-3b）-3（a²-2b）的结果是-3a²+5a+3b；

⑤式子|a+2|+6的最大值是6。

其中正确的个数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
9. 近似数13.7万精确到（　　）

A、十分位 B、百位 C、千位 D、千分位

查看试题解析
10. 国家疾控中心网站显示：截至2022年9月28日，全国累计报告接种新冠疫苗34亿3663万剂次，覆盖人数13亿323.2万元，其中数据3663万用科学记数法（精确到百万位）表示为（）

A、 $3.663 \times 1 0^{7}$ B、 $0.36 \times 1 0^{8}$ C、 $3.7 \times 1 0^{7}$ D、 $3.7 \times 1 0^{8}$

查看试题解析

二、填空题

11. $79.58 \approx$ .（精确到十分位）

查看试题解析
12. 用四舍五入法，对 $0.2356$ 精确到百分位得到的近似数为．

查看试题解析
13. 由四舍五入得到的近似数 $8.31 \times 1 0^{5}$ 精确到位．

查看试题解析
14. 下列说法：①整数和分数统称为有理数；② $| a | - a \leq 0$ ；③倒数等于它本身的数只有 $\pm 1$ ；④ $- \frac{2^{5}}{3}$ 的底数为 $\frac{2}{3}$ ；⑤20200精确到千位为 $2 \times 1 0^{4}$ ；⑥若 $a b c > 0$ ，则 $\frac{| a |}{a} + \frac{b}{| b |} + \frac{| c |}{c} = 3$ 或 $- 1$ .其中一定正确的是（只需填写序号）.

查看试题解析
15. 2022年7月1日至8月31日，全国铁路累计发送旅客4.4亿人次.近似数4.4亿精确到位.

查看试题解析

三、解答题

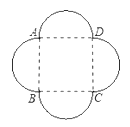
16. 如图，某花坛由四个半圆和一个正方形组成，已知正方形的面积为16cm² ，求该花坛的周长．（π=3.1415，计算结果保留三个有效数字）

查看试题解析
17. 观察：1+2=3=2²-1，1+2+2²=7=2³-1，1+2+2²+2³=15=2⁴-1，….又2³²约为4.3×10⁹ ，则1+2+2²+2³+…+2³¹约为多少?用科学记数法表示为a×10ⁿ的形式，并判断它是几位数.(a的值精确到0.1)

查看试题解析
18. 下列各数都是由四舍五入法得到的近似数，它们分别精确到哪一位？各有几个有效数字？
（1）小红的体重为45.0千克；
（2）小明的妈妈的年薪约为5万元；
（3）月球轨道呈椭圆形，远地点平均距离为4.055×10⁵千米．

查看试题解析
19. 世界上最大的沙漠──非洲的撒哈拉沙漠可以粗略地看成是一个长方形，撒哈拉沙漠的长度大约是5 149 900m，沙层的深度大约是366cm．已知撒哈拉沙漠中沙的体积约为33 345km³ ．请分别按下列要求取近似数．
（1）将撒哈拉沙漠的长度用科学记数法表示；
（2）将撒哈拉沙漠中沙层的深度四舍五入到10cm；
（3）将撒哈拉沙漠中沙的体积保留2个有效数字．

查看试题解析

四、综合题

20. 学习了无理数后，老师教了同学们一种估算无理数的近似值的新方法．
例如：估算 $\sqrt{13}$ 的近似值．

$∵ 3 = \sqrt{9} < \sqrt{13} < \sqrt{16} = 4$ ，

$∴$ 设 $\sqrt{13} = 3 + m$ ，显然 $0 < m < 1$ ，

$∴ {(\sqrt{13})}^{2} = {(3 + m)}^{2}$ ，

$∴ 13 = 9 + 6 m + m^{2}$ ，

$∴ 6 m = 4 - m^{2}$ ，

$∵ 0 < m < 1$ ，

$∴ 4 - 1 < 6 m < 4 - 0$ ，

$∴ 0.5 < m < 0.67$ ，

$∴ 3.5 < 3 + m < 3.67$ ．

故 $\sqrt{13}$ 的值在 $3.5$ 与 $3.67$ 之间．

问题：

(1)、请你依照上面的方法，估算 $\sqrt{43}$ 的近似值在与之间；

(2)、对于任意一个大于1的无理数 $\sqrt{a}$ ，若 $\sqrt{a}$ 的整数部分为 $b$ ，小数部分为 $m$ ，请用含 $a$ ， $b$ 的代数式表示 $m$ 的大致范围．

查看试题解析
21. 阅读材料，完成下列任务：
材料1：因为无理数是无限不循环小数，所以无理数的小数部分我们不可能全部写出来．比如： $π$ ， $\sqrt{2}$ 等，而常用的“…”或者“≈”的表示方法都不够百分百准确．
材料2：2.5的整数部分是2，小数部分是0.5，小数部分可以看成是 $2.5 - 2$ 得来的．
材料3：任何一个无理数，都夹在两个相邻的整数之间，如 $2 < \sqrt{5} < 3$ ，是因为 $\sqrt{4} < \sqrt{5} < \sqrt{9}$ ．
根据上述材料，回答下列问题：（参考值： $\sqrt{3} \approx 1.732$ ）

(1)、 $\sqrt{17}$ 的整数部分是，小数部分是．

(2)、 $5 + \sqrt{3}$ 也是夹在相邻两个整数之间的，可以表示为 $a < 5 + \sqrt{3} < b$ ，求 $a + b$ 的值．

(3)、已知 $3 + \sqrt{3} = x + y$ ，其中x是整数，且 $0 < y < 1$ ，求 $x + 4 y$ 的近似值（精确到0.1）．

查看试题解析

22. 李先生在2019年10月第2周星期五股市收盘时，以每股9元的价格买进某公司的股票1000股，在11月第2周的星期一至星期五，该股票每天收盘时每股的涨跌（单位：元）情况如下表：

时间	星期一	星期二	星期三	星期四	星期五
每股涨跌/元	0	-0.32	+0.47	-0.21	+0.56

注：表中记录的数据为每天收盘价格与前一天收盘价格的变化量，星期一的数据是与上星期五收盘价格的变化量．

(1)、请你判断在11月的第2周内，该股票价格收盘时，价格最高的是哪一天？

(2)、在11月第2周内，求李先生购买的股票每股每天平均的收盘价格．（结果精确到百分位）

查看试题解析

23. 体育委员统计了全班同学60秒跳绳的次数，并列出下面的频数分布表：
次数
60≤x＜90
90≤x＜120
120≤x＜150
150≤x＜180
180≤x＜210
频数
16
25
9
7
3

(1)、全班有多少同学？

(2)、组距是多少？组数是多少？

(3)、跳绳次数x在120≤x＜180范围的同学有多少？占全班同学的百分之几（精确到0.1%）？

查看试题解析

次数	60≤x＜90	90≤x＜120	120≤x＜150	150≤x＜180	180≤x＜210
频数	16	25	9	7	3