2023年浙教版数学九年级上册第二章 简单事件的概率 章末检测（提高版）
试卷更新日期：2023-07-02 类型：单元试卷
一、选择题（每题3分，共30分）
-
1. 如图，电路图上有3个开关A，B，C和一个小灯泡，同时闭合开关A，C或同时闭合开关B，C都可以使小灯泡发光.下列操作中，使“小灯泡发光”的事件是随机事件的是（ ）
A、不闭合开关 B、只闭合1个开关 C、只闭合2个开关 D、闭合3个开关2. 甲、乙、丙三人参加班级举行的“我爱家乡”演讲比赛，需要通过抽签方式来决定出场顺序，则出场顺序恰好是甲、乙、丙的概率是（ ）A、 B、 C、 D、3. 有三把不同的锁和四把钥匙，其中三把钥匙分别能打开三把锁，第四把钥匙不能打开这三把锁随机取出一把钥匙开任意一把锁，一次打开锁的概率是（ ）A、 B、 C、 D、4. 如图，电路图上有三个开关S1 ， S2 ， S3和两个小灯泡L1 ， L2 ， 随机闭合开关S1 ， S2 ， S3中的两个，能让灯泡L2发光的概率是（ ）
A、 B、 C、 D、5. 将一枚飞镖投掷到如图所示的正六边形镖盘上（每次飞镖均落在镖盘上，且落在镖盘的任何一个点的机会都相等），飞镖落在阴影区域的概率为（ ）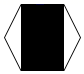
A、 B、 C、 D、6. 甲乙两人轮流在黑板上写下不超过
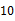的正整数（每次只能写一个数），规定禁止在黑板上写已经写过的数的约数，最后不能写的为失败者，如果甲写第一个，那么，甲写数字（ ）时有必胜的策略．
A、10 B、9 C、8 D、67. 同一元素中质子数相同，中子数不同的各种原子互为同位素，如与、与 ． 在一次制取的实验中，与的原子个数比为 ， 与的原子个数比为 ， 若实验恰好完全反应生成 ， 则反应生成的概率（ ）A、 B、 C、 D、8. 某小组做“用频率估计概率”的实验时，绘出的某一结果出现的频率分布折线图，则符合这一结果的实验可能是（ ）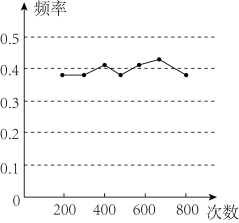
A、抛一枚均匀硬币，出现正面朝上 B、掷一个正六面体的骰子，出现2点朝上 C、从一个装有3个红球2个黑球的袋子中任取一球，取到的是黑球 D、一副去掉大小王的扑克牌洗匀后，从中任抽一张牌的花色是红桃9. 某口袋中有10个球，其中白球x个，绿球2x个，其余为黑球．甲从袋中任意摸出一个球，若为绿球则甲获胜，甲摸出的球放回袋中，乙从袋中摸出一个球，若为黑球则乙获胜，要使游戏对甲、乙双方公平，则x应该是（ ）A、3 B、4 C、1 D、210. 如图①所示，一张纸片上有一个不规则的图案（图中画图部分），小雅想了解该图案的面积是多少，她采取了以下的办法：用一个长为5m，宽为3m的长方形，将不规则图案围起来，然后在适当位置随机地向长方形区域扔小球，并记录小球在不规则图案上的次数（球扔在界线上或长方形区域外不计入试验结果），她将若干次有效试验的结果绘制成了图②所示的折线统计图，由此她估计此不规则图案的面积大约为（ ）
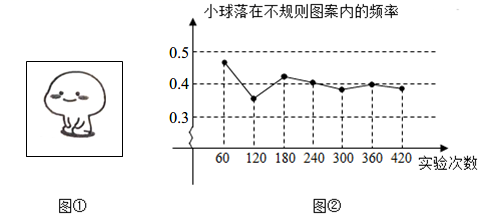A、6m2 B、5m2 C、4m2 D、3m2二、填空题（每空4分，共24分）
-
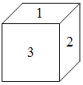
11. 有四张正面分别标有数字﹣4，﹣3，﹣2，1，的不透明卡片，它们除数字不同外其他全部相同，现将它们背面朝上，洗匀后从中抽取一张，将该卡片上的数字记为a，放回后洗匀，再从中抽取一张，将该卡片上的数字记为b，则a，b使得二次函数y＝x2﹣（a+5）x+3当x≤1时y随x的增大而减小，且一元二次方程（a+2）x2+bx+1＝0有解的概率为 ．12. 一个密码箱的密码，每个数位上的数都是从0到9的自然数，若要使不知道密码的人一次就拨对密码的概率小于 ，则密码的位数至少需要位．13. 在平面直角坐标系中,作OOAB,其中三个顶点分别是O(0,0),B(1,1),A( , ),其中点A,O,B不在同一直线上且-2≤ ≤2,-2≤ ≤2, , 均为整数，则所作OOAB为直角三角形的概率是.14. 如图，质地均匀的小立方体的一个面上标有数字1，两个面上标有数字2，三个面上标有数字3，抛掷这个小立方体，则向上一面的数字可能性最大的是.
15. 如图，转动三个可以自由转动的转盘（转盘均被等分），当转盘停止转动后，根据“指针落在灰色区域内”的可能性的大小，将转盘的序号按事件发生的可能性从大到小排列为 ．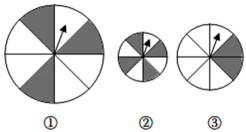
16. 一个不透明的袋中装有除颜色外大小形状都相同的三种球，其中红球、黄球、黑球的个数之比为 ． 从袋子中任意摸出1个球，结果是红球的概率为 ．三、综合题（共8题，共66分）
-
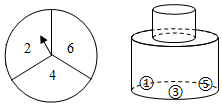
17. 有一个可自由转动的转盘，被分成了三个大小相同的扇形，分别标有数字2，4，6；另有一个不透明的瓶子，装有分别标有数字1，3，5的三个完全相同的小球．小明先转动一次转盘，停止后记下指针指向的数字（若指针指在分界线上则重转），小刚再从瓶子中随机取出一个小球，记下小球上的数字．若得到的两数字之和是3的倍数，则小明赢；若得到的两数字之和是7的倍数，则小刚赢，你认为这个游戏公平吗？请说明理由．
18. 2022年3月23日下午，“天宫课堂”第二课开讲，航天员翟志刚、王亚平、叶光富相互配合进行授课，激发了同学们学习航天知识的热情．小冰和小雪参加航天知识竞赛时，均获得了一等奖，学校想请一位同学作为代表分享获奖心得．小冰和小雪都想分享，于是两人决定一起做游戏，谁获胜谁分享，游戏规则如下：甲口袋装有编号为1，2的两个球，乙口袋装有编号为1，2，3，4，5的五个球，两口袋中的球除编号外都相同．小冰先从甲口袋中随机摸出一个球，小雪再从乙口袋中随机摸出一个球，若两球编号之和为奇数，则小冰获胜；若两球编号之和为偶数，则小雪获胜．请用列表或画树状图的方法，说明这个游戏对双方是否公平．
19. 小明与小刚做游戏，在甲、乙两个不透明的口袋中，分别装有完全一样的小球，其中甲口袋中的4个小球上分别标有数字1，2，3，4，乙口袋中的3个小球分别标有数字2，3，4，小明先从甲袋中随意摸出一个小球，记下数字为x，再从乙袋中随机摸出一个小球，记下数字为y．(1)、请用列表或画树状图的方法表示出所有可能出现的结果；(2)、若x，y都是方程的解时，则小明获胜；若x，y都不是方程的解时，则小刚获胜，它们谁获胜的概率大？请说明理由．20. 为缓减校园周边道路的交通压力，及时调整学生上学时间，某校需要了解本校学生的上学方式，学生可以从“：步行，：骑自行车，：乘坐公共交通，：家用汽车接送，：其他方式”．五个选项中进行选择．(1)、学生甲随机选择“：乘坐公共交通”方式的概率为 ．(2)、若两名学生分别从 ， ， ， ， 五种上学方式中随机选择一种，求两名学生一人选择“：步行”，另一人选择“：乘坐公共交通”的概率（请用画树状图或列表等方法说明理由）．21. 某学校为落实立德树人根本任务，使每个学生都能得到全面而个性的发展，特举办了“科学竞赛”活动，甲、乙两个班学生的成绩统计如下：分数/分
50
60
70
80
90
100
甲班人数/人
2
5
10
18
14
1
乙班人数/人
4
4
16
4
18
4
活动规定：以60分为及格线，并分别设置了一、二、三等奖，100分为一等奖，90分为二等奖，80分为三等奖．小亮分别计算了两个班的平均分和方差，得： ， ， ， ． 请你根据以上材料回答下列问题．
(1)、甲、乙两个班的中位数和众数分别是多少？(2)、你认为甲、乙两个班哪个班的成绩更优秀？为什么？(3)、该校从得100分的两男三女5人中，随机选取2人参加教育局组织的竞赛，请你用列表或画树状图的方法，求出恰好选取一男一女参赛的概率．22. 在一个不透明的布袋里装有4个标有1，2，3，4的小球，它们的形状、大小完全相同，小明从布袋里随机取出一个小球，记下数字为x，小红在剩下的3个小球中随机取出一个小球，记下数字为y.(1)、计算由x、y确定的点在函数的图象上的概率；(2)、小明和小红约定做一个游戏，其规则为：若x、y满足＞6则小明胜，若x、y满足＜6则小红胜，这个游戏公平吗？说明理由.若不公平，请写出公平的游戏规则.23. 如图，程序员在数轴上设计了A、B两个质点，它们分别位于-6和9的位置，现两点按照下述规则进行移动：每次移动的规则x分别掷两次正方体骰子，观察向上面的点数：
①若两次向上面的点数均为偶数，则A点向右移动1个单位，B点向左移2个单位；
②若两次向上面的点数均为奇数，则A点向左移动2个单位，B点向左移动5个单位；
③若两次向上面的点数为一奇一偶，则A点向右移动5个单位，B点向右移2个单位．
(1)、经过第一次移动，求B点移动到4的概率；(2)、从如图所示的位置开始，在完成的12次移动中，发现正方体骰子向上面的点数均为偶数或奇数，设正方体骰子向上面的点数均为偶数的次数为a，若A点最终的位置对应的数为b，请用含a的代数式表示b，并求当A点落在原点时，求此时B点表示的数；(3)、从如图所示的位置开始，经过x次移动后，若 ， 求x的值．24. 如图，地面上有一个不规则的封闭图形ABCD，为求得它的面积，小明设计了一个如下方法：①在此封闭图形内画出一个半径为1米的圆．
②在此封闭图形旁边闭上眼晴向封闭图形内掷小石子（可把小石子近似地看成点），记录如下：
掷小石子落在不规则图形内的总次数
50
150
300
500
…
小石子落在圆内（含圆上）的次数m
20
59
123
203
…
小石子落在圆外的阴影部分（含外缘）的次数n
29
91
176
293
…
m∶n
0.689
0.694
0.689
0.706
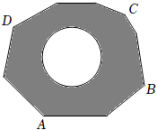(1)、通过以上信息，可以发现当投掷的次数很大时，则m∶n的值越来越接近（结果精确到0.1）．(2)、若以小石子所落的有效区域为总数（即m＋n），则随着投掷次数的增大，小石子落在圆内（含圆上）的频率值稳定在附近（结果精确到0.1）．(3)、请你利用（2）中所得频率的值，估计整个封闭图形ABCD的面积是多少平方米？（结果保留）