人教版八年级上册数学进阶课堂小测——12.2SAS判定全等三角形(三阶)
试卷更新日期:2023-07-02 类型:同步测试
一、选择题
-
1. 如图,在 中,已知 于点 , 平分 ,交 于点 ,过点 作 ,分别交 、 于点 、 , .则下列结论:① ;② ;③点 是 的中点;④ ;⑤ 为等边三角形.其中结论正确的个数是( )
 A、2 B、3 C、4 D、52. 如图所示,在平行四边形ABCD中,分别以AB、AD为边作等边△ABE和等边△ADF,分别连接CE,CF和EF,则下列结论,一定成立的个数是( )
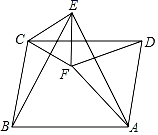
A、2 B、3 C、4 D、52. 如图所示,在平行四边形ABCD中,分别以AB、AD为边作等边△ABE和等边△ADF,分别连接CE,CF和EF,则下列结论,一定成立的个数是( )①△CDF≌△EBC;②△CEF是等边三角形;③∠CDF=∠EAF;④CE∥DF
 A、1 B、2 C、3 D、43. 以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
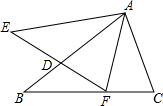
A、1 B、2 C、3 D、43. 以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )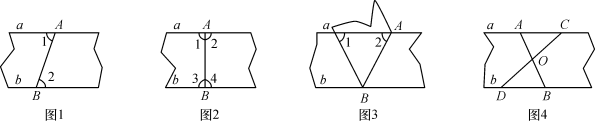 A、如图1,展开后,测得∠1=∠2 B、如图2,展开后,测得∠1=∠2,且∠3=∠4 C、如图3,测得∠1=∠2 D、如图4,展开后,再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD4. 如图,是的中线,E,F分别是和延长线上的点,且 , 连接 , , 下列说法:①和面积相等;②;③;④;⑤ . 其中正确的是( )
A、如图1,展开后,测得∠1=∠2 B、如图2,展开后,测得∠1=∠2,且∠3=∠4 C、如图3,测得∠1=∠2 D、如图4,展开后,再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD4. 如图,是的中线,E,F分别是和延长线上的点,且 , 连接 , , 下列说法:①和面积相等;②;③;④;⑤ . 其中正确的是( ) A、①② B、③⑤ C、①③④ D、①④⑤5. 如图,在3×3的正方形方格中,每个小正方形方格的边长都为1,则∠1和∠2的关系是( )
A、①② B、③⑤ C、①③④ D、①④⑤5. 如图,在3×3的正方形方格中,每个小正方形方格的边长都为1,则∠1和∠2的关系是( )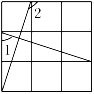 A、∠1=∠2 B、∠2=2∠1 C、∠2=90°+∠1 D、∠1+∠2=180°6. 如图,在四边形ABCD中,对角线AC平分∠BAD,AB>AD,下列结论正确的是( )
A、∠1=∠2 B、∠2=2∠1 C、∠2=90°+∠1 D、∠1+∠2=180°6. 如图,在四边形ABCD中,对角线AC平分∠BAD,AB>AD,下列结论正确的是( ) A、 B、 C、 D、的大小关系不确定7. 如图,在与中, , , , 点 , , 三点在同一条直线上,连接 , . 在以下判断中,错误的是( )
A、 B、 C、 D、的大小关系不确定7. 如图,在与中, , , , 点 , , 三点在同一条直线上,连接 , . 在以下判断中,错误的是( ) A、 B、 C、 D、8. 如图,在△ABC中,BD平分∠ABC,∠C=2∠CDB,AB=12,CD=3,则△ABC的周长为( )
A、 B、 C、 D、8. 如图,在△ABC中,BD平分∠ABC,∠C=2∠CDB,AB=12,CD=3,则△ABC的周长为( ) A、21 B、24 C、27 D、30
A、21 B、24 C、27 D、30二、填空题
-
9. 在△ABC中,AC=5,中线AD=7,则AB边的取值范围是.10. 如图,在中, , 于点D,于点C, . 点E,点F分别在线段上, , 连接 .
 (1)、图中与相等的线段是;(2)、当取最小值时°11. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=28°,∠2=30°,则∠3= .
(1)、图中与相等的线段是;(2)、当取最小值时°11. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=28°,∠2=30°,则∠3= .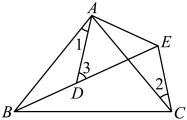 12. 如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.当∠A=40°时,则∠DEF的度数为 .
12. 如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.当∠A=40°时,则∠DEF的度数为 .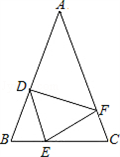 13. 如图,与中, , , , 交于D.给出下列结论:
13. 如图,与中, , , , 交于D.给出下列结论:①;②;③;④ .
其中正确的结论是(填写所有正确结论的序号).
三、解答题
-
14. (问题背景)
在四边形 中, , , , 、 分别是 、 上的点,且 ,试探究图1中线段 、 、 之间的数量关系.

(初步探索)
小晨同学认为:延长 到点 ,使 ,连接 ,先证明 ,再证明 ,则可得到 、 、 之间的数量关系是.
(探索延伸)
在四边形 中如图2, , , 、 分别是 、 上的点, ,上述结论是否仍然成立?说明理由.
(结论运用)
如图3,在某次南海海域军事演习中,舰艇甲在指挥中心( 处)北偏西30°的 处,舰艇乙在指挥中心南偏东70°的 处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以80海里/小时的速度前进,舰艇乙沿北偏东50°的方向以100海里/小时的速度前进1.2小时后,指挥中心观测到甲、乙两舰艇分别到达 , 处,且两舰艇之间的夹角( )为70°,试求此时两舰艇之间的距离.