人教版八年级上册数学进阶课堂小测——12.2SAS判定全等三角形（二阶）
试卷更新日期：2023-07-02 类型：同步测试
一、单选题
-
1. 如图，点P是∠BAC平分线AD上的一点，AC＝9，AB＝5，PB＝3，则PC的长不可能是（ ）
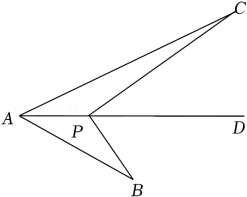A、4 B、5 C、6 D、72. 如图，在△ABC和△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，AD＜AB，且点E在线段CD上，则下列结论中不一定成立的是（ ）
A、△ABD≌△ACE B、BD⊥CD C、∠BAE-∠ABD=45° D、DE=CE3. 如图为6个边长相等的正方形组成的图形，则∠1+∠2+∠3的大小是（ ）
A、90° B、120° C、135° D、150°4. 如图，△ABC和△ADE中，AB=AC ， AD=AE ， ∠BAC=∠DAE ， 且点B ， D ， E在同一条直线上，若∠CAE+∠ACE+∠ADE=130°，则∠ADE的度数为（ ）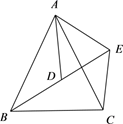
A、50° B、65° C、70° D、75°5. 对于任意△ （见示意图）．若 是△ 的边 上的中线， 、 的角平分线分别交 、 于点 ，连接 ，那么 之间的数量关系正确的是（ ）
A、 B、 C、 D、6. 如图，△ABC中，∠ABC=∠ACB，D为BC上一点，BF=CD，CE=BD，则∠EDF等于（ ）
A、 B、 C、 D、7. 下列命题：①相等的角是对顶角；
②两个全等三角形对应边上的中线相等；
③有两边和一角分别相等的两个三角形全等；
④锐角三角形的任意一个外角大于任何一个内角.
其中真命题的个数是（ ）
A、1个 B、2个 C、3个 D、4个8. 如图，在△ABC中AD是∠A的外角平分线，P是AD上一动点且不与点A，D重合，记AB＋AC＝a，PB＋PC＝b，则a、b的大小关系是（ ）
A、a＜b B、a＝b C、a＞b D、不能确定二、填空题
-
9. 如图，在△OAB和△OCD中，OA＝OB，OC＝OD，OA＞OC，∠AOB＝∠COD＝40°，连接AC，BD交于点M，连接OM.下列结论：①AC＝BD；②∠AMB＝40°；③OM平分∠BOC；④MO平分∠BMC.其中正确的是
10. 如图， ， ，且 ，则 .
11. 如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AB=10，AD平分∠CAB交BC于D点，E，F分别是AD，AC上的动点，则CE+EF的最小值为 ．
12. 在锐角△ABC中，∠ABC=60°，BC=2cm，BD平分∠ABC交AC于点D，点M，N分别是BD和BC边上的动点，则MN+MC的最小值是.
13. 如图，在锐角 中，AC＝10， ，∠BAC的平分线交BC于点D，点M，N分别是AD和AB上的动点，则BM＋MN的最小值是
14. 如图，在的正方形网格中标出了和 ， 则度.
三、解答题
