（华师大版）2023-2024学年八年级数学上册12.5 因式分解同步测试

试卷更新日期：2023-07-01 类型：同步测试

进入出卷网下载

一、选择题

1. 下列因式分解正确的是（）

A、 $2 a x^{2} - 4 a x = 2 a (x^{2} - 2 x)$ B、 $- a x^{2} + 4 a x - 4 a = - a {(x - 2)}^{2}$ C、 $x^{2} + 2 x y + 4 y^{2} = {(x + 2 y)}^{2}$ D、 $- m^{2} + n^{2} = (- m + n) (- m - n)$

查看试题解析
2. 下列多项式中，可以用平方差公式分解因式的是（）

A、x²＋1 B、－x²＋1 C、x²－2 D、－x²－1

查看试题解析
3. 已知 $a + b = 1 ， a b = - 6$ ，则 $a^{3} b - 2 a^{2} b^{2} + a b^{3}$ 的值为（）

A、57 B、120 C、 $- 39$ D、 $- 150$

查看试题解析
4. 下列因式分解正确的是（）

A、 $a^{2} b - a b^{2} = a (a + b) (a - b)$ B、 $a^{2} - 2 b^{2} = (a + 2 b) (a - 2 b)$ C、 $a^{3} - 2 a b + a b^{2} = a {(a - b)}^{2}$ D、 $a^{2} b^{2} - 4 a^{2} b + 4 a^{2} = a^{2} {(b - 2)}^{2}$

查看试题解析
5. 小强是一位密码编译爱好者，在他的密码手册中，有这样一条信息： $x - y$ ， $a - b$ ， 2， $x^{2} - y^{2}$ ， $a$ ， $x + y$ ，分别对应下列六个字：华、我、爱、美、游、中，现将 $2 a (x^{2} - y^{2}) - 2 b (x^{2} - y^{2})$ 因式分解，结果呈现的密码信息可能是（）

A、爱我中华 B、我游中华 C、中华美 D、我爱游

查看试题解析
6. 已知a、b、c是三角形的边长，那么代数式 ${(a - b)}^{2} - c^{2}$ 的值是（）

A、小于零 B、等于零 C、大于零 D、大小不确定

查看试题解析
7. 对于① $a - 2 a b = a (1 - 2 b)$ ， ② $(a + 2) (a - 1) = a^{2} + a - 2$ ，从左到右的变形，表述正确的是（）

A、①是因式分解，②是乘法运算 B、①是乘法运算，②是因式分解 C、①②都是因式分解 D、①②都是乘法运算

查看试题解析
8. 下列多项式中，能因式分解得到（x+y）(x-y)的是（　　）

A、x²+y² B、x²-y² C、-x²-y² D、-x²+y²

查看试题解析
9. 将几个图形拼成一个新的图形，再通过两种不同的方法计算同一个图形的面积，可以得到一个等式．例如，由图（1）可得等式： $x^{2} + (p + q) x + p q = (x + p) (x + q)$ ．将图（2）所示的卡片若干张进行拼图，可以将二次三项式 $a^{2} + 3 a b + 2 b^{2}$ 分解因式为（）

A、 $(a + b) (2 a + b)$ B、 $(a + b) (3 a + b)$ C、 $(a + b) (a + 2 b)$ D、 $(a + b) (a + 3 b)$

查看试题解析
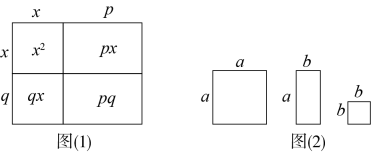10. 篮子里有若干苹果，可以平均分给 $(x + 1)$ 名同学，也可以平均分给 $(x - 3)$ 名同学（x为大于3的正整数），用代数式表示苹果数量不可能的是（）

A、 $2 x^{3} - 4 x^{2} - 6 x$ B、 $x^{3} - 2 x - 3$ C、 $3 (x + 1) (x - 3)$ D、 $x (x^{2} - 2 x - 3)$

查看试题解析

二、填空题

11. 已知mn＝4，n-m＝3，则mn²-m²n＝.

查看试题解析
12. 分解因式： $- a^{2} + 4 b^{2} =$ .

查看试题解析
13. 在实数范围内分解因式： $x^{2} - 2 x - 2 =$ .

查看试题解析
14. 把多项式 $6 x^{3} y^{3} - 3 x^{2} y^{3}$ 分解因式时，应提取的公因式是．

查看试题解析
15. 一个长方形的长与宽分别为a，b，若周长为12，面积为5，则 $a b^{3} + 2 a^{2} b^{2} + a^{3} b$ 的值为．

查看试题解析

三、解答题

16. 已知 $a$ ， $b$ ， $c$ 为正数，满足如下两个条件：
$a + b + c = 32$ ①
$\frac{b + c - a}{b c} + \frac{c + a - b}{c a} + \frac{a + b - c}{a b} = \frac{1}{4}$ ②
证明：以 $\sqrt{a}$ ， $\sqrt{b}$ ， $\sqrt{c}$ 为三边长可构成一个直角三角形.

查看试题解析
17. 在 $(x^{2} - 2 x + a) (3 x + b)$ 的运算结果中， $x^{2}$ 的系数为-4，x的系数为-7，求a，b的值并对式子 $4 a x^{2} + b^{2}$ 进行因式分解．

查看试题解析
18.
（Ⅰ）先化简，再求值： $[(2 a + b)^{2} + (b + 2 a) (b - 2 a) - 2 b (a + 2 b)] \div 2 b$ ，其中 $a = \frac{1}{2}$ ， $b = \frac{1}{3}$ ；
（Ⅱ）分解因式：① $x^{3} - 9 x$ ；② $6 x y^{2} - 9 x^{2} y - y^{3}$ ．

查看试题解析
19. 第一环节：自主阅读材料：
常用的分解因式方法有提公因式、公式法等．但有的多项式只用上述方法就无法分解，如x²-4y²+2x-4y，细心观察这个式子会发现前两项符合平方差公式，后两项可提取公因式，分解过程为：

x²-4y²+2x-4y

=(x²-4y²)+(2x-4y) ……分组

=(x-2y)(x+2y)+2(x-2y) ……组内分解因式

=(x-2y)(x+2y+2) ……整体思想提公因式

这种分解因式的方法叫分组分解法。

第二环节：利用这种方法解决下列问题。

因式分解：x²y-4y-2x²+8．

第三环节：拓展运用。

已知a，b，c为△ABC的三边，且b²+2ab=c²+2ac，试判断△ABC的形状．

查看试题解析

四、综合题

20. 若一个四位自然数n的千位数字与十位数字相同，百位数字与个位数字相同，则称n为“间隔数”.将“间隔数”n的千位、百位数字交换，十位、个位数字交换，得到一个新的“间隔数” $n^{'}$ ，记 $F (n) = \frac{n + n^{'}}{101}$ .

(1)、求 $F (1919)$ ， $F (8787)$ ；

(2)、求证：对任意一个“间隔数” $n$ ， $F (n)$ 能被11整除.

查看试题解析

（华师大版）2023-2024学年八年级数学上册12.5 因式分解 同步测试

一、选择题

二、填空题

三、解答题

四、综合题

（华师大版）2023-2024学年八年级数学上册12.5 因式分解同步测试