陕西省西安市高陵区2022-2023学年八年级下册第二次月考数学试卷

试卷更新日期：2023-07-01 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列各式 $- x ， \frac{2}{π} ， - \frac{3}{x - 2} ， \frac{x}{x^{2} - 1}$ 中，分式有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列选项中，从左到右的变形是因式分解的是（）

A、 $(b + 1) (b - 1) = b^{2} - 1$ B、 $a^{2} - a - 2 = (a - 1) (a + 2)$ C、 $a^{2} - 4 = (a + 2) (a - 2)$ D、 $x^{2} - x - 3 = x (x - 1) - 3$

查看试题解析
3. 若把分式 $\frac{2 x}{y}$ 中x和y的值都扩大3倍，则分式的值（）

A、不变 B、扩大为原来的3倍 C、缩小为原来的 $\frac{1}{3}$ D、扩大为原来的9倍

查看试题解析
4. 下列化简正确的是（）

A、 $\frac{a^{2} + b^{2}}{a + b} = a + b$ B、 $\frac{- a - b}{a + b} = - 1$ C、 $\frac{- a - b}{a - b} = - 1$ D、 $\frac{a^{2} - b^{2}}{a - b} = a - b$

查看试题解析
5. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B = 30 °$ ， D为 $B C$ 上一点， $C D = A D = 2$ ，则 $B C$ 的长为（）

A、8 B、7 C、6 D、5

查看试题解析
6. 若 $x^{2} + 2 (m - 5) x + 16$ 是完全平方式，则m的值为（）

A、1 B、4 C、9 D、1或9

查看试题解析
7. 《九章算术》中有一道关于古代驿站送信的题目，其白话译文为：一份文件，若用慢马送到800里远的城市，所需时间比规定时间多1天；若改为快马派送，则所需时间比规定时间少2天，已知快马的速度是慢马的 $\frac{5}{2}$ 倍，求规定时间.设规定时间为 $x$ 天，则下列列出的分式方程正确的是（）

A、 $\frac{800}{x + 2} = \frac{5}{2} \times \frac{800}{x - 1}$ B、 $\frac{800}{x - 1} = \frac{5}{2} \times \frac{800}{x + 2}$ C、 $\frac{800}{x - 2} = \frac{5}{2} \times \frac{800}{x + 1}$ D、 $\frac{800}{x + 1} = \frac{5}{2} \times \frac{800}{x - 2}$

查看试题解析
8. 如图，在平面直角坐标系中，将 $△ A B C$ 绕点 $C (0 ， - 2)$ 旋转 $180 °$ 得到 $△ A_{1} B_{1} C$ ，设点 $A_{1}$ 的坐标为 $(a ， b)$ ，则点A的坐标为（）

A、 $(- a ， - b + 4)$ B、 $(- a + 4 ， - b)$ C、 $(- a - 4 ， - b)$ D、 $(- a ， - b - 4)$

查看试题解析

二、填空题

9. 若使分式 $\frac{x}{x - 3}$ 有意义，则x的取值范围是．

查看试题解析
10. 若 $m^{2} - n^{2} = 28$ ， $m + n = 7$ ，则 $m - n =$ ．

查看试题解析
11. 边长为a，b的长方形如图所示，若它的周长为 $2 \sqrt{5}$ ，面积为 $\sqrt{5}$ ，则 $a^{2} b + a b^{2}$ 的值为．

查看试题解析
12. 若关于 $x$ 的分式方程 $\frac{2 - m}{1 - x} = 1$ 无解，则 $m =$ ．

查看试题解析
13. 如图， $A D$ 是 $△ A B C$ 的角平分线， $D E ⊥ A B$ 于点E， $S_{△ A B C} = 36$ ， $D E = 4$ ， $A C = 8$ ，则 $A B$ 的长是．

查看试题解析

三、解答题

14. 分解因式： $2 x^{2} - 8$

查看试题解析
15. 计算： $\frac{m^{2}}{m - 1} + \frac{1}{1 - m}$ ．

查看试题解析
16. 解方程： $\frac{x - 3}{x - 2} + 1 = \frac{3}{2 - x}$

查看试题解析
17. 如图，在 $△ A B C$ 中，点E在边 $A B$ 上，且 $C E = B C$ ，请用尺规作图法，求作将 $△ A B C$ 绕点C顺时针旋转得到的 $△ D E C$ ，其中点E与点B对应．（保留作图痕迹，不写作法）

查看试题解析
18. 解不等式组 ${\begin{array}{l} 3 x < x + 2 ① ， \\ 8 - x \geq 1 - 3 (x - 1) ② ， \end{array}$ 并把解集在数轴上表示出来．

查看试题解析
19. 先化简： $\frac{x^{2} - 4 x + 4}{x^{2} - 2 x} \div (x - \frac{4}{x})$ ，若 $- 3 < x < 3$ ，请选取一个合适的整数作为x的值代入求值．

查看试题解析
20. 若a，b，c分别为 $△ A B C$ 三边的长，且满足 $b (a - b) - c (b - a) = 0$ ，试判断 $△ A B C$ 的形状，并说明理由．

查看试题解析
21. 我们知道图形是一种重要的数学语言，它直观形象，能有效地表现代数中一些重要的数量关系．认真观察下面两个拼图，列出等量关系式表示阴影部分的面积．

(1)、图1表示的等量关系式可以是；图2表示的等量关系式可以是．

(2)、已知 $a - b = 2$ ， $a^{2} + b^{2} = 34$ ，求 $a b$ 的值．

查看试题解析
22. 数式规律
观察以下等式：

第1个等式： $\frac{1}{3} \times (1 + \frac{2}{1}) = 2 - \frac{1}{1}$ ；

第2个等式： $\frac{5}{5} \times (1 + \frac{2}{3}) = 2 - \frac{1}{3}$ ；

第3个等式： $\frac{9}{7} \times (1 + \frac{2}{5}) = 2 - \frac{1}{5}$ ；

第4个等式： $\frac{13}{9} \times (1 + \frac{2}{7}) = 2 - \frac{1}{7}$ ；

第5个等式： $\frac{17}{11} \times (1 + \frac{2}{9}) = 2 - \frac{1}{9}$ ；

…

按照以上规律，解决下列问题：

(1)、写出第6个等式：；

(2)、写出你猜想的第n个等式：（用含n的等式表示），并证明．

查看试题解析
23. 如图所示，△ACB和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°，D为AB边上一点．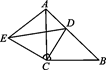

(1)、求证：△ACE≌△BCD；

(2)、若AD＝5，BD＝12，求DE的长．

查看试题解析
24. 教育部印发的《义务教育课程方案（2022年版）》，将劳动从原来的综合实践活动课程中独立出来．某中学为了让学生体验农耕劳动，开辟了一处耕种园，需要采购一批菜苗开展种植活动．据了解，市场上每捆A种菜苗的价格是菜苗基地的1.5倍，用300元在市场上购买的A种菜苗比在菜苗基地购买的少5捆．

(1)、求菜苗基地每捆A种菜苗的价格．

(2)、菜苗基地每捆B种菜苗的价格是30元，学校决定在菜苗基地购买A，B两种菜苗共100捆，所花的费用不超过2400元，求在菜苗基地购买A种菜苗至少多少捆．

查看试题解析
25. 某数学老师在讲因式分解时，为了提高同学们的思维能力，他补充了一道这样的题：对多项式 $(a^{2} + 4 a + 2) (a^{2} + 4 a + 6) + 4$ 进行因式分解．有个学生解答过程如下：
解：设 $a^{2} + 4 a = b$ ．
原式 $= (b + 2) (b + 6) + 4$ 第一步
      $= b^{2} + 8 b + 16$ 第二步
      $= {(b + 4)}^{2}$ 第三步
      $= {(a^{2} + 4 a + 4)}^{2}$ 第四步
根据以上解答过程回答下列问题：

(1)、该同学第二步到第三步运用了因式分解的哪种方法？____（填选项）．

A、提取公因式 B、平方差公式 C、两数和的完全平方公式 D、两数差的完全平方公式

(2)、对第四步的结果继续因式分解得到结果为．

(3)、请你模仿以上方法对多项式 $(x^{2} - 6 x) (x^{2} - 6 x + 18) + 81$ 进行因式分解．

查看试题解析
26. 如图，在平面直角坐标系中，点A的坐标为 $(0 ， a)$ ，点B的坐标为 $(b + 3 ， b)$ ，且a，b满足 $| a - 3 | + b^{2} + 2 b + 1 = 0$ ．

(1)、求A，B两点的坐标．

(2)、点C在第一象限内， $A C ∥ x$ 轴，将线段 $A B$ 进行适当的平移得到线段 $D C$ ，点A的对应点为点D，点B的对应点为点C，连接 $A D$ ，若 $△ A C D$ 的面积为12，求线段 $A C$ 的长．

(3)、P为x轴上一个动点，连接 $A P ， B P$ ，若 $△ P A B$ 是以 $A B$ 为直角边的直角三角形，请直接写出P点的坐标．

查看试题解析