江苏省宜兴市丁蜀学区2022-2023学年八年级下学期第二次课堂练习数学试卷

试卷更新日期：2023-07-01 类型：月考试卷

进入出卷网下载

一、单选题(共30分）

1. 下列二次根式中，最简二次根式是（）

A、 $- \sqrt{3}$ B、 $\sqrt{20}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{a^{2}}$

查看试题解析
2. 下列调查适合抽样调查的是（）

A、审核书稿中的错别字 B、调查某批汽车的抗撞击能力 C、了解八名同学的视力情况 D、对飞机零部件安全性的调查

查看试题解析
3. 如图，在四边形ABCD中，AB=CD，BC=AD，若∠D=120°，则∠C的度数为（）

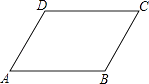A、60° B、70° C、80° D、90°

查看试题解析
4. 下列各式错误的是（）

A、 $5 = {(\sqrt{5})}^{2}$ B、 $5 = {\sqrt{{(- 5)}^{2}}}^{}$ C、 $5 = {(- \sqrt{5})}^{2}$ D、 $5 = {(\sqrt{- 5})}^{2}$

查看试题解析
5. 下列两个图形，可以组成平行四边形的是（）

A、两个等腰三角形 B、两个直角三角形 C、两个锐角三角形 D、两个全等三角形

查看试题解析
6. 如图，四边形 $A B C D$ 是平行四边形，下列说法能判定四边形 $A B C D$ 是菱形的是（）

A、 $A C ⊥ B D$ B、 $B A ⊥ A C$ C、 $A B = C D$ D、 $∠ B A D = ∠ A B C$

查看试题解析
7. 下列式子从左到右的变形一定正确的是（）

A、 $\frac{a + 3}{b + 3}$ = $\frac{a}{b}$ B、 $\frac{a}{b}$ = $\frac{a c}{b c}$ C、 $\frac{3 a}{3 b}$ = $\frac{a}{b}$ D、 $\frac{a}{b}$ = $\frac{a^{2}}{b^{2}}$

查看试题解析
8. 如图，在平面直角坐标系中，将一块含有 $45 °$ 角的直角三角板按如图所示的方式放置，直角顶点C的坐标为(2，0)，顶点A的坐标为(0，4)，顶点B恰好落在第一象限内，反比例函数 $y = \frac{k}{x}$ 的图像经过点B，则k的值为（）

A、4 B、6 C、8 D、12

查看试题解析
9. 在函数y＝ $\frac{\sqrt{x + 2}}{3 x}$ 中，自变量x的取值范围是（　　）

A、x≥﹣2且x≠0 B、x≤2且x≠0 C、x≠0 D、x≤﹣2

查看试题解析
10. 已知反比例函数y= $\frac{2}{x}$ 和正比例函数y= $\frac{1}{2} x$ 的图像交于点M，N，动点P(m，0)在x轴上.若△PMN为锐角三角形，则m的取值为（）

A、-2＜m＜ $\sqrt{5}$ 且m≠0 B、- $\sqrt{5}$ ＜m＜ $\sqrt{5}$ 且m≠0 C、- $\frac{5}{2}$ ＜m＜- $\sqrt{5}$ 或 $\sqrt{5}$ ＜m＜ $\frac{5}{2}$ D、-2＜m＜- $\sqrt{5}$ 或 $\sqrt{5}$ ＜m＜2

查看试题解析

二、填空题(共24分）

11. 小明、小红、小亮三名同学想要了解本市老年人的健康状况，他们各自进行了如下调查．
小明；周末去医院随机询问了100个老年人的健康状况．
小红：放学之后去广场上随机询问了100名跳广场舞的老年人的健康状况．
小亮：放学后在本市区随机询问了100名老年人的健康状况．
他们三个的调查结果，同学的更可靠．（填“小明”“小红”或“小亮”）

查看试题解析
12. 若分式 $\frac{1}{x}$ 有意义，则x的取值范围是.

查看试题解析
13. 如图，在平行四边形ABCD中， $A B = 5$ ， CE平分 $∠ B C D$ 交AD边于点E，且 $A E = 2$ ，则BC的长为．

查看试题解析
14. 在一个不透明的袋子中装有仅颜色不同的8个球，其中红球3个，黄球5个．请你从袋子中取出m个红球，再从袋子中随机摸出一个球，将“摸出的球为黄色”记为事件A，若此事件为必然事件，则m的值为．

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ B A C = 130 °$ ，将 $△ A B C$ 绕点 $C$ 逆时针旋转得到 $△ D E C$ ，点 $A$ ， $B$ 的对应点分别为 $D$ ， $E$ ，连接 $A D$ ．当点 $A$ ， $D$ ， $E$ 在同一条直线上时，则旋转角 $∠ A C D$ 的度数为．

查看试题解析
16. 已知直角三角形的两直角边a、b满足 $\sqrt{a - 5} + | b - 12 | = 0$ ，则斜边c上的中线长为．

查看试题解析
17. 如图，边长为2的正方形 $A B C D$ 的对角线相交于点O，点E是 $B C$ 边上的动点，连接 $O E$ 并延长交 $A B$ 的延长线于点P，过点O作 $O Q ⊥ O P$ 交 $C D$ 于点F，交 $B C$ 延长线于点Q，连接 $P Q$ ．若点 $E$ 恰好是 $O P$ 中点时，则 $P Q =$ ．

查看试题解析
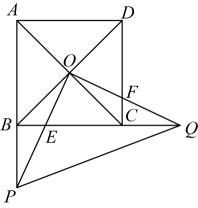18. 如图，已知正方形ABCD中，AD=6，∠DAE=30°，点F为AE的中点，过点F作直线分别与AD、BC相交于点M、N，若MN=AE，则AM的长等于．

查看试题解析

三、解答题(66分）

19. 计算

(1)、 $4 \sqrt{2} + \sqrt{8} - \sqrt{18}$

(2)、 $\sqrt{1 \frac{1}{3}} \div \sqrt{2 \frac{1}{3}} \times \sqrt{1 \frac{2}{5}}$

查看试题解析
20. 解方程

(1)、 $\frac{5 x - 4}{x - 2} = \frac{4 x + 10}{3 x - 6} - 1$

(2)、 $1 - \frac{x - 2}{2 + x} = \frac{16}{x^{2} - 4}$

查看试题解析
21. 先化简，再求值： $\frac{m^{2}}{1 - m^{2}} \cdot (1 - \frac{1}{m})$ ，其中m＝2.

查看试题解析
22. 学校就“我最喜爱的课外读物”从文学、艺术，科普和其他四个类别进行了抽样调查（每位同学只选一类），如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息，解答下列问题：

(1)、本次调查中，一共调查了多少名同学；

(2)、求条形统计图中m，n的值；

(3)、扇形统计图中，求艺术类读物所在扇形的圆心角的度数.

查看试题解析
23. 如图，在平行四边形ABCD中，对角线AC，BD相交于点O，且AE=CF，则四边形DEBF是平行四边形吗?说明理由.

查看试题解析
24. 已知一次函数 $y_{1} = k x + b (k \neq 0)$ 的图象与反比例函数 $y_{2} = \frac{m}{x} (m \neq 0)$ 的图象交于A、B两点，与x轴交于点C，已知点 $A (1 ， 4)$ ，点B的横坐标为 $- 2$ ．

(1)、求一次函数与反比例函数的表达式，并在图中画出一次函数的图象；

(2)、D为x轴上一点，若 $△ A B D$ 的面积为6，求点D的坐标；

(3)、根据函数图象，直接写出不等式 $y_{1} \leq y_{2}$ 的解集．

查看试题解析
25. 如图，在平面直角坐标系 $x O y$ 中，函数 $y = - x + 5$ 的图象与函数 $y = \frac{k}{x} (k < 0)$ 的图象相交于点A，并与 $x$ 轴交于点C，S_△_AOC=15．点D是线段AC上一点，CD：AC=2：3．

(1)、求 $k$ 的值；

(2)、求点D的坐标；

(3)、根据图象，直接写出当 $x < 0$ 时不等式 $\frac{k}{x} + x > 5$ 的 $x$ 的解集．

查看试题解析
26. 瑞兔迎春，福满万家吉祥物“兔圆圆”拉开2023央视总台兔年春晚的帷幕．竖直的耳朵、微昂的脑袋、挺起的胸脯等设计巧思，彰显出奋进向上的精气神，某商店用1500元购进了一批“兔圆圆”玩具，过了一段时间，又用3500元购进一批“兔圆圆”玩具，所购数量是第一次购进数量的2倍，但每个“兔圆圆”玩具的价格比第一次购进的价格贵了5元．

(1)、商店第一次购进“兔圆圆”玩具多少个？

(2)、若该商店两次购进的“兔圆圆”玩具按相同的标价销售，全部售完后利润不低于1150元，则每个“兔圆圆”玩具的标价至少是多少元？

查看试题解析
27. 在长方形 $A B C D$ 中， $∠ A = ∠ B = ∠ C = ∠ D = 90 °$ ， $A B = C D = 5$ ， $B C = A D = 4$ ．

(1)、如图1， $P$ 为 $B C$ 边上一点，将 $△ A B P$ 沿直线 $A P$ 翻折至 $△ A P Q$ 的位置，其中点 $Q$ 是点 $B$ 的对称点，当点 $Q$ 落在 $C D$ 边上时，求 $D Q$ 的长。

(2)、如图2，点 $M$ 是射线 $A B$ 上的一个动点，将 $△ A D M$ 沿 $D M$ 翻折，其中点 $A$ 的对称点为 $A^{'}$ ，当 $A^{'}$ ， $M$ ， $C$ 三点在同一直线上时，请直接写出 $A M$ 的长．

查看试题解析
28. 如图，四边形ABCD为正方形，DE∥AC且CE＝CA，直线EC交DA延长线于F.

(1)、若CD＝6，求DE的长；

(2)、求证：AE＝AF.

查看试题解析