广东省广州市黄埔区2023年高三模拟考试数学试卷
试卷更新日期:2023-06-30 类型:高考模拟
一、单选题
-
1. 设复数满足(是虚数单位),则( )A、 B、 C、 D、2. 设集合 , , 则( )A、 B、 C、 D、3. 用一个平行于圆锥底面的平面去截圆锥,截得的圆台上底面半径为1,下底面半径为2,且该圆台侧面积为 , 则原圆锥的母线长为( )A、2 B、 C、4 D、4. 函数的大致图象是( ).A、
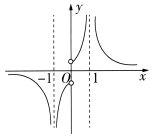 B、
B、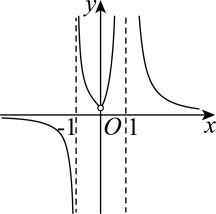 C、
C、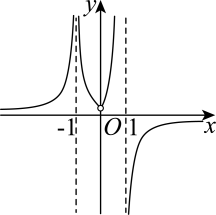 D、
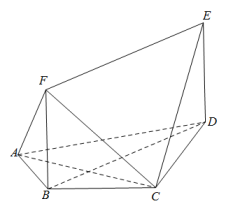
D、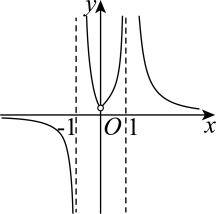 5. 南宋数学家杨辉在《详解九章算法》中,研究了二阶等差数列.若是公差不为零的等差数列,则称数列为二阶等差数列.现有一个“三角垛”,共有40层,各层小球个数构成一个二阶等差数列,第一层放1个小球,第二层放3个小球,第三层放6个小球,第四层放10个小球, , 则第40层放小球的个数为( )A、1640 B、1560 C、820 D、7806. 若双曲线的两条渐近线与椭圆:的四个交点及椭圆的两个焦点恰为一个正六边形的顶点,则椭圆的离心率为( )A、 B、 C、 D、7. 已知可导函数的导函数为 , 若对任意的 , 都有 , 且为奇函数,则不等式的解集为( )A、 B、 C、 D、8. 我国南北朝时期的伟大科学家祖暅于5世纪末提出了下面的体积计算原理:“幂势既同,则积不容异”.这就是“祖暅原理”.祖暅原理用现代语言可描述为:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.运用祖暅原理计算球的体积时,构造一个底面半径和高都与球的半径相等的圆柱,与半球(如图1)放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥后得到一新几何体(如图2),用任何一个平行于底面的平面去截它们时,可证得所截得的两个截面的面积都相等,由此得到新几何体与半球的体积相等,即 . 现将椭圆绕轴旋转一周后得到如图3所示的椭球,类比上述方法,运用祖暅原理可求得该椭球的体积为( )
5. 南宋数学家杨辉在《详解九章算法》中,研究了二阶等差数列.若是公差不为零的等差数列,则称数列为二阶等差数列.现有一个“三角垛”,共有40层,各层小球个数构成一个二阶等差数列,第一层放1个小球,第二层放3个小球,第三层放6个小球,第四层放10个小球, , 则第40层放小球的个数为( )A、1640 B、1560 C、820 D、7806. 若双曲线的两条渐近线与椭圆:的四个交点及椭圆的两个焦点恰为一个正六边形的顶点,则椭圆的离心率为( )A、 B、 C、 D、7. 已知可导函数的导函数为 , 若对任意的 , 都有 , 且为奇函数,则不等式的解集为( )A、 B、 C、 D、8. 我国南北朝时期的伟大科学家祖暅于5世纪末提出了下面的体积计算原理:“幂势既同,则积不容异”.这就是“祖暅原理”.祖暅原理用现代语言可描述为:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.运用祖暅原理计算球的体积时,构造一个底面半径和高都与球的半径相等的圆柱,与半球(如图1)放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥后得到一新几何体(如图2),用任何一个平行于底面的平面去截它们时,可证得所截得的两个截面的面积都相等,由此得到新几何体与半球的体积相等,即 . 现将椭圆绕轴旋转一周后得到如图3所示的椭球,类比上述方法,运用祖暅原理可求得该椭球的体积为( )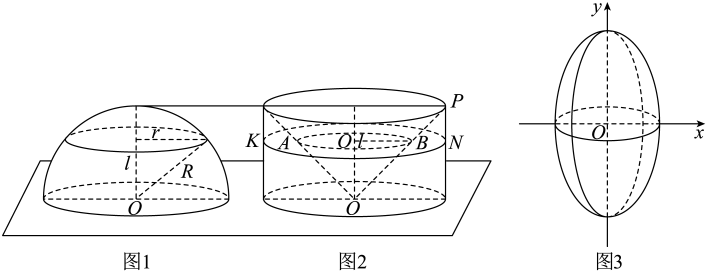 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 已知向量 , , 则( )A、 B、 C、 D、在上的投影向量是10. 下列说法正确的是( )A、若 , 则随机变量的方差 B、若 , , 则 C、若随机事件满足 , , , 则 D、数据5,7,8,11,13,15,17的第80百分位数为1511. 已知函数 , 则下列说法正确的是( )A、 B、函数的最小正周期为 C、函数的图象的对称轴方程为 D、函数的图象可由的图象向左平移个单位长度得到12. 已知函数 , 且 , , 则下列结论正确的是( )A、 B、 C、在上单调递减 D、最小值为
三、填空题
-
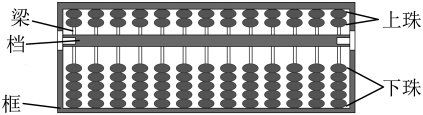
13. 的展开式中的系数是(用数字作答).14. 写出经过点且被圆截得的弦长为的一条直线的方程 .15. 算盘是中国传统的“珠算”工具.下图是一把算盘,自右向左,分别是个位、十位、百位、 , 上面一粒珠(简称上珠)代表数字 , 下面一粒珠(简称下珠)代表数字 , 即五粒下珠的大小等于同组一粒上珠的大小.现从个位和十位这两组中随机选择往下拨一粒上珠,往上拨粒下珠,则算盘表示的数为质数(除了和本身没有其它的约数)的概率是.
四、双空题
-
16. 的内角的对边分别为 , 若 , 则 , 的最大值是 .
五、解答题
-
17. 在△中,角的对边分别为 , 且 , , 设与的夹角为 .(1)、当时,求及△的面积;(2)、再从条件①、条件②这两个条件中选择一个作为已知,求函数的最大值与最小值.
条件①:;条件②: .
注:如果选择条件①和条件②分别解答,按第一个解答计分.
18. 某校为了丰富学生课余生活,组建了足球社团.足球社团为了解学生喜欢足球是否与性别有关,随机抽取了男、女同学各100名进行调查,得到如下列联表:喜欢足球
不喜欢足球
合计
男生
60
40
100
女生
30
70
100
合计
90
110
200
(1)、根据小概率值的独立性检验,判断是否有的把握认为该校学生喜欢足球与性别有关?(2)、现从喜欢足球的学生中抽取了2名男生和1名女生示范点球射门.已知男生进球的概率为 , 女生进球的概率为 , 每人射门一次,假设各人射门相互独立,求3人进球总次数的分布列和均值.附: , .
19. 已知数列的前项和为 , 且 , , .(1)、求数列的通项公式;(2)、设 , 数列的前项和 , 求证: .
-