人教A版（2019）必修二10.1.3古典概型

试卷更新日期：2023-06-30 类型：单元试卷

进入出卷网下载

一、选择题（共11题）

1. ”微信抢红包”自2015年以来异常火爆，在某个微信群某次进行的抢红包活动中，若所发红包的总金额为8元，被随机分配成1.72元，1.83元，2.28元，1.55元，0.62元，共5份，供甲、乙等5人抢，每人只能抢一次，则甲、乙二人抢到的金额之和不低于3.5元的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
2. 我省高考从2021年开始实行 $3 + 1 + 2$ 模式，“3”为全国统考科目语文、数学、外语，所有学生必考；“1”为首选科目，考生须在物理、历史两科中选择一科；“2”为再选科目，考生可在化学、生物、思想政治、地理4个科目中选择两科，今年某校高一的学生小霞和小芸正准备进行选科，假如她们首选科目都是历史，再选科目她们选择每个科目的可能性均等，且她俩的选择互不影响，则她们的选科至少有一科不相同的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{2}$ C、 $\frac{5}{6}$ D、 $\frac{3}{4}$

查看试题解析
3. 在1， 2， 3， 6这组数据中随机取出三个数，则数字2是这三个不同数字的平均数的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
4. nbsp；2019年5月22日具有“国家战略”意义的“长三角一体化”会议在芜潮举行，长三角城市群包括，上海市以及江苏省、浙江省、安徽省三省部分城市，简称“三省一市”．现有4名高三学生准备高考后到上海市、江苏省、浙江省、安徽省四个地方旅游，假设每名同学均从这四个地方中任意选取一个去旅游则恰有一个地方未被选中的概率为（）

A、 $\frac{27}{64}$ B、 $\frac{9}{16}$ C、 $\frac{81}{256}$ D、 $\frac{7}{16}$

查看试题解析
5. 甲盒中有200个螺杆，其中有 $x$ 个 $A$ 型的，乙盒中有240个螺母，其中有 $y$ 个 $A$ 型的．今从甲、乙两盒中各任取一个，不能配成 $A$ 型螺栓的概率为 $\frac{2}{5}$ ，则恰好可配成 $A$ 型螺栓的概率为（）

A、 $\frac{1}{20}$ B、 $\frac{15}{16}$ C、 $\frac{3}{5}$ D、 $\frac{19}{20}$

查看试题解析
6. 在5件产品中，有4件正品，从中任取2件，2件都是正品的概率是（）

A、 $\frac{4}{5}$ B、 $\frac{1}{5}$ C、 $\frac{3}{5}$ D、 $\frac{2}{5}$

查看试题解析
7. 在5件产品中，有3件一等品和2件二等品，从中任取2件，以 $\frac{7}{10}$ 为概率的事件是（）

A、恰有1 件一等品 B、至少有1件一等品 C、至多有1件一等品 D、都不是一等品

查看试题解析
8. 袋子中有四个小球，分别写有“美、丽、中、国”四个字，有放回地从中任取一个小球，直到“中”“国”两个字都取到就停止，用随机模拟的方法估计恰好在第三次停止的概率．利用电脑随机产生0到3之间取整数值的随机数，分别用0，1，2，3代表“中、国、美、丽”这四个字，以每三个随机数为一组，表示取球三次的结果，经随机模拟产生了以下18组随机数：
232 321 230 023 123 021 132 220 001

231 130 133 231 031 320 122 103 233

由此可以估计，恰好第三次就停止的概率为（）

A、 $\frac{1}{9}$ B、 $\frac{3}{18}$ C、 $\frac{2}{9}$ D、 $\frac{5}{18}$

查看试题解析
9. 两位男同学和两位女同学随机排成一列，则两位女同学相邻的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
10. 随机掷两枚质地均匀的骰子，它们向上的点数之和不大于6的概率记为 $p_{1}$ ，点数之和大于6的概率记为 $p_{2}$ ，点数之和为奇数的概率记为 $p_{3}$ ，则（）

A、 $p_{1} < p_{2} < p_{3}$ B、 $p_{1} < p_{3} < p_{2}$ C、 $p_{2} < p_{1} < p_{3}$ D、 $p_{3} < p_{1} < p_{2}$

查看试题解析

二、填空题

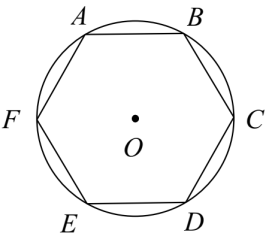
11. 从2名男生和2名女生中任意选择两人在星期六、星期日参加某公益活动，每天一人，则星期六安排一名男生、星期日安排一名女生的概率为．

查看试题解析
12. 从2，3，8，9中任取两个不同的数字，分别记为a，b，则log_ab为整数的概率是．

查看试题解析
13. 掷两次骰子将所得的点数相加，则其和为6的概率为．

查看试题解析
14. 如图， $⊙ O$ 的半径为1六边形 $A B C D E F$ 是 $⊙ O$ 的内接正六边形，从 $A$ ， $B$ ， $C$ ， $D$ ， $E$ ， $F$ 六点中任意取两点，并连接成线段，则线段的长为 $\sqrt{3}$ 的概率是．

查看试题解析

三、解答题（共4题）

15. 有3个完全相同的小球 $a$ ， $b$ ， $c$ ，随机放入甲、乙两个盒子中，求两个盒子都不空的概率．

查看试题解析
16. 有编号为   $A_{1}$ ， $A_{2}$ ， $⋯$ ， $A_{10}$   的10个零件，测量其直径（单位： $c m$ ），得到下面数据： $\begin{array}{l} 编号 & A_{1} & A_{2} & A_{3} & A_{4} & A_{5} & A_{6} & A_{7} & A_{8} & A_{9} & A_{10} \\ 直径 & 1.51 & 1.49 & 1.49 & 1.51 & 1.49 & 1.51 & 1.47 & 1.46 & 1.53 & 1.47 \end{array}$
其中直径在区间   $[1.48 ， 1.52]$   内的零件为一等品．

(1)、从上述10个零件中，随机抽取一个，求这个零件为一等品的概率；

(2)、从一等品零件中，随机抽取2个．
  ① 用零件的编号列出所有可能的抽取结果；
  ② 求这2个零件直径相等的概率．

查看试题解析
17. 某公司为了解所经销商品的使用情况，随机问卷50名使用者，然后根据这50名的问卷评分数据，统计得到如图所示的频率布直方图，其统计数据分组区间为 $[40 ， 50)$ ， $[50 ， 60)$ ， $[60 ， 70)$ ， $[70 ， 80)$ ， $[80 ， 90)$ ， $[90 ， 100]$ ．

(1)、求频率分布直方图中 $a$ 的值；

(2)、求这50名问卷评分数据的中位数；

(3)、从评分在 $[40 ， 60)$ 的问卷者中，随机抽取2人，求此2人评分都在 $[50 ， 60)$ 的概率．

查看试题解析
18. 某校为了解高一学生周末的“阅读时间”，从高一年级中随机调查了100名学生进行调查，获得了每人的周末“阅读时间”（单位：小时），按照 $[0 ， 0.5)$ ， $[0.5 ， 1)$ ， $⋯$ ， $[4 ， 4.5]$ 分成9组，制成样本的频率分布直方图如图所示．

(1)、求图中 $a$ 的值；

(2)、估计该校高一学生周末“阅读时间”的中位数；

(3)、在 $[1 ， 1.5)$ ， $[1.5 ， 2)$ 这两组中采用分层抽样抽取7人，再从7人中随机抽取2人，求抽取的两人恰好都在一组的概率．

查看试题解析