人教A版(2019)必修二8.6空间直线、平面的垂直
试卷更新日期:2023-06-30 类型:单元试卷
一、选择题
-
1. 如图PA垂直于矩形ABCD所在的平面,则图中互相垂直的平面有( )
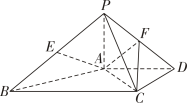
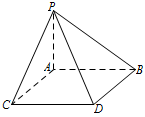 A、2对 B、3对 C、4对 D、5对2. “直线 与平面 内的无数条直线垂直”是“直线 与平面 垂直”的( )A、充分条件 B、必要条件 C、充要条件 D、既非充分条件又非必要条件3. 如图所示,在四面体 中,若 , , 是 的中点,则下列结论中正确的是( )
A、2对 B、3对 C、4对 D、5对2. “直线 与平面 内的无数条直线垂直”是“直线 与平面 垂直”的( )A、充分条件 B、必要条件 C、充要条件 D、既非充分条件又非必要条件3. 如图所示,在四面体 中,若 , , 是 的中点,则下列结论中正确的是( )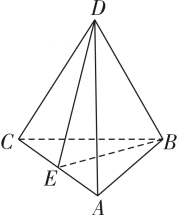 A、 B、 C、 ,且 D、 ,且4. 已知三条直线 , , 和三个平面 , , ,有如下 4 个命题:
A、 B、 C、 ,且 D、 ,且4. 已知三条直线 , , 和三个平面 , , ,有如下 4 个命题:① , ;
② , ;
③ , ;
④ , .
其中正确的两个命题为是( )
A、①② B、③④ C、①④ D、②③5. 若 , 是两个不同的平面, , 是两条不同的直线,且 , ( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则6. 设 , 是两条不同的直线, , 是两个不同的平面,则下列命题正确的是( )A、若 , ,则 B、若 , , ,则 C、若 , , ,则 D、若 , , ,则7. 已知长方体 中,在平面 内任取一点 ,作 于 ,则( )A、 B、 C、 D、以上都有可能8. 如图,正方体 的棱长为1,线段 上有两个动点 , ,且 ,则下列结论中错误的是( )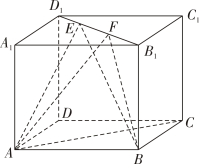 A、 B、 C、三棱锥 的体积为定值 D、 与 的面积相等9. 在正方体 中,点 , 分别在 , 上,且 , ,则下列结论:
A、 B、 C、三棱锥 的体积为定值 D、 与 的面积相等9. 在正方体 中,点 , 分别在 , 上,且 , ,则下列结论:① ;② ;③ ;④ .正确命题的个数是( )
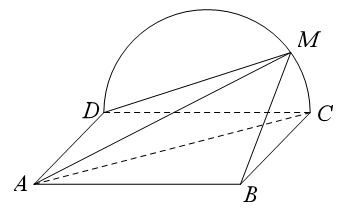
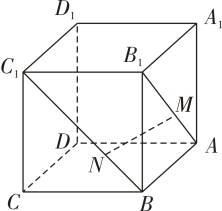 A、4 B、3 C、2 D、110. 如图,在正方形 中, , 分别是 , 的中点, 是 的中点.现在沿 , 及 把这个正方形折成一个空间图形,使 , , 三点重合,重合后的点记为 .那么,在这个空间图形中必有( )
A、4 B、3 C、2 D、110. 如图,在正方形 中, , 分别是 , 的中点, 是 的中点.现在沿 , 及 把这个正方形折成一个空间图形,使 , , 三点重合,重合后的点记为 .那么,在这个空间图形中必有( )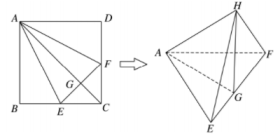 A、 B、 C、 D、11. 如图,在正方形 中, , 分别为 , 的中点, 是 的中点.现沿 , , 把这个正方形折成一个几何体,使 , , 三点重合于点 ,则下列结论中成立的是( )
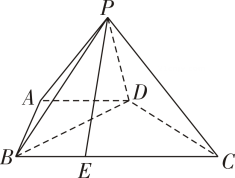
A、 B、 C、 D、11. 如图,在正方形 中, , 分别为 , 的中点, 是 的中点.现沿 , , 把这个正方形折成一个几何体,使 , , 三点重合于点 ,则下列结论中成立的是( )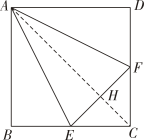 A、 B、 C、 D、12. 在所有棱长都相等的三棱锥 中, , , 分别是 , , 的中点,下列四个命题:
A、 B、 C、 D、12. 在所有棱长都相等的三棱锥 中, , , 分别是 , , 的中点,下列四个命题:( ) ;
( ) ;
( ) ;
( ) .
其中正确命题的序号为( )
A、(2)(3) B、(1)(3) C、(2)(4) D、(1)(4)13. 已知 , 是平面 外的两条不同直线.给出下列三个论断:① ;
② ;
③ .
以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题: .
14. 如图,空间四边形 的对角线 , , , 分别为 , 的中点,并且异面直线 与 所成的角为 ,则 .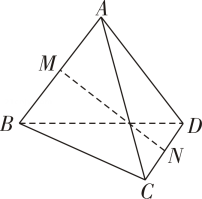 15. 如图,在三棱锥 中, , , 分别是 , , 的中点, ,则 与 所成角的度数为 .
15. 如图,在三棱锥 中, , , 分别是 , , 的中点, ,则 与 所成角的度数为 .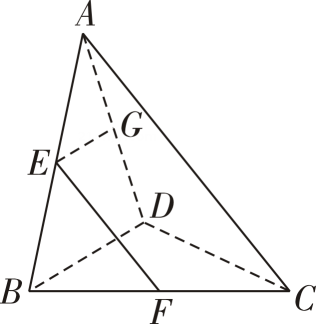 16. 在三棱柱 中, , .若 , ,则异面直线 与 所成的角为 .
16. 在三棱柱 中, , .若 , ,则异面直线 与 所成的角为 .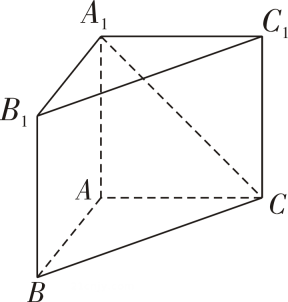 17. 如图, 中, , 是边长为 的 若 , 分别是 , 的中点.
17. 如图, 中, , 是边长为 的 若 , 分别是 , 的中点.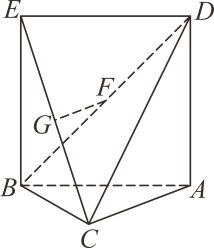 (1)、求证: ;(2)、求证: ;(3)、求 和面 所成角的大小.
(1)、求证: ;(2)、求证: ;(3)、求 和面 所成角的大小.