安徽省安庆潜山市2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-06-30 类型：期末考试

进入出卷网下载

一、单选题

1. 在 $- 2$ ， $- 1$ ， 0，4这四个数中，最小的数是（）

A、 $- 2$ B、 $- 1$ C、0 D、4

查看试题解析
2. 作为世界文化遗产的长城，其总长大约是6700000m，将6700000用科学记数法表示为（）

A、 $6.7 × 1 0^{5}$ B、 $6.7 × 1 0^{6}$ C、 $0.67 \times 1 0^{7}$ D、 $67 \times 1 0^{8}$

查看试题解析
3. 在 $\frac{1}{2}$ ， $π$ ， 4， $2 \frac{1}{3}$ ， 0， $- 0.3$ 中，表示有理数的有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
4. 要反映某市某一周每天的最高气温的变化趋势，宜采用（）

A、条形统计图 B、扇形统计图 C、折线统计图 D、以上均可

查看试题解析
5. “圣诞节”前夕，某超市用3360元购进A，B两种不同型号的圣诞老人玩偶共120套，其中A种型号每套24元，B种号型每套36元．若购买A种型号 $x$ 套，B种型号 $y$ 套，依题意列方程组，正确的是（）

A、 ${\begin{array}{l} x + y = 120 \\ 36 x + 24 y = 3360 \end{array}$ B、 ${\begin{array}{l} x + y = 120 \\ 24 x + 36 y = 3360 \end{array}$ C、 ${\begin{array}{l} 36 x + 24 y = 12 \\ x + y = 3360 \end{array}$ D、 ${\begin{array}{l} 24 x + 36 y = 12 \\ x + y = 3360 \end{array}$

查看试题解析
6. 下列各组的两个数中，运算结果相等的是（）

A、 $2^{3}$ 和 $3^{2}$ B、 $- 3^{3}$ 和 ${(- 3)}^{3}$ C、 $- 2^{2}$ 和 ${(- 2)}^{2}$ D、－|－2|和|－2|

查看试题解析
7. 若单项式 $a^{m - 1} b^{2}$ 与 $\frac{1}{2} a^{2} b^{n}$ 的和仍是单项式，则 $n^{m}$ 的值是（）

A、6 B、4 C、9 D、8

查看试题解析
8. 已知 $∠ α$ 是锐角， $∠ α$ 与 $∠ β$ 互补， $∠ α$ 与 $∠ γ$ 互余，则 $∠ β - ∠ γ$ 的度数为（）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $90 °$

查看试题解析
9. 线段 $A B = 3 c m$ ，点 $C$ 在线段 $A B$ 所在的直线上，且 $B C = 1 c m$ ，则线段 $A C$ 的长度为（）

A、 $4 c m$ B、 $2 c m$ C、 $2 c m$ 或 $4 c m$ D、 $1 c m$ 或 $3 c m$

查看试题解析
10. 已知 $m$ 为正整数，且二元一次方程组 ${\begin{array}{l} m x + 2 y = 10 \\ 3 x - 2 y = 0 \end{array}$ 有整数解，则 $m^{2}$ 的值为（）

A、4 B、64 C、4或64 D、1或64

查看试题解析

二、填空题

11. 观察下列单项式： $- x$ ， $2 x^{2}$ ， $- 3 x^{3}$ ， $4 x^{4}$ ， …，根据你发现的规律，第10个单项式为．

查看试题解析
12. 已知 $| a | = 2 ， | b | = 3 ， | c | = 4 ，$ 且 $a > b > c ，$ 则 $a - b + c =$ .

查看试题解析
13. 将一张纸按如图所示折叠后压平，点 $F$ 在线段 $B C$ 上， $E F$ 、 $G F$ 为两条折痕．若 $∠ 1 = 55 °$ ， $∠ 2 = 24 °$ ， $∠ 3$ 的度数为．

查看试题解析
14. 按如图所示的程序计算，若开始输入的 $x$ 的值为36，则第一次得到的结果为18，第2次得到的结果为9，…．请你探索第2023次得到的结果为．

查看试题解析

三、解答题

15. 计算： $- 1^{6} - (0.5 - \frac{1}{3}) \div \frac{1}{6} \times [- 2 - {(- 3)}^{3}] - | 2^{3} - 3^{2} |$ ．

查看试题解析
16. 解方程： $\frac{1}{3} [x - \frac{1}{2} (x - 1)] = \frac{5}{6} (x - 1)$ ．

查看试题解析
17. 已知： $A + 2 B = 3 a^{2} - a b + 1$ ， $B = a^{2} - 2 a b - 4$ ，若 $| a + 1 | + {(b - 2)}^{2} = 0$ ，计算 $A$ 的值．

查看试题解析
18. 如果关于 $x 、 y$ 的二元一次方程组 ${\begin{array}{l} 3 x - a y = 16 \\ 2 x + b y = 15 \end{array}$ 的解是 ${\begin{array}{l} x = 7 \\ y = 1 \end{array}$ ，那么关于 $x 、 y$ 的二元一次方程组 ${\begin{array}{l} 3 (x + y) - a (x - y) = 16 \\ 2 (x + y) + b (x - y) = 15 \end{array}$ 的解是什么？

查看试题解析
19. 已知：线段 $a$ ， $b$ ， $∠ α$ ， $∠ β$ ．

求作：（要求：仅用无刻度的直尺和圆规作图，不写作法，保留作图痕迹）

(1)、线段 $A B = a + b$ ；

(2)、 $∠ M O N = ∠ α + ∠ β$ ．

查看试题解析
20. 《九章算术》中记载这样一道问题．
原文：“今有五雀六燕，集称之衡，雀俱重，燕俱轻．一雀一燕交而处，衡适平．并燕、雀重一斤．问燕、雀各重几何？”
译文：“今有5只雀、6只燕，分别聚集而且用衡器称之，聚在一起的雀重，燕轻．将1只雀、1只燕交换位置而放，重量相等.5只雀、6只燕的总重量为1斤，问雀、燕每只各重多少斤？”
请解答上述问题．

查看试题解析
21. 某校数学实践小组就近期人们比较关注的五个话题：“A：春运；B：日用商品价格；C：新冠疫情；D：直播带货；E：寒潮天气”，对某小区居民进行了随机抽样调查，每人只能从中选择一个本人最关注的话题，根据调查结果绘制了如图所示的两幅不完整的统计图．
请结合统计图中的信息，解决下列问题：

(1)、数学实践小组在这次活动中，调查的居民共有人；

(2)、将上面的最关注话题条形统计图补充完整；

(3)、最关注话题扇形统计图中的 $a =$ ，话题 $D$ 所在扇形的圆心角是度；

(4)、假设这个小区居民共有9000人，请估计该小区居民中最关注的话题是“日用商品价格”的人数是多少．

查看试题解析
22. 已知数轴上点A表示的数为6，B是数轴上在原点左侧的一点，且A，B两点间的距离为10。动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t $(t > 0)$ 秒。

(1)、数轴上点B表示的数是；当点P运动到AB的中点时，它所表示的数是。

(2)、动点Q从点B出发，以每秒2个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，求：
①当点P运动多少秒时，点P追上点Q？
②当点P运动多少秒时，点P与点Q间的距离为8个单位长度？

查看试题解析
23. 已知将一副三角板（直角三角板OAB和直角三角板OCD，∠AOB=90°，∠ABO=45°，∠CDO=90°，∠COD=60°）

(1)、如图1摆放，点O、A、C在一直线上，则∠BOD的度数是多少？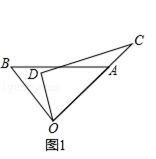

(2)、如图2，将直角三角板OCD绕点O逆时针方向转动，若要OB恰好平分∠COD，则∠AOC的度数是多少？

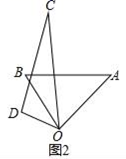(3)、如图3，当三角板OCD摆放在∠AOB内部时，作射线OM平分∠AOC，射线ON平分∠BOD，如果三角板OCD在∠AOB内绕点O任意转动，∠MON的度数是否发生变化？如果不变，求其值；如果变化，说明理由．

查看试题解析