四川省广元市2023年中考数学试卷
试卷更新日期:2023-06-30 类型:中考真卷
一、单选题
-
1. 的相反数是( )A、 B、2 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 某几何体是由四个大小相同的小立方块拼成,其俯视图如图所示,图中数字表示该位置上的小立方块个数,则这个几何体的左视图是( )
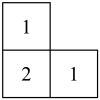 A、
A、 B、
B、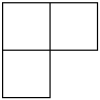 C、
C、 D、
D、 4. 某中学开展“读书节活动”,该中学某语文老师随机抽样调查了本班10名学生平均每周的课外阅读时间,统计如表:
4. 某中学开展“读书节活动”,该中学某语文老师随机抽样调查了本班10名学生平均每周的课外阅读时间,统计如表:每周课外阅读时间(小时)
学生数(人)
下列说法错误的是( )
A、众数是 B、平均数是 C、样本容量是 D、中位数是5. 关于x的一元二次方程根的情况,下列说法中正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定6. 如图,是的直径,点C,D在上,连接 , 若 , 则的度数是( ) A、 B、 C、 D、7. 如图,半径为的扇形中, , 是上一点, , , 垂足分别为 , , 若 , 则图中阴影部分面积为( )
A、 B、 C、 D、7. 如图,半径为的扇形中, , 是上一点, , , 垂足分别为 , , 若 , 则图中阴影部分面积为( )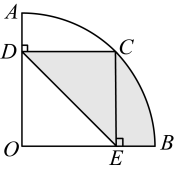 A、 B、 C、 D、8. 向高为10的容器(形状如图)中注水,注满为止,则水深y与注水量x的函数关系的大致图象是( )
A、 B、 C、 D、8. 向高为10的容器(形状如图)中注水,注满为止,则水深y与注水量x的函数关系的大致图象是( )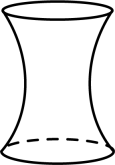 A、
A、 B、
B、 C、
C、 D、
D、 9. 近年来,我市大力发展交通,建成多条快速通道,小张开车从家到单位有两条路线可选择,路线a为全程10千米的普通道路,路线b包含快速通道,全程7千米,走路线b比路线a平均速度提高 , 时间节省10分钟,求走路线a和路线b的平均速度分别是多少?设走路线a的平均速度为x千米/小时,依题意,可列方程为( )A、 B、 C、 D、10. 已知抛物线( , , 是常数且)过和两点,且 , 下列四个结论:;;若抛物线过点 , 则;关于的方程有实数根,则其中正确的结论有( )A、1个 B、2个 C、3个 D、4个
9. 近年来,我市大力发展交通,建成多条快速通道,小张开车从家到单位有两条路线可选择,路线a为全程10千米的普通道路,路线b包含快速通道,全程7千米,走路线b比路线a平均速度提高 , 时间节省10分钟,求走路线a和路线b的平均速度分别是多少?设走路线a的平均速度为x千米/小时,依题意,可列方程为( )A、 B、 C、 D、10. 已知抛物线( , , 是常数且)过和两点,且 , 下列四个结论:;;若抛物线过点 , 则;关于的方程有实数根,则其中正确的结论有( )A、1个 B、2个 C、3个 D、4个二、填空题
-
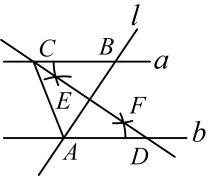
11. 若有意义,则实数x的取值范围是12. 广元市聚焦“1345”发展战略和“十四五”规划,牢牢牵住重点项目建设“牛鼻子”,《2023年广元市重点项目名单》共编列项目300个,其中生态环保项目10个,计划总投资约45亿元,将45亿这个数据用科学记数法表示为 .13. 如图, , 直线l与直线a,b分别交于B,A两点,分别以点A,B为圆心,大于的长为半径画弧,两弧相交于点E,F,作直线 , 分别交直线a,b于点C,D,连接AC,若 , 则的度数为 .
 14. 在我国南宋数学家杨辉所著的《详解九章算术》(1261年)一书中,用如图的三角形解释二项和的乘方规律,因此我们称这个三角形为“杨辉三角”,根据规律第八行从左到右第三个数为 .
14. 在我国南宋数学家杨辉所著的《详解九章算术》(1261年)一书中,用如图的三角形解释二项和的乘方规律,因此我们称这个三角形为“杨辉三角”,根据规律第八行从左到右第三个数为 . 15. 如图,在平面直角坐标系中,已知点 , 点 , 点在轴上,且点在点右方,连接 , , 若 , 则点的坐标为 .
15. 如图,在平面直角坐标系中,已知点 , 点 , 点在轴上,且点在点右方,连接 , , 若 , 则点的坐标为 . 16. 如图, , 半径为2的与角的两边相切,点P是⊙O上任意一点,过点P向角的两边作垂线,垂足分别为E,F,设 , 则t的取值范围是 .
16. 如图, , 半径为2的与角的两边相切,点P是⊙O上任意一点,过点P向角的两边作垂线,垂足分别为E,F,设 , 则t的取值范围是 .
三、解答题
-
17. 计算: .18. 先化简,再求值: , 其中 , .19. 如图,将边长为4的等边三角形纸片沿边上的高剪成两个三角形,用这两个三角形拼成一个平行四边形.
 (1)、画出这个平行四边形(画出一种情况即可);(2)、根据(1)中所画平行四边形求出两条对角线长.20. 为进一步落实“德、智、体、美、劳”五育并举工作,某校开展以“文化、科技、体育、艺术、劳动”为主题的活动,其中体育活动有“一分钟跳绳”比赛项目,为了解学生“一分钟跳绳”的能力,体育老师随机抽取部分学生进行测试并将测试成绩作为样本,绘制出如图所示的频数分布直方图(从左到右依次为第一到第六小组,每小组含最小值,不含最大值)和扇形统计图,请根据统计图中提供的信息解答下列问题:
(1)、画出这个平行四边形(画出一种情况即可);(2)、根据(1)中所画平行四边形求出两条对角线长.20. 为进一步落实“德、智、体、美、劳”五育并举工作,某校开展以“文化、科技、体育、艺术、劳动”为主题的活动,其中体育活动有“一分钟跳绳”比赛项目,为了解学生“一分钟跳绳”的能力,体育老师随机抽取部分学生进行测试并将测试成绩作为样本,绘制出如图所示的频数分布直方图(从左到右依次为第一到第六小组,每小组含最小值,不含最大值)和扇形统计图,请根据统计图中提供的信息解答下列问题: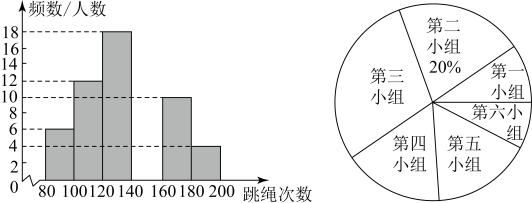 (1)、求第四小组的频数,并补全频数分布直方图;(2)、若“一分钟跳绳”不低于160次的成绩为优秀,本校学生共有1260人,请估计该校学生“一分钟跳绳”成绩为优秀的人数;(3)、若“一分钟跳绳”不低于180次的成绩为满分,经测试某班恰有3名男生1名女生成绩为满分,现要从这4人中随机抽取2人去参加学校组织的“一分钟跳绳”比赛,请用画树状图或列表的方法,求所选2人都是男生的概率.21. “一缕清风银叶转”,某市20台风机依次矗立在云遮雾绕的山脊之上,风叶转动,风能就能转换成电能,造福千家万户.某中学初三数学兴趣小组,为测量风叶的长度进行了实地测量.如图,三片风叶两两所成的角为 , 当其中一片风叶与塔干叠合时,在与塔底D水平距离为60米的E处,测得塔顶部O的仰角 , 风叶的视角 .
(1)、求第四小组的频数,并补全频数分布直方图;(2)、若“一分钟跳绳”不低于160次的成绩为优秀,本校学生共有1260人,请估计该校学生“一分钟跳绳”成绩为优秀的人数;(3)、若“一分钟跳绳”不低于180次的成绩为满分,经测试某班恰有3名男生1名女生成绩为满分,现要从这4人中随机抽取2人去参加学校组织的“一分钟跳绳”比赛,请用画树状图或列表的方法,求所选2人都是男生的概率.21. “一缕清风银叶转”,某市20台风机依次矗立在云遮雾绕的山脊之上,风叶转动,风能就能转换成电能,造福千家万户.某中学初三数学兴趣小组,为测量风叶的长度进行了实地测量.如图,三片风叶两两所成的角为 , 当其中一片风叶与塔干叠合时,在与塔底D水平距离为60米的E处,测得塔顶部O的仰角 , 风叶的视角 .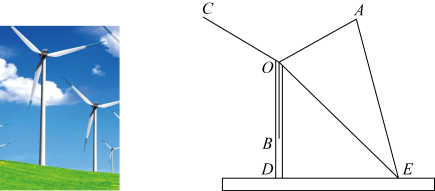 (1)、已知α,β两角和的余弦公式为: , 请利用公式计算;(2)、求风叶的长度.22. 某移动公司推出A,B两种电话计费方式.
(1)、已知α,β两角和的余弦公式为: , 请利用公式计算;(2)、求风叶的长度.22. 某移动公司推出A,B两种电话计费方式.计费方式
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
A
免费
B
免费
(1)、设一个月内用移动电话主叫时间为tmin,根据上表,分别写出在不同时间范围内,方式A,方式B的计费金额关于t的函数解析式;(2)、若你预计每月主叫时间为350min,你将选择A,B哪种计费方式,并说明理由;(3)、请你根据月主叫时间t的不同范围,直接写出最省钱的计费方式.23. 如图,已知一次函数的图象与反比例函数的图象交于 , B两点,与x轴交于点C,将直线沿y轴向上平移3个单位长度后与反比例函数图象交于点D,E. (1)、求k,m的值及C点坐标;(2)、连接 , , 求的面积.24. 如图,为的直径,C为上一点,连接 , 过点C作的切线交延长线于点D,于点E,交于点F.
(1)、求k,m的值及C点坐标;(2)、连接 , , 求的面积.24. 如图,为的直径,C为上一点,连接 , 过点C作的切线交延长线于点D,于点E,交于点F.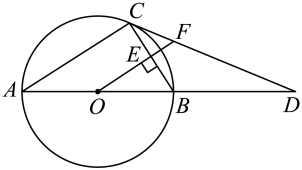 (1)、求证:;(2)、若 , , 求的长.25. 如图1,已知线段 , , 线段绕点在直线上方旋转,连接 , 以为边在上方作 , 且 .
(1)、求证:;(2)、若 , , 求的长.25. 如图1,已知线段 , , 线段绕点在直线上方旋转,连接 , 以为边在上方作 , 且 . (1)、若 , 以为边在上方作 , 且 , , 连接 , 用等式表示线段与的数量关系是 ;(2)、如图2,在(1)的条件下,若 , , , 求的长;(3)、如图3,若 , , , 当的值最大时,求此时的值.26. 如图1,在平面直角坐标系中,已知二次函数的图象与x轴交于点 , , 与轴交于点 .
(1)、若 , 以为边在上方作 , 且 , , 连接 , 用等式表示线段与的数量关系是 ;(2)、如图2,在(1)的条件下,若 , , , 求的长;(3)、如图3,若 , , , 当的值最大时,求此时的值.26. 如图1,在平面直角坐标系中,已知二次函数的图象与x轴交于点 , , 与轴交于点 .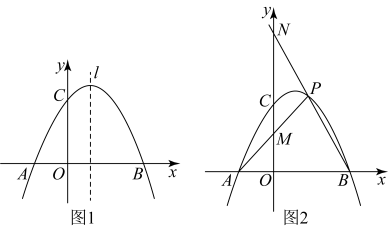 (1)、求抛物线的解析式;(2)、已知为抛物线上一点,为抛物线对称轴上一点,以 , , 为顶点的三角形是等腰直角三角形,且 , 求出点的坐标;(3)、如图 , 为第一象限内抛物线上一点,连接交轴于点 , 连接并延长交轴于点 , 在点运动过程中,是否为定值?若是,求出这个定值;若不是,请说明理由.
(1)、求抛物线的解析式;(2)、已知为抛物线上一点,为抛物线对称轴上一点,以 , , 为顶点的三角形是等腰直角三角形,且 , 求出点的坐标;(3)、如图 , 为第一象限内抛物线上一点,连接交轴于点 , 连接并延长交轴于点 , 在点运动过程中,是否为定值?若是,求出这个定值;若不是,请说明理由.