山西省2023年中考数学试卷
试卷更新日期:2023-06-30 类型:中考真卷
一、单选题
-
1. 计算的结果为( ).A、3 B、 C、 D、2. 全民阅读有助于提升一个国家、一个民族的精神力量.图书馆是开展全民阅读的重要场所.以下是我省四个地市的图书馆标志,其文字上方的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 山西是全国电力外送基地,2022年山西省全年外送电量达到1464亿千瓦时,同比增长 . 数据1464亿千瓦时用科学记数法表示为( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 山西是全国电力外送基地,2022年山西省全年外送电量达到1464亿千瓦时,同比增长 . 数据1464亿千瓦时用科学记数法表示为( ) A、千瓦时 B、千瓦时 C、千瓦时 D、千瓦时5. 如图,四边形内接于为对角线,经过圆心 . 若 , 则的度数为( )
A、千瓦时 B、千瓦时 C、千瓦时 D、千瓦时5. 如图,四边形内接于为对角线,经过圆心 . 若 , 则的度数为( )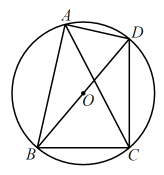 A、 B、 C、 D、6. 一种弹簧秤最大能称不超过的物体,不挂物体时弹簧的长为 , 每挂重物体,弹簧伸长 . 在弹性限度内,挂重后弹簧的长度与所挂物体的质量之间的函数关系式为( )
A、 B、 C、 D、6. 一种弹簧秤最大能称不超过的物体,不挂物体时弹簧的长为 , 每挂重物体,弹簧伸长 . 在弹性限度内,挂重后弹簧的长度与所挂物体的质量之间的函数关系式为( )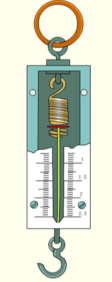 A、 B、 C、 D、7. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心的光线相交于点 , 点为焦点.若 , 则的度数为( )
A、 B、 C、 D、7. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心的光线相交于点 , 点为焦点.若 , 则的度数为( )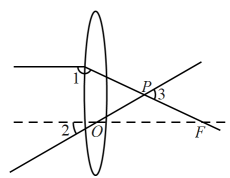 A、 B、 C、 D、8. 已知都在反比例函数的图象上,则a、b、c的关系是( )A、 B、 C、 D、9. 中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为 , 曲线终点为 , 过点的两条切线相交于点 , 列车在从到行驶的过程中转角为 . 若圆曲线的半径 , 则这段圆曲线的长为( ).
A、 B、 C、 D、8. 已知都在反比例函数的图象上,则a、b、c的关系是( )A、 B、 C、 D、9. 中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为 , 曲线终点为 , 过点的两条切线相交于点 , 列车在从到行驶的过程中转角为 . 若圆曲线的半径 , 则这段圆曲线的长为( ).
 A、 B、 C、 D、10. 蜂巢结构精巧,其巢房横截面的形状均为正六边形.如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点均为正六边形的顶点.若点的坐标分别为 , 则点的坐标为( )
A、 B、 C、 D、10. 蜂巢结构精巧,其巢房横截面的形状均为正六边形.如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点均为正六边形的顶点.若点的坐标分别为 , 则点的坐标为( )
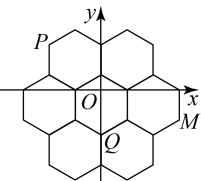 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算(+)(﹣)的结果为 .
12. 如图是一组有规律的图案,它由若干个大小相同的圆片组成.第1个图案中有4个白色圆片,第2个图案中有6个白色圆片,第3个图案中有8个白色圆片,第4个图案中有10个白色圆片,…依此规律,第n个图案中有个白色圆片(用含n的代数式表示) 13. 如图,在中, . 以点为圆心,以的长为半径作弧交边于点 , 连接 . 分别以点为圆心,以大于的长为半径作弧,两弧交于点 , 作射线交于点 , 交边于点 , 则的值为 .
13. 如图,在中, . 以点为圆心,以的长为半径作弧交边于点 , 连接 . 分别以点为圆心,以大于的长为半径作弧,两弧交于点 , 作射线交于点 , 交边于点 , 则的值为 .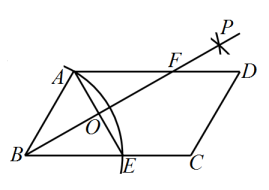 14. 中国古代的“四书”是指《论语》《孟子》《大学》《中庸》,它是儒家思想的核心著作,是中国传统文化的重要组成部分,若从这四部著作中随机抽取两本(先随机抽取一本,不放回,再随机抽取另一本),则抽取的两本恰好是《论语》和《大学》的概率是 .
14. 中国古代的“四书”是指《论语》《孟子》《大学》《中庸》,它是儒家思想的核心著作,是中国传统文化的重要组成部分,若从这四部著作中随机抽取两本(先随机抽取一本,不放回,再随机抽取另一本),则抽取的两本恰好是《论语》和《大学》的概率是 . 15. 如图,在四边形中, , 对角线相交于点 . 若 , 则的长为 .
15. 如图,在四边形中, , 对角线相交于点 . 若 , 则的长为 .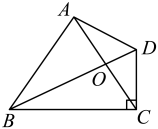
三、解答题
-
16.(1)、计算:;(2)、计算: .17. 解方程: .18. 为增强学生的社会实践能力,促进学生全面发展,某校计划建立小记者站,有20名学生报名参加选拔.报名的学生需参加采访、写作、摄影三项测试,每项测试均由七位评委打分(满分100分),取平均分作为该项的测试成绩,再将采访、写作、摄影三项的测试成绩按的比例计算出每人的总评成绩.

小悦、小涵的三项测试成绩和总评成绩如下表,这20名学生的总评成绩频数直方图(每组含最小值,不含最大值)如下图
选手
测试成绩/分
总评成绩/分
采访
写作
摄影
小悦
83
72
80
78
小涵
86
84
▲
▲
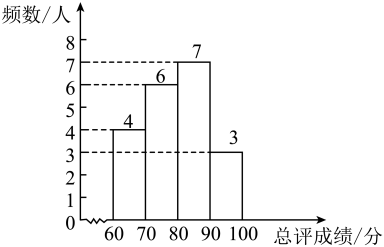 (1)、在摄影测试中,七位评委给小涵打出的分数如下:67,72,68,69,74,69,71.这组数据的中位数是分,众数是分,平均数是分;(2)、请你计算小涵的总评成绩;(3)、学校决定根据总评成绩择优选拔12名小记者.试分析小悦、小涵能否入选,并说明理由.19. 风陵渡黄河公路大桥是连接山西、陕西、河南三省的交通要塞.该大桥限重标志牌显示,载重后总质量超过30吨的车辆禁止通行.现有一辆自重8吨的卡车,要运输若干套某种设备,每套设备由1个A部件和3个B部件组成,这种设备必须成套运输.已知1个A部件和2个B部件的总质量为2.8吨,2个A部件和3个B部件的质量相等.
(1)、在摄影测试中,七位评委给小涵打出的分数如下:67,72,68,69,74,69,71.这组数据的中位数是分,众数是分,平均数是分;(2)、请你计算小涵的总评成绩;(3)、学校决定根据总评成绩择优选拔12名小记者.试分析小悦、小涵能否入选,并说明理由.19. 风陵渡黄河公路大桥是连接山西、陕西、河南三省的交通要塞.该大桥限重标志牌显示,载重后总质量超过30吨的车辆禁止通行.现有一辆自重8吨的卡车,要运输若干套某种设备,每套设备由1个A部件和3个B部件组成,这种设备必须成套运输.已知1个A部件和2个B部件的总质量为2.8吨,2个A部件和3个B部件的质量相等. (1)、求1个A部件和1个B部件的质量各是多少;(2)、卡车一次最多可运输多少套这种设备通过此大桥?20. 2023年3月,水利部印发《母亲河复苏行动河湖名单(2022-2025年)》,我省境内有汾河、桑干河、洋河、清漳河、浊漳河、沁河六条河流入选.在推进实施母亲河复苏行动中,需要砌筑洛种驳岸(也叫护坡).某校“综合与实践”小组的同学把“母亲河驳岸的调研与计算”作为一项课题活动,利用课余时间完成了实践调查,并形成了如下活动报告.请根据活动报告计算和的长度(结果精确到 . 参考数据: , )。
(1)、求1个A部件和1个B部件的质量各是多少;(2)、卡车一次最多可运输多少套这种设备通过此大桥?20. 2023年3月,水利部印发《母亲河复苏行动河湖名单(2022-2025年)》,我省境内有汾河、桑干河、洋河、清漳河、浊漳河、沁河六条河流入选.在推进实施母亲河复苏行动中,需要砌筑洛种驳岸(也叫护坡).某校“综合与实践”小组的同学把“母亲河驳岸的调研与计算”作为一项课题活动,利用课余时间完成了实践调查,并形成了如下活动报告.请根据活动报告计算和的长度(结果精确到 . 参考数据: , )。课题
母亲河驳岸的调研与计算
调查方式
资料查阅、水利部门走访、实地查看了解
功能
驳岸是用来保护河岸,阻止河岸崩塌或冲刷的构筑物
驳岸剖面图


相关数据及说明,图中,点A,B,C,D,E在同一竖直平面内,与均与地面平行,岸墙于点A, , , , ,
计算结果
交流展示
21. 阅读与思考:下面是一位同学的数学学习笔记,请仔细阅读并完成相应任务.瓦里尼翁平行四边形
我们知道,如图1,在四边形中,点分别是边 , 的中点,顺次连接 , 得到的四边形是平行四边形.
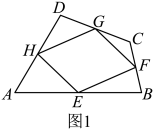
我查阅了许多资料,得知这个平行四边形被称为瓦里尼翁平行四边形.瓦里尼翁是法国数学家、力学家.瓦里尼翁平行四边形与原四边形关系密切.

①当原四边形的对角线满足一定关系时,瓦里尼翁平行四边形可能是菱形、矩形或正方形.
②瓦里尼翁平行四边形的周长与原四边形对角线的长度也有一定关系.
③瓦里尼翁平行四边形的面积等于原四边形面积的一半.此结论可借助图1证明如下:
证明:如图2,连接 , 分别交于点 , 过点作于点 , 交于点 .
∵分别为的中点,∴ . (依据1)
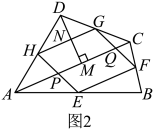
∴ . ∵ , ∴ .
∵四边形是瓦里尼翁平行四边形,∴ , 即 .
∵ , 即 ,
∴四边形是平行四边形.(依据2)∴ .
∵ , ∴ . 同理,…
任务:
(1)、填空:材料中的依据1是指: .依据2是指: .
(2)、请用刻度尺、三角板等工具,画一个四边形及它的瓦里尼翁平行四边形 , 使得四边形为矩形;(要求同时画出四边形的对角线)(3)、在图1中,分别连接得到图3,请猜想瓦里尼翁平行四边形的周长与对角线长度的关系,并证明你的结论.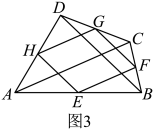 22. 问题情境:“综合与实践”课上,老师提出如下问题:将图1中的矩形纸片沿对角线剪开,得到两个全等的三角形纸片,表示为和 , 其中 . 将和按图2所示方式摆放,其中点与点重合(标记为点).当时,延长交于点 . 试判断四边形的形状,并说明理由.
22. 问题情境:“综合与实践”课上,老师提出如下问题:将图1中的矩形纸片沿对角线剪开,得到两个全等的三角形纸片,表示为和 , 其中 . 将和按图2所示方式摆放,其中点与点重合(标记为点).当时,延长交于点 . 试判断四边形的形状,并说明理由.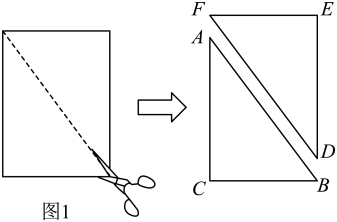 (1)、数学思考:谈你解答老师提出的问题;(2)、深入探究:老师将图2中的绕点逆时针方向旋转,使点落在内部,并让同学们提出新的问题.
(1)、数学思考:谈你解答老师提出的问题;(2)、深入探究:老师将图2中的绕点逆时针方向旋转,使点落在内部,并让同学们提出新的问题.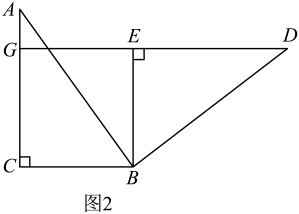
①“善思小组”提出问题:如图3,当时,过点作交的延长线于点与交于点 . 试猜想线段和的数量关系,并加以证明.请你解答此问题;
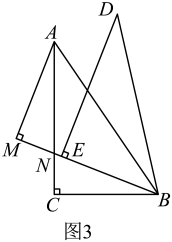
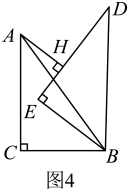
②“智慧小组”提出问题:如图4,当时,过点作于点 , 若 , 求的长.请你思考此问题,直接写出结果.
 23. 如图,二次函数的图象与轴的正半轴交于点A,经过点A的直线与该函数图象交于点 , 与轴交于点C.
23. 如图,二次函数的图象与轴的正半轴交于点A,经过点A的直线与该函数图象交于点 , 与轴交于点C.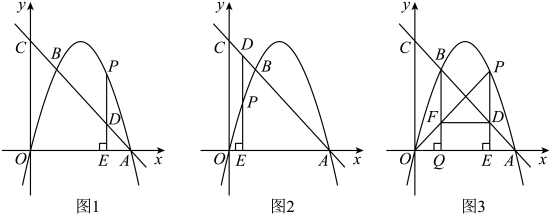 (1)、求直线的函数表达式及点C的坐标;(2)、点是第一象限内二次函数图象上的一个动点,过点作直线轴于点 , 与直线交于点D,设点的横坐标为 .
(1)、求直线的函数表达式及点C的坐标;(2)、点是第一象限内二次函数图象上的一个动点,过点作直线轴于点 , 与直线交于点D,设点的横坐标为 .①当时,求的值;
②当点在直线上方时,连接 , 过点作轴于点 , 与交于点 , 连接 . 设四边形的面积为 , 求关于的函数表达式,并求出S的最大值.