山东省聊城市2023年中考数学试卷
试卷更新日期:2023-06-30 类型:中考真卷
一、单选题
-
1. 的值为( )A、0 B、1 C、 D、2. 如图所示几何体的主视图是( )
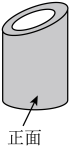 A、
A、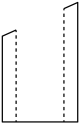 B、
B、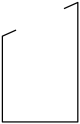 C、
C、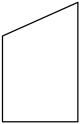 D、
D、 3. 4月15日是全民国家安全教育日.某校为了摸清该校1500名师生的国家安全知识掌握情况,从中随机抽取了150名师生进行问卷调查.这项调查中的样本是( )A、1500名师生的国家安全知识掌握情况 B、150 C、从中抽取的150名师生的国家安全知识掌握情况 D、从中抽取的150名师生4. 若一元二次方程有实数解,则m的取值范围是( )A、 B、 C、且 D、且5. 如图,分别过的顶点A,B作 . 若 , , 则的度数为( )
3. 4月15日是全民国家安全教育日.某校为了摸清该校1500名师生的国家安全知识掌握情况,从中随机抽取了150名师生进行问卷调查.这项调查中的样本是( )A、1500名师生的国家安全知识掌握情况 B、150 C、从中抽取的150名师生的国家安全知识掌握情况 D、从中抽取的150名师生4. 若一元二次方程有实数解,则m的取值范围是( )A、 B、 C、且 D、且5. 如图,分别过的顶点A,B作 . 若 , , 则的度数为( ) A、 B、 C、 D、6. 如图,点O是外接圆的圆心,点I是的内心,连接 , . 若 , 则的度数为( )
A、 B、 C、 D、6. 如图,点O是外接圆的圆心,点I是的内心,连接 , . 若 , 则的度数为( ) A、 B、 C、 D、7. 若关于x的分式方程的解为非负数,则m的取值范围是( )A、且 B、且 C、且 D、且8. 如图,在直角坐标系中,各点坐标分别为 , , . 先作关于x轴成轴对称的 , 再把平移后得到 . 若 , 则点坐标为( )
A、 B、 C、 D、7. 若关于x的分式方程的解为非负数,则m的取值范围是( )A、且 B、且 C、且 D、且8. 如图,在直角坐标系中,各点坐标分别为 , , . 先作关于x轴成轴对称的 , 再把平移后得到 . 若 , 则点坐标为( ) A、 B、 C、 D、9. 如图,该几何体是由一个大圆锥截去上部的小圆锥后剩下的部分.若该几何体上、下两个圆的半径分别为1和2,原大圆锥高的剩余部分为 , 则其侧面展开图的面积为( )
A、 B、 C、 D、9. 如图,该几何体是由一个大圆锥截去上部的小圆锥后剩下的部分.若该几何体上、下两个圆的半径分别为1和2,原大圆锥高的剩余部分为 , 则其侧面展开图的面积为( ) A、 B、 C、 D、10. 甲乙两地相距a千米,小亮8:00乘慢车从甲地去乙地,10分钟后小莹乘快车从乙地赶往甲地.两人分别距甲地的距离y(千米)与两人行驶时刻t(×时×分)的函数图象如图所示,则小亮与小莹相遇的时刻为( )
A、 B、 C、 D、10. 甲乙两地相距a千米,小亮8:00乘慢车从甲地去乙地,10分钟后小莹乘快车从乙地赶往甲地.两人分别距甲地的距离y(千米)与两人行驶时刻t(×时×分)的函数图象如图所示,则小亮与小莹相遇的时刻为( ) A、8:28 B、8:30 C、8:32 D、8:3511. 已知二次函数的部分图象如图所示,图象经过点 , 其对称轴为直线 . 下列结论:①;②若点 , 均在二次函数图象上,则;③关于x的一元二次方程有两个相等的实数根;④满足的x的取值范围为 . 其中正确结论的个数为( ).
A、8:28 B、8:30 C、8:32 D、8:3511. 已知二次函数的部分图象如图所示,图象经过点 , 其对称轴为直线 . 下列结论:①;②若点 , 均在二次函数图象上,则;③关于x的一元二次方程有两个相等的实数根;④满足的x的取值范围为 . 其中正确结论的个数为( ). A、1个 B、2个 C、3个 D、4个12. 如图,已知等腰直角 , , , 点C是矩形与的公共顶点,且 , ;点D是延长线上一点,且 . 连接 , , 在矩形绕点C按顺时针方向旋转一周的过程中,当线段达到最长和最短时,线段对应的长度分别为m和n,则的值为( )
A、1个 B、2个 C、3个 D、4个12. 如图,已知等腰直角 , , , 点C是矩形与的公共顶点,且 , ;点D是延长线上一点,且 . 连接 , , 在矩形绕点C按顺时针方向旋转一周的过程中,当线段达到最长和最短时,线段对应的长度分别为m和n,则的值为( ) A、2 B、3 C、 D、
A、2 B、3 C、 D、二、填空题
-
13. 计算: .14. 若不等式组的解集为 , 则m的取值范围是 .15. 如图,在中,的垂直平分线交于点 , 交于点O,连接 , , 过点C作 , 交的延长线于点F,连接 . 若 , , 则四边形的面积为 .
 .16. 在一个不透明的袋子中,装有五个分别标有数字 , , 0,2,的小球,这些小球除数字外其他完全相同.从袋子中随机摸出两个小球,两球上的数字之积恰好是有理数的概率为 .17. 如图,图中数字是从1开始按箭头方向排列的有序数阵.从3开始,把位于同一列且在拐角处的两个数字提取出来组成有序数对:;;;;…如果单把每个数对中的第一个或第二个数字按顺序排列起来研究,就会发现其中的规律.请写出第n个数对: .
.16. 在一个不透明的袋子中,装有五个分别标有数字 , , 0,2,的小球,这些小球除数字外其他完全相同.从袋子中随机摸出两个小球,两球上的数字之积恰好是有理数的概率为 .17. 如图,图中数字是从1开始按箭头方向排列的有序数阵.从3开始,把位于同一列且在拐角处的两个数字提取出来组成有序数对:;;;;…如果单把每个数对中的第一个或第二个数字按顺序排列起来研究,就会发现其中的规律.请写出第n个数对: .
三、解答题
-
18. 先化简,再求值: , 其中 .19. 如图,在四边形中,点E是边上一点,且 , .
 (1)、求证:;(2)、若 , 时,求的面积.20. 某中学把开展课外经典阅读活动作为一项引领学生明是非、知荣辱、立志向、修言行的德育举措.为了调查活动开展情况,需要了解全校2000名学生一周的课外经典阅读时间.从本校学生中随机抽取100名进行调查,将调查的一周课外经典阅读的平均时间分为5组:①;②;③;④;⑤ , 并将调查结果用如图所示的统计图描述.
(1)、求证:;(2)、若 , 时,求的面积.20. 某中学把开展课外经典阅读活动作为一项引领学生明是非、知荣辱、立志向、修言行的德育举措.为了调查活动开展情况,需要了解全校2000名学生一周的课外经典阅读时间.从本校学生中随机抽取100名进行调查,将调查的一周课外经典阅读的平均时间分为5组:①;②;③;④;⑤ , 并将调查结果用如图所示的统计图描述.
根据以上信息,解答下列问题:
(1)、本次调查中,一周课外经典阅读的平均时间的众数和中位数分别落在第组和第组(填序号);一周课外经典阅读的平均时间达到4小时的学生人数占被调查人数的百分比为;估计全校一周课外经典阅读的平均时间达到4小时的学生有人;(2)、若把各组阅读时间的下限与上限的中间值近似看作该组的平均阅读时间,估计这100名学生一周课外经典阅读的平均时间是多少?(3)、若把一周课外经典阅读的平均时间达到4小时的人数百分比超过 , 作为衡量此次开展活动成功的标准,请你评价此次活动,并提出合理化的建议.21. 今年五一小长假期间,我市迎来了一个短期旅游高峰.某热门景点的门票价格规定见下表:票的种类
A
B
C
购票人数/人
1~50
51~100
100以上
票价/元
50
45
40
某旅行社接待的甲、乙两个旅游团共102人(甲团人数多于乙团),在打算购买门票时,如果把两团联合作为一个团体购票会比两团分别各自购票节省730元.
(1)、求两个旅游团各有多少人?(2)、一个人数不足50人的旅游团,当游客人数最低为多少人时,购买B种门票比购买A种门票节省?22. 东昌湖西岸的明珠大剧院,隔湖与远处的角楼、城门楼、龙堤、南关桥等景观遥相呼应.如图所示,城门楼B在角楼A的正东方向处,南关桥C在城门楼B的正南方向处.在明珠大剧院P测得角楼A在北偏东方向,南关桥C在南偏东方向(点A,B,C,P四点在同一平面内).求明珠大剧院到龙堤的距离(结果精确到).(参考数据: , , , , , )
 23. 如图,一次函数的图像与反比例函数的图像相交于 , 两点.
23. 如图,一次函数的图像与反比例函数的图像相交于 , 两点. (1)、求反比例函数和一次函数的表达式;(2)、点在x轴负半轴上,连接AP,过点B作 , 交的图像于点Q,连接PQ.当时,若四边形APQB的面积为36,求n的值.
(1)、求反比例函数和一次函数的表达式;(2)、点在x轴负半轴上,连接AP,过点B作 , 交的图像于点Q,连接PQ.当时,若四边形APQB的面积为36,求n的值.

