湖南省郴州市2023年中考数学试卷
试卷更新日期:2023-06-30 类型:中考真卷
一、单选题
-
1. 的倒数是( )A、2 B、 C、 D、2. 下列图形中,能由图形通过平移得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 下列几何体中,各自的三视图完全一样的是( )A、
3. 下列运算正确的是( )A、 B、 C、 D、4. 下列几何体中,各自的三视图完全一样的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列问题适合全面调查的是( )A、调查市场上某品牌灯泡的使用寿命 B、了解全市人民对湖南省第二届旅发大会的关注情况 C、了解郴江河的水质情况 D、神舟十六号飞船发射前对飞船仪器设备的检查6. 一元一次不等式组的解集在数轴上表示正确的是( )A、
5. 下列问题适合全面调查的是( )A、调查市场上某品牌灯泡的使用寿命 B、了解全市人民对湖南省第二届旅发大会的关注情况 C、了解郴江河的水质情况 D、神舟十六号飞船发射前对飞船仪器设备的检查6. 一元一次不等式组的解集在数轴上表示正确的是( )A、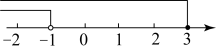 B、
B、 C、
C、 D、
D、 7. 小王从A地开车去B地,两地相距240km.原计划平均速度为km/h,实际平均速度提高了50%,结果提前1小时到达.由此可建立方程为( )A、 B、 C、 D、8. 第11届中国(湖南)矿物宝石国际博览会在我市举行,小方一家上午开车前往会展中心参观.途中汽车发生故障,原地修车花了一段时间.车修好后,他们继续开车赶往会展中心.以下是他们家出发后离家的距离与时间的函数图象.分析图中信息,下列说法正确的是( )
7. 小王从A地开车去B地,两地相距240km.原计划平均速度为km/h,实际平均速度提高了50%,结果提前1小时到达.由此可建立方程为( )A、 B、 C、 D、8. 第11届中国(湖南)矿物宝石国际博览会在我市举行,小方一家上午开车前往会展中心参观.途中汽车发生故障,原地修车花了一段时间.车修好后,他们继续开车赶往会展中心.以下是他们家出发后离家的距离与时间的函数图象.分析图中信息,下列说法正确的是( )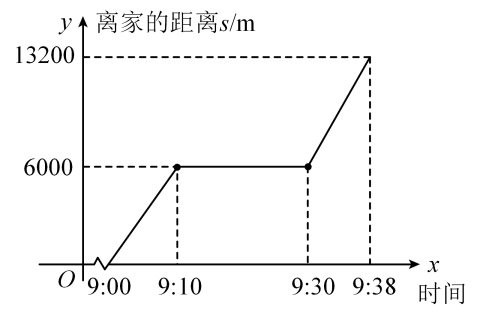 A、途中修车花了 B、修车之前的平均速度是/ C、车修好后的平均速度是/ D、车修好后的平均速度是修车之前的平均速度的倍
A、途中修车花了 B、修车之前的平均速度是/ C、车修好后的平均速度是/ D、车修好后的平均速度是修车之前的平均速度的倍二、填空题
-
9. 计算: .10. 在一次函数中,随的增大而增大,则的值可以是(任写一个符合条件的数即可).11. 在一个不透明的袋子中装有3个白球和7个红球,它们除颜色外,大小、质地都相同.从袋子中随机取出一个球,是红球的概率是 .12. 抛物线与轴只有一个交点,则 .13. 为积极响应“助力旅发大会,唱响美丽郴州”的号召,某校在各年级开展合唱比赛,规定每支参赛队伍的最终成绩按歌曲内容占30%,演唱技巧占50%,精神面貌占20%考评.某参赛队歌曲内容获得90分,演唱技巧获得94分,精神面貌获得95分.则该参赛队的最终成绩是分.14. 在 Rt △ABC中, ∠ACB=90°,AC=6,BC=8,D是AB的中点,则 .15. 如图,某博览会上有一圆形展示区,在其圆形边缘的点处安装了一台监视器,它的监控角度是 , 为了监控整个展区,最少需要在圆形边缘上共安装这样的监视器台.
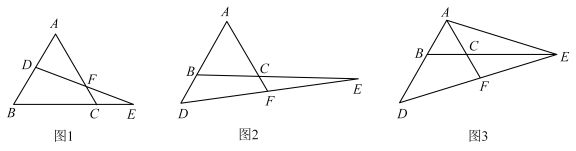
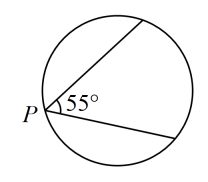 16. 如图,在中, , , . 将绕点逆时针旋转,得到 , 若点的对应点恰好落在线段上,则点的运动路径长是cm(结果用含的式子表示).
16. 如图,在中, , , . 将绕点逆时针旋转,得到 , 若点的对应点恰好落在线段上,则点的运动路径长是cm(结果用含的式子表示).
三、解答题
-
17. 计算: .18. 先化简,再求值: , 其中 .19. 某校计划组织学生外出开展研学活动,在选择研学活动地点时,随机抽取了部分学生进行调查,要求被调查的学生从A、B、C、D、E五个研学活动地点中选择自己最喜欢的一个.根据调查结果,编制了如下两幅不完整的统计图.
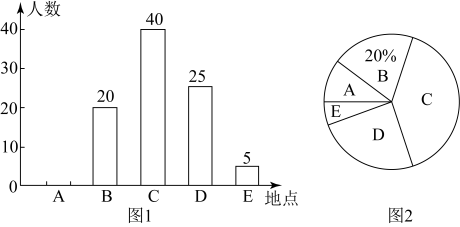 (1)、请把图1中缺失的数据,图形补充完整;(2)、请计算图2中研学活动地点C所在扇形的圆心角的度数;(3)、若该校共有1200名学生,请估计最喜欢去D地研学的学生人数.20. 如图,四边形是平行四边形.
(1)、请把图1中缺失的数据,图形补充完整;(2)、请计算图2中研学活动地点C所在扇形的圆心角的度数;(3)、若该校共有1200名学生,请估计最喜欢去D地研学的学生人数.20. 如图,四边形是平行四边形. (1)、尺规作图;作对角线的垂直平分线(保留作图痕迹);(2)、若直线分别交 , 于 , 两点,求证:四边形是菱形21. 某次军事演习中,一艘船以的速度向正东航行,在出发地测得小岛在它的北偏东方向,小时后到达处,测得小岛在它的北偏西方向,求该船在航行过程中与小岛的最近距离(参考数据: , . 结果精确到).
(1)、尺规作图;作对角线的垂直平分线(保留作图痕迹);(2)、若直线分别交 , 于 , 两点,求证:四边形是菱形21. 某次军事演习中,一艘船以的速度向正东航行,在出发地测得小岛在它的北偏东方向,小时后到达处,测得小岛在它的北偏西方向,求该船在航行过程中与小岛的最近距离(参考数据: , . 结果精确到). 22. 随旅游旺季的到来,某景区游客人数逐月增加,2月份游客人数为1.6万人,4月份游客人数为2.5万人.(1)、求这两个月中该景区游客人数的月平均增长率;(2)、预计5月份该景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率.已知该景区5月1日至5月21日已接待游客2.125万人,则5月份后10天日均接待游客人数最多是多少万人?23. 如图,在中,是直径,点是圆上一点.在的延长线上取一点 , 连接 , 使 .
22. 随旅游旺季的到来,某景区游客人数逐月增加,2月份游客人数为1.6万人,4月份游客人数为2.5万人.(1)、求这两个月中该景区游客人数的月平均增长率;(2)、预计5月份该景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率.已知该景区5月1日至5月21日已接待游客2.125万人,则5月份后10天日均接待游客人数最多是多少万人?23. 如图,在中,是直径,点是圆上一点.在的延长线上取一点 , 连接 , 使 .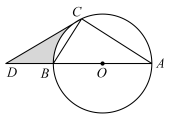 (1)、求证:直线是的切线;(2)、若 , , 求图中阴影部分的面积(结果用含的式子表示).24. 在实验课上,小明做了一个试验.如图,在仪器左边托盘(固定)中放置一个物体,在右边托盘(可左右移动)中放置一个可以装水的容器,容器的质量为 . 在容器中加入一定质量的水,可以使仪器左右平衡.改变托盘与点的距离()(),记录容器中加入的水的质量,得到下表:
(1)、求证:直线是的切线;(2)、若 , , 求图中阴影部分的面积(结果用含的式子表示).24. 在实验课上,小明做了一个试验.如图,在仪器左边托盘(固定)中放置一个物体,在右边托盘(可左右移动)中放置一个可以装水的容器,容器的质量为 . 在容器中加入一定质量的水,可以使仪器左右平衡.改变托盘与点的距离()(),记录容器中加入的水的质量,得到下表:
托盘与点的距离
30
25
20
15
10
容器与水的总质量
10
12
15
20
30
加入的水的质量
5
7
10
15
25
把上表中的与各组对应值作为点的坐标,在平面直角坐标系中描出这些点,并用光滑的曲线连接起来,得到如图所示的关于的函数图象.
 (1)、请在该平面直角坐标系中作出关于的函数图象;(2)、观察函数图象,并结合表中的数据:
(1)、请在该平面直角坐标系中作出关于的函数图象;(2)、观察函数图象,并结合表中的数据:①猜测与之间的函数关系,并求关于的函数表达式;
②求关于的函数表达式;
③当时,随的增大而(填“增大”或“减小”),随的增大而(填“增大”或“减小”),的图象可以由的图象向(以“上”或“下”或“左”或“右”)平移得到.
(3)、若在容器中加入的水的质量(g)满足 , 求托盘与点的距离(cm)的取值范围.