湖南省株洲市2023年中考数学试卷
试卷更新日期:2023-06-30 类型:中考真卷
一、单选题
-
1. 2的相反数是( )A、2 B、-2 C、 D、2. 计算:( )A、 B、 C、 D、3. 计算:( )A、 B、6 C、 D、84. 从6名男生和4名女生的注册学号中随机抽取一个学号,则抽到的学号为男生的概率是( )A、 B、 C、 D、5. 一技术人员用刻度尺(单位:)测量某三角形部件的尺寸.如图所示,已知 , 点D为边的中点,点A、B对应的刻度为1、7,则( )
 A、 B、 C、 D、6. 下列哪个点在反比例函数的图像上?( )A、 B、 C、 D、7. 将关于x的分式方程去分母可得( )A、 B、 C、 D、8. 如图所示,在矩形中, , 与相交于点O,下列说法正确的是( )
A、 B、 C、 D、6. 下列哪个点在反比例函数的图像上?( )A、 B、 C、 D、7. 将关于x的分式方程去分母可得( )A、 B、 C、 D、8. 如图所示,在矩形中, , 与相交于点O,下列说法正确的是( )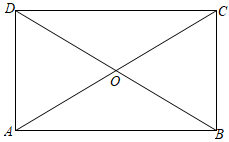 A、点O为矩形的对称中心 B、点O为线段的对称中心 C、直线为矩形的对称轴 D、直线为线段的对称轴9. 如图所示,直线l为二次函数的图像的对称轴,则下列说法正确的是( )
A、点O为矩形的对称中心 B、点O为线段的对称中心 C、直线为矩形的对称轴 D、直线为线段的对称轴9. 如图所示,直线l为二次函数的图像的对称轴,则下列说法正确的是( ) A、b恒大于0 B、a,b同号 C、a,b异号 D、以上说法都不对10. 申报某个项目时,某7个区域提交的申报表数量的前5名的数据统计如图所示,则这7个区域提交该项目的申报表数量的中位数是( )
A、b恒大于0 B、a,b同号 C、a,b异号 D、以上说法都不对10. 申报某个项目时,某7个区域提交的申报表数量的前5名的数据统计如图所示,则这7个区域提交该项目的申报表数量的中位数是( )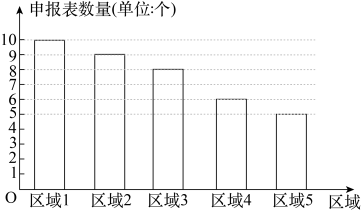 A、8 B、7 C、6 D、5
A、8 B、7 C、6 D、5二、填空题
-
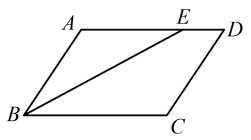
11. 计算: .12. 因式分解 .13. 关于的不等式的解集为 .14. 如图,在平行四边形中, , , 的平分线交于点E,则的长为 .
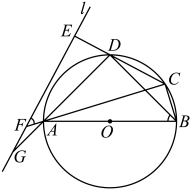
 15. 如图所示,点A、B、C是上不同的三点,点O在的内部,连接、 , 并延长线段交线段于点D.若 , 则度.
15. 如图所示,点A、B、C是上不同的三点,点O在的内部,连接、 , 并延长线段交线段于点D.若 , 则度.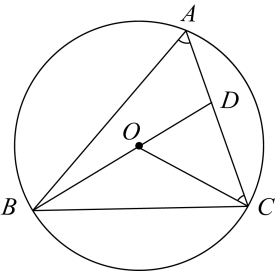 16. 血压包括收缩压和舒张压,分别代表心脏收缩时和舒张时的压力.收缩压的正常范围是: , 舒张压的正常范围是: . 现五人A、B、C、D、E的血压测量值统计如下:
16. 血压包括收缩压和舒张压,分别代表心脏收缩时和舒张时的压力.收缩压的正常范围是: , 舒张压的正常范围是: . 现五人A、B、C、D、E的血压测量值统计如下:
则这五人中收缩压和舒张压均在正常范围内的人有个.
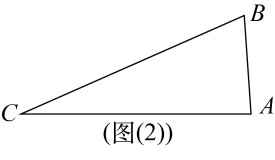
17. 《周礼考工记》中记载有:“……半矩谓之宣(xuān),一宣有半谓之欘(zhú)……”意思是:“……直角的一半的角叫做宣,一宣半的角叫做欘……”.即:1宣矩,1欘宣(其中,1矩),问题:图(1)为中国古代一种强弩图,图(2)为这种强弩图的部分组件的示意图,若矩,欘,则度.

 18. 已知实数m、、满足: .
18. 已知实数m、、满足: .①若 , 则 .
②若m、、为正整数 , 则符合条件的有序实数对有个
三、解答题
-
19. 计算:20. 先化简,再求值: , 其中 .21. 如图所示,在中,点D、E分别为的中点,点H在线段上,连接 , 点G、F分别为的中点.
 (1)、求证:四边形为平行四边形(2)、 , 求线段的长度.22. 某花店每天购进支某种花,然后出售.如果当天售不完,那么剩下的这种花进行作废处理、该花店记录了天该种花的日需求量n(n为正整数,单位:支),统计如下表:
(1)、求证:四边形为平行四边形(2)、 , 求线段的长度.22. 某花店每天购进支某种花,然后出售.如果当天售不完,那么剩下的这种花进行作废处理、该花店记录了天该种花的日需求量n(n为正整数,单位:支),统计如下表:日需求量n
天数
1
1
2
4
1
1
(1)、求该花店在这天中出现该种花作废处理情形的天数;(2)、当时,日利润y(单位:元)关于n的函数表达式为:;当时,日利润为元.①当时,间该花店这天的利润为多少元?
②求该花店这天中日利润为元的日需求量的频率.
23. 如图所示,在某交叉路口,一货车在道路①上点A处等候“绿灯”一辆车从被山峰遮挡的道路②上的点B处由南向北行驶.已知 , , 线段的延长线交直线于点D.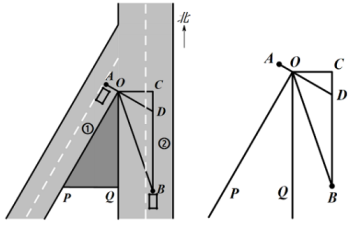 (1)、求的大小;(2)、若在点B处测得点O在北偏西方向上,其中米.问该轿车至少行驶多少米才能发现点A处的货车?(当该轿车行驶至点D处时,正好发现点A处的货车)24. 如图所示,在平面直角坐标系中,四边形为正方形,其中点A、C分别在x轴负半轴,y轴负半轴上,点B在第三象限内,点 , 点在函数的图像上
(1)、求的大小;(2)、若在点B处测得点O在北偏西方向上,其中米.问该轿车至少行驶多少米才能发现点A处的货车?(当该轿车行驶至点D处时,正好发现点A处的货车)24. 如图所示,在平面直角坐标系中,四边形为正方形,其中点A、C分别在x轴负半轴,y轴负半轴上,点B在第三象限内,点 , 点在函数的图像上 (1)、求k的值;(2)、连接 , 记的面积为S,设 , 求T的最大值.
(1)、求k的值;(2)、连接 , 记的面积为S,设 , 求T的最大值.