（华师大版）2023-2024学年八年级上学期数学微专题复习——多项式与多项式相乘

试卷更新日期：2023-06-30 类型：复习试卷

进入出卷网下载

一、选择题

1. 若 $(2 x - m) (x + 1)$ 的运算结果中不含 $x$ 的一次项，则 $m$ 的值等于（）

A、2 B、1 C、-1 D、-2

查看试题解析
2. 下列计算正确的是（）

A、m+m=m² B、(-3x)²=6x² C、(m+2n)²=m²+4n² D、(m+3)(m-3)=m²-9

查看试题解析
3. 若整式（2x+m）（x-1）不含x的一次项，则m的值为（　　）

A、-3 B、-2 C、-1 D、2

查看试题解析
4. 若多项式 $x^{2} + b x + c$ 因式分解的结果为 $(x - 2) (x + 3)$ ，则 $b + c$ 的值为（）

A、 $- 5$ B、 $- 1$ C、5 D、6

查看试题解析
5. 若多项式 $2 x^{2} + a x - 6$ 能分解成两个一次因式的积，且其中一个次因式 $2 x - 3$ ，则 $a$ 的值为（）

A、1 B、5 C、-1 D、-5

查看试题解析
6. 已知多项式 $a x^{2} + b x + c$ ，其因式分解的结果是 $(x + 1) (x - 4)$ ，则 $a b c$ 的值为（）

A、12 B、-12 C、6 D、-6

查看试题解析
7. 如图，根据需要将一块边长为x的正方形铁皮按如图的方法截去一部分后制成的长方形铁皮（阴影部分）的面积是多少？几名同学经过讨论给出了不同的答案，其中正确的是（）
①（x-5）（x-6）；②x²-5x-6（x-5）；③x²-6x-5x；④x²-6x-5（x-6）

A、①②④ B、①②③④ C、① D、②④

查看试题解析
8. 若 $(x - 1) (x^{2} + a x + 2)$ 的展开式中不含 $x^{2}$ ，则 $a$ 的值（）

A、-2 B、-1 C、0 D、1

查看试题解析
9. 若 $(2 x - 3) (x + 2) = 2 x^{2} + m x + n$ ，则m与n的值分别是（　　）

A、 $- 1 ， 6$ B、1 $， - 6$ C、 $- 3 ， - 2$ D、 $- 3 ， 2$

查看试题解析
10. 已知 $(x + 3) (x - 2) = x^{2} + b x + c$ ，那么 $b$ 、 $c$ 的值分别是（）

A、 $b = 1$ ， $c = - 6$ B、 $b = 1$ ， $c = 6$ C、 $b = 5$ ， $c = - 6$ D、 $b = 5$ ， $c = 6$

查看试题解析

二、填空题

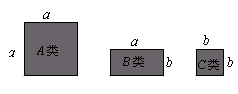
11. 实数a，b满足 $(a^{2} + 4) (b^{2} + 1) = 5 (2 a b - 1)$ ，则分式 $a (b + \frac{1}{b})$ 的值是.

查看试题解析
12. 已知二次三项式 $a x^{2} + b x + 1$ 与 $2 x^{2} - 3 x + 1$ 的乘积展开式中不含 $x^{3}$ 项，也不含 $x$ 项，则 $a - b =$ .

查看试题解析
13. 用图中所示的正方形和长方形卡片若干张，拼成一个长为2a+b，宽为3a+2b的矩形，需要A类卡片张，B类卡片张，C类卡片张．

查看试题解析
14. 若 $a - b = \sqrt{2} - 1$ ， $a b = \sqrt{2}$ ，则代数式 $(1 - a) (b + 1)$ 的值为．

查看试题解析
15. 阅读理解：如果一个数的平方等于﹣1，记为i²＝﹣1，i叫做虚数单位，我们把形如a+bi（a、b为实数，且b≠0）的数叫做复数，其中a叫这个复数的实部，b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.
如：（4+i）+（6﹣2i）＝（4+6）+（1﹣2）i＝10﹣i；

（2﹣i）（3+i）＝2×3+2i﹣3i﹣i²＝6﹣i﹣（﹣1）＝7﹣i.

根据以上信息，计算（3+i）（1﹣3i）＝.

查看试题解析

三、解答题

16. 已知 $(x^{2} + 2 x + a) (x + b)$ 中不含 $x^{2}$ 项和x项，求a，b的值．

查看试题解析
17. 仔细阅读下面例题，解答问题：
例题：已知二次三项式 $x^{2} - 4 x + m$ 有一个因式是 $(x + 3)$ ，求另一个因式以及 $m$ 的值．
解：设另一个因式为 $(x + n)$ ，得
$x^{2} - 4 x + m = (x + 3) (x + n)$
则 $x^{2} - 4 x + m = x^{2} + (n + 3) x + 3 n$
∴ ${\begin{array}{l} n + 3 = - 4 \\ m = 3 n \end{array}$
解得： $n = - 7$ ， $m = - 21$
∴另一个因式为 $(x - 7)$ ， $m$ 的值为 $- 21$
问题：仿照以上方法解答下面问题：
已知二次三项式 $2 x^{2} - 3 x - k$ 有一个因式是 $(2 x - 5)$ ，求另一个因式以及 $k$ 的值．

查看试题解析
18.
①先化简，再求值： (a²b-2ab²-b³)÷b-(a-b)(a+b)，其中a=-2， $b = \frac{1}{2}$ .

②若x²+ax+8和多项式x²-3x+b相乘的积中不含x³、x²项，求ab的值.

查看试题解析
19. 若x²＋px＋q与x²－3x＋2的乘积中不含x³项和x²项．求p、q的值．

查看试题解析

四、综合题

20. 在计算 $(x + a) (x + b)$ 时，甲把错b看成了6，得到结果是： $x^{2} + 8 x + 12$ ；乙错把a看成了-a，得到结果： $x^{2} + x - 6$ .

(1)、求出 $a ， b$ 的值；

(2)、在（1）的条件下，计算 $(x + a) (x + b)$ 的结果.

查看试题解析
21. 已知x≠1．观察下列等式：
(1-x)(1+x)=1-x² ；

(1-x)(1+x+x²)=1-x³；

(1-x)(1+x+x²+x³)=1-x⁴；

(1)、猜想： (1-x)(1+x+x²+x³+……+x^n-1)=；

(2)、证明你在(1)中的猜想；

(3)、根据你的猜想计算：(x-1)(x²⁰²³+x²⁰²²+x²⁰²¹+……+x²+x+1)．

查看试题解析
22. 甲乙两人共同计算一道整式乘法题 $(2 x + a) (3 x + b)$ .甲由于把第一个多项式中的“ $+ a$ ”看成了“ $- a$ ”，得到的结果为 $6 x^{2} + 11 x - 10$ .乙由于漏抄了第二个多项式中 $x$ 的系数，得到的结果为 $2 x^{2} - 9 x + 10$ .

(1)、求正确的 $a$ 、 $b$ 的值；

(2)、计算出这道整式乘法题的正确结果.

查看试题解析
23. 学习了平方差、完全平方公式后，小聪同学对学习和运用数学公式非常感兴趣，他通过上网查阅，发现还有很多数学公式，如立方和公式：（a＋b）（a²－ab＋b²）＝a³＋b³ ，他发现，运用立方和公式可以解决很多数学问题，请你也来试试利用立方和公式解决以下问题：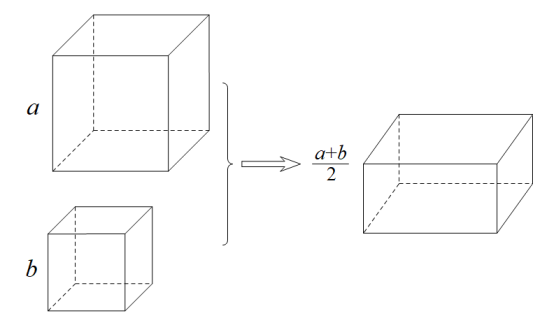

(1)、【公式理解】公式中的字母可以代表任何数、字母或式子
①化简：（a－b）（a²＋ab＋b²）＝；
②计算：（99³＋1）÷（99²－99＋1）＝；

(2)、【公式运用】已知： $\frac{1}{x}$ ＋x＝5，求 $[(\frac{1}{x})^{2} + x] \div (\frac{1}{x} + 1)$ 的值：

(3)、【公式应用】如图，将两块棱长分别为a、b的实心正方体橡皮泥揉合在一起，重新捏成一个高为 $\frac{a + b}{2}$ 的实心长方体，问这个长方体有无可能是正方体，若可能，a与b应满足什么关系？若不可能，说明理由.

查看试题解析