（华师大版）2023-2024学年八年级上学期数学微专题复习——单项式与多项式相乘

试卷更新日期：2023-06-30 类型：复习试卷

进入出卷网下载

一、选择题

1. 计算： $x (x^{2} - 1) =$ （　　）

A、 $x^{3} - 1$ B、 $x^{3} - x$ C、 $x^{3} + x$ D、 $x^{2} - x$

查看试题解析
2. 下列各式中，计算正确的是（）

A、 $x^{2} + 2 x^{2} = - 2 x^{4}$ B、 ${(3 x^{2} y^{3})}^{2} = 6 x^{4} y^{6}$ C、 ${(- x^{3})}^{3} = - x^{9}$ D、 $x^{2} (x - 1) = x^{3} - 1$

查看试题解析
3. 下列计算不正确的是（）

A、 $3 x y - (x^{2} - 2 x y) = 5 x y - x^{2}$ B、 $2 a^{2} b \cdot 4 a b^{3} = 8 a^{3} b^{4}$ C、 $5 x \cdot (2 x^{2} - y) = 10 x^{3} - 5 x y$ D、 $(x + 3) (x^{2} - 3 x + 9) = x^{3} + 9$

查看试题解析
4. 如果 $(2 n x + 3 x^{2} + m x^{3}) (- 4 x^{2})$ 的结果中不含x的五次项，那么m的值为（）

A、1 B、0 C、-1 D、 $- \frac{1}{4}$

查看试题解析
5. 下列计算中错误的是（　　）

A、4a⁵b³c²÷（﹣2a²bc）²＝ab B、（a+1）（a﹣1）（a²+1）＝a⁴﹣1 C、4x²y•（﹣ $\frac{1}{2}$ y）÷4x²y²＝﹣ $\frac{1}{2}$ D、25×（ $\frac{1}{25}$ x²﹣ $\frac{1}{10}$ x+1）＝x²﹣ $\frac{5}{2}$ x+1

查看试题解析
6. 若(ax-b)(3x+4)=bx²+cx+72，则a+b+c的值为（）

A、-6 B、6 C、18 D、36

查看试题解析
7. 一长方形操场，其中一边长为 $2 a + b$ ，另一边长为 $a$ ，则该操场的面积为（）

A、 $3 a + b$ B、 $6 a + 2 b$ C、 $2 a^{2} + a b$ D、 $2 a^{2} b$

查看试题解析
8. 在一次数学课上，学习了单项式乘多项式，小明回家后，拿出课堂笔记本复习，发现这样一道题： $- 3 x (- 2 x^{2} + 3 x - 1) = 6 x^{3} + □ + 3 x$ ，“□”的地方被墨水污染了，你认为“□”内应填写（）

A、 $9 x^{2}$ B、 $- 9 x^{2}$ C、 $9 x$ D、 $- 9 x$

查看试题解析
9. 今天数学课上，老师讲了单项式乘多项式，放学回到家，小明拿出课堂笔记复习，发现一道题： $- 7 x y (2 y - x - 3) = - 14 x y^{2} + 7 x^{2} y$ □，□的地方被钢笔水弄污了，你认为□内应填写（）

A、 $+ 21 x y$ B、 $- 21 x y$ C、-3 D、 $- 10 x y$

查看试题解析
10. 一个长方体的长、宽、高分别为3a－4，2a，a，它的体积等于（）

A、3a³－4a² B、a² C、6a³－8a² D、6a³－8a

查看试题解析

二、填空题

11. 计算： $2 a b (3 a^{2} - 5 b) =$ ．

查看试题解析
12. 下列计算算式中：① ${(- 2 x^{3} y^{2})}^{3} = - 6 x^{9} y^{6}$ ，② $a (a^{2} - 1) = a^{3} - 1$ ，③ ${(- 2)}^{2020} \times {(\frac{1}{2})}^{2019} = 2$ ，④ $(a + b) (a - 2 b) = a^{2} - a b - 2 b^{2}$ ，⑤ $- 2 a \cdot {(a^{2})}^{3} = - 2 a^{9}$ ，正确的是.（填序号）

查看试题解析
13. 若 $a (a - 1) - (a^{2} - b) = - 2$ ，则 $\frac{a^{2} + b^{2}}{2} - a b$ 的值为．

查看试题解析
14. 计算 $- 5 x^{2} y (\frac{2}{5} x - 2 y^{2}) =$ .

查看试题解析
15. 若 3x(x+1)＝mx²+nx，则 m+n＝.

查看试题解析

三、解答题

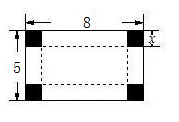
16. 某学生在计算一个多项式乘3ac时错误地算成了加上3ac，得到的答案是3bc－3ac－2ab，那么正确的计算结果应是多少？

查看试题解析
17. 如图，在长8cm，宽5cm的长方形塑料板的四个角剪去4个边长为 $x cm$ 的小正方形，按折痕做一个无盖的长方体盒子，求盒子的容积（塑料板的厚度忽略不计）.

查看试题解析
18. 一块长方形硬纸片，长为(5a²＋4b²)m，宽为6a⁴m，在它的四个角上分别剪去一个边长为 $\frac{3}{2}$ a³m的小正方形然后折成一个无盖的盒子，请你求这个无盖盒子的表面积．

查看试题解析
19. 先化简，再求值：（x+y）²﹣y（2x+y）﹣8y，其中x=﹣1，y=2．

查看试题解析

四、综合题

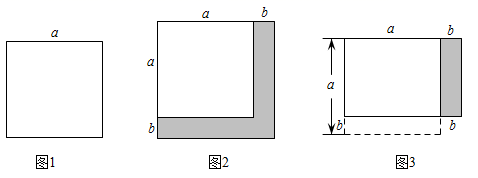
20. 某地产公司为了吸引年轻人购房，持推出“主房+多变入户花园”的两种户型．即在图1中边长为a米的正方形主房进行改造．
户型一是在主房两侧均加长b米（0＜9b＜a）．阴影部分作为入户花园，如图2所示．
户型二是在主房一边减少b米后，另一边再增加b米，阴影部分作为入户花园．如图3所示．
解答下列问题：

(1)、设两种户型的主房面积差为M，入户花园的面积差为N，试比较M和N的大小．

(2)、若户型一的总价为50万元，户型二的总价为40万元，试判断哪种户型单价较低，并说明理由．

查看试题解析
21. 阅读下列文字，并解决问题．
已知x²y＝3，求2xy（x⁵y²﹣3x³y﹣4x）的值．

我们知道，满足x²y＝3的x，y的值可能较多，不可能逐一代入求解，而运用整体思想能使问题化繁为简，化难为易，运用整体代入的方法能巧妙地解决一些代数式的求值问题，于是将x²y＝3整体代入．

解：2xy（x⁵y²﹣3x³y﹣4x）

＝2x⁶y³﹣6x⁴y²﹣8x²y

＝2（x²y）³﹣6（x²y）²﹣8x²y

＝2×3³﹣6×3²﹣8×3

＝﹣24．

请你用上述方法解决问题：

(1)、已知ab＝4，求（2a³b²﹣3a²b+4a）•（﹣2b）的值；

(2)、已知x﹣ $\frac{1}{x}$ ＝5，求 $x + \frac{1}{x}$ 的值．

查看试题解析
22. 如图，长为 $60 cm$ ，宽为 $x (cm)$ 的大长方形被分割为 $7$ 小块，除阴影 $A$ ， $B$ 外，其余 $5$ 块是形状、大小完全相同的小长方形，其较短一边长为 $y (cm)$ ．

(1)、每个小长方形较长的一边长是 $cm$ （用含 $y$ 的代数式表示）.

(2)、分别用含 $x$ ， $y$ 的代数式表示阴影 $A$ ， $B$ 的面积，并计算阴影 A 的面积与阴影B的面积的差.

(3)、当 $y = 10$ 时，阴影 $A$ 与阴影 $B$ 的面积差会随着 $x$ 的变化而变化吗?请你作出判断，并说明理由.

查看试题解析
23.
一条防洪堤坝，其横断面是梯形，上底宽米，下底宽米，坝高米．

(1)、求防洪堤坝的横断面积；

(2)、如果防洪堤坝长100米，那么这段防洪堤坝的体积是多少立方米？

查看试题解析