2023年浙江省七升八尖子暑假大练兵之几何图形
试卷更新日期:2023-06-30 类型:复习试卷
一、选择题
-
1. 一副三角板按如图所示叠放在一起,其中点、重合,若固定三龟板 , 三角板绕点在平面内旋转,当( )时, .
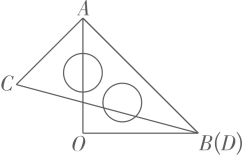 A、 B、或 C、或 D、或2. 如图, , , , , 给出以下结论: ; ; ; . 其中正确的结论有( )
A、 B、或 C、或 D、或2. 如图, , , , , 给出以下结论: ; ; ; . 其中正确的结论有( )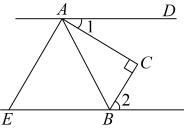 A、1个 B、2个 C、3个 D、4个3. 如图,已知 , , 点是射线上一动点(与点不重合),、分别平分和 , 分别交射线于点、 , 下列结论:①;②;③当时,;④当点运动时,的数量关系不变.其中正确结论有( )个.
A、1个 B、2个 C、3个 D、4个3. 如图,已知 , , 点是射线上一动点(与点不重合),、分别平分和 , 分别交射线于点、 , 下列结论:①;②;③当时,;④当点运动时,的数量关系不变.其中正确结论有( )个.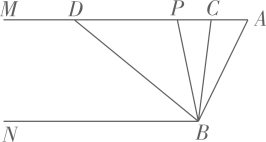 A、1 B、2 C、3 D、44. 某同学在一次数学实践活动课中将-条对边互相平行的纸带进行两次折叠(如图) .折痕分别为AB,CD,若CD∥BE,且∠CBE=∠ABC,则∠1为( )
A、1 B、2 C、3 D、44. 某同学在一次数学实践活动课中将-条对边互相平行的纸带进行两次折叠(如图) .折痕分别为AB,CD,若CD∥BE,且∠CBE=∠ABC,则∠1为( )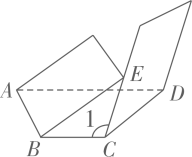 A、106° B、108° C、109° D、110°5. 如图,AB∥EF,∠C=90°,则α、β、γ的关系为( )
A、106° B、108° C、109° D、110°5. 如图,AB∥EF,∠C=90°,则α、β、γ的关系为( )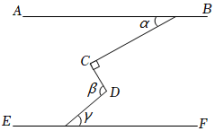 A、α+β-γ=90° B、β=α+γ C、α+β+γ=180° D、β+γ-α=90°6. 如图, , , 平分 , 平分 , 则( )
A、α+β-γ=90° B、β=α+γ C、α+β+γ=180° D、β+γ-α=90°6. 如图, , , 平分 , 平分 , 则( )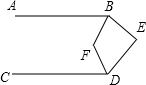 A、 B、 C、 D、7. 如图,已知直线AB,CD被直线AC所截, , E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β,下列各式:①β﹣α,②α﹣β,③180°﹣α+β,④360°﹣α﹣β,可以表示∠AEC的度数的有( )
A、 B、 C、 D、7. 如图,已知直线AB,CD被直线AC所截, , E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β,下列各式:①β﹣α,②α﹣β,③180°﹣α+β,④360°﹣α﹣β,可以表示∠AEC的度数的有( )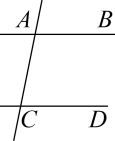 A、③④ B、①③④ C、①②④ D、②③④8. 如图,已知直线AB、CD被直线AC所截,// , E是平面内任意一点(点E不在直线AB、CD、AC上),设 , . 下列各式:① , ② , ③ , ④ , 的度数可能是( )
A、③④ B、①③④ C、①②④ D、②③④8. 如图,已知直线AB、CD被直线AC所截,// , E是平面内任意一点(点E不在直线AB、CD、AC上),设 , . 下列各式:① , ② , ③ , ④ , 的度数可能是( )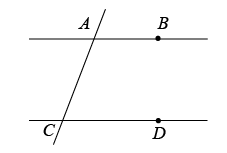 A、①②③ B、①②④ C、②③④ D、①②③④9. 如图, , ∠M=44°,AN平分∠BAM,CN平分∠DCM,则∠N等于( )
A、①②③ B、①②④ C、②③④ D、①②③④9. 如图, , ∠M=44°,AN平分∠BAM,CN平分∠DCM,则∠N等于( )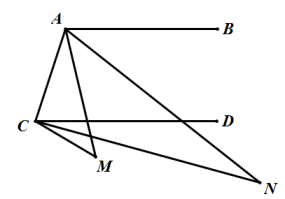 A、21.5° B、21° C、22.5° D、22°10. 一张长方形纸条按如图所示折叠,EF是折痕,若∠EFB=35°,则:①∠GEF=35°;②∠EGB=70°;③∠AEG=110°;④=70°.以上结论正确的有( )
A、21.5° B、21° C、22.5° D、22°10. 一张长方形纸条按如图所示折叠,EF是折痕,若∠EFB=35°,则:①∠GEF=35°;②∠EGB=70°;③∠AEG=110°;④=70°.以上结论正确的有( )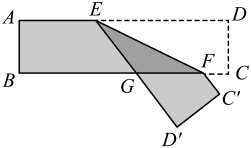 A、① ② ③ ④ B、② ③ ④ C、① ② ③ D、① ②
A、① ② ③ ④ B、② ③ ④ C、① ② ③ D、① ②二、填空题
-
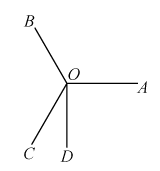
11. 如图, , 射线在内部, , 则度.
 12. 已知线段AB=12,C是线段AB上一点,且BC=2,点D在射线AB上,若DA=4DC,则BD的长为.13. 将相同的长方形卡片按如图方式摆放在一个直角上,每个长方形卡片长为2,宽为1,依此类推,摆放2023个时,实线部分长为.
12. 已知线段AB=12,C是线段AB上一点,且BC=2,点D在射线AB上,若DA=4DC,则BD的长为.13. 将相同的长方形卡片按如图方式摆放在一个直角上,每个长方形卡片长为2,宽为1,依此类推,摆放2023个时,实线部分长为.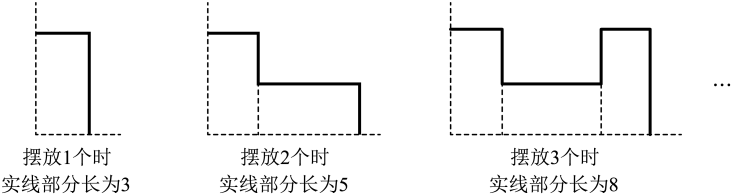 14. 如图,点B在线段上,已知 , , 点O是线段的中点,则线段
14. 如图,点B在线段上,已知 , , 点O是线段的中点,则线段cm.
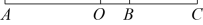 15. 如图,线段 BD =AB=CD, 点 M、N分别是线段AB、CD的中点,且MN = 20cm, 则 AC的长为 .
15. 如图,线段 BD =AB=CD, 点 M、N分别是线段AB、CD的中点,且MN = 20cm, 则 AC的长为 .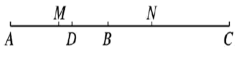 16. 如图,将三个形状,大小完全一样的正方形的一个顶点重合放置, , , 则度.
16. 如图,将三个形状,大小完全一样的正方形的一个顶点重合放置, , , 则度.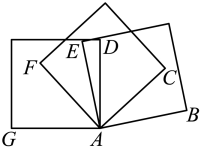 17. 如图,已知DEBC,BE平分∠ABC,若∠1=70°,则∠AEB的度数为.
17. 如图,已知DEBC,BE平分∠ABC,若∠1=70°,则∠AEB的度数为.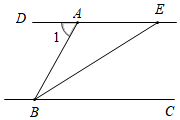 18. 如图,OA⊥OB, OB平分∠COD,若∠BOC=31°30',则∠AOD的度数为 . (结果用度表示)
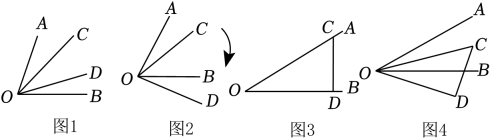
18. 如图,OA⊥OB, OB平分∠COD,若∠BOC=31°30',则∠AOD的度数为 . (结果用度表示)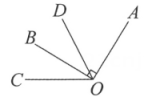 19. 如图1,一款暗插销由外壳 , 开关 , 锁芯DE三部分组成,其工作原理如图2,开关绕固定点O转动,由连接点D带动锁芯DE移动.图3为插销开启状态,此时连接点D在线段上,如位置.开关绕点O顺时针旋转180°后得到 , 锁芯弹回至位置(点B与点重合),此时插销闭合如图4.已知 , , 则mm.
19. 如图1,一款暗插销由外壳 , 开关 , 锁芯DE三部分组成,其工作原理如图2,开关绕固定点O转动,由连接点D带动锁芯DE移动.图3为插销开启状态,此时连接点D在线段上,如位置.开关绕点O顺时针旋转180°后得到 , 锁芯弹回至位置(点B与点重合),此时插销闭合如图4.已知 , , 则mm.
 20. 有一无弹性细线,拉直时测得细线长为 , 现进行如下操作:1.在细线上任取一点;2.将细线折叠,使点与点重合,记折点为点;3.将细线折叠,使点与点重合,记折点为点.
20. 有一无弹性细线,拉直时测得细线长为 , 现进行如下操作:1.在细线上任取一点;2.将细线折叠,使点与点重合,记折点为点;3.将细线折叠,使点与点重合,记折点为点. (1)、如图,的长为;(2)、继续进行折叠,使点与点重合,并把点和与其重叠的点处的细线剪开,使细线分成长为 , , 的三段 , 当 , 则细线未剪开时的长为.
(1)、如图,的长为;(2)、继续进行折叠,使点与点重合,并把点和与其重叠的点处的细线剪开,使细线分成长为 , , 的三段 , 当 , 则细线未剪开时的长为.三、解答题
-
21. 点A,B,C在直线l上,若AB=4cm,BC=3cm,点O是线段AC的中点,那么线段OB的长是多少?
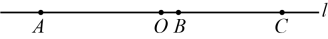
小明同学根据下述图形对这个题目进行了求解:
∵A,B,C三点顺次在直线l上,
∴AC=AB+BC,
∵AB=4cm,BC=3cm,
∴AC=7cm,
又∵点O为线段AC的中点,
∴AO=AC=×7=3.5cm,
∴OB=AB﹣AO=4﹣3.5=0.5cm.
小明考虑得全面吗?如果不全面,请补全解题过程,如果全面,请说明理由.
22. 如图,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内部,∠BOE= ∠EOC,∠DOE=70°,求∠EOC的度数.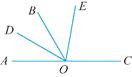
四、作图题
-
23. 如图,已知三个点A、B、C,按下列要求画图.
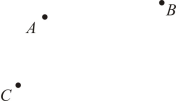
⑴画直线;
⑵画射线;
⑶过B点画直线的垂线段,垂足为F.(画图工具不限,不需写出结论,只需画出图形、标注字母)
24. 如图,已知直线l表示一段公路,点A表示学校,点B表示书店,点C表示图书馆.
⑴请画出学校A到书店B的最短路线.
⑵在公路l上找一个路口M,使得的值最小.
⑶现要从学校A向公路l修一条小路,怎样修路才能使小路的长最短?请画出小路的路线,并用所学知识描述小路的方向.25. 如图,在的正方形网格中,每个小正方形的顶点都称为格点,点A、B、C都在格点上.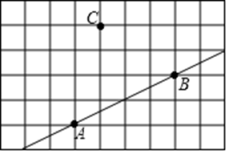 (1)、画射线;(2)、找一格点D,使得直线 , 画出直线;(3)、找一格点E,使得直线于点H,画出直线 , 并注明垂足H.
(1)、画射线;(2)、找一格点D,使得直线 , 画出直线;(3)、找一格点E,使得直线于点H,画出直线 , 并注明垂足H.五、综合题
-
26. 新定义:从一个角的顶点出发,在角的内部引两条射线,如果这两条射线所成的角等于这个角的一半,那么这两条射线所成的角叫做这个角的内半角.
如图1,若射线 , 在的内部,且 , 则是的内半角.
根据以上信息,解决下面的问题:
(1)、如图1, , , 若是的内半角,则 ;(2)、如图2,已知 , 将绕点按顺时针方向旋转一个角度()至.若是的内半角,求的值;(3)、把一块含有角的三角板按图3方式放置.使边与边重合,边与边重合.如图4,将三角板绕顶点以3度/秒的速度按顺时针方向旋转一周,旋转时间为秒,当射线、、、构成内半角时,直接写出的值.27. 如图,已知 , 为锐角,平分 , 射线在内部.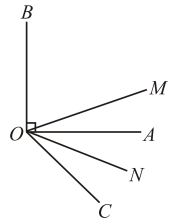 (1)、图中共有多少个小于平角的角?(2)、若 , , 求的度数.(3)、若 , , 请通过计算判断与的关系.
(1)、图中共有多少个小于平角的角?(2)、若 , , 求的度数.(3)、若 , , 请通过计算判断与的关系.