2023年浙江省七升八尖子暑假大练兵之数与式

试卷更新日期：2023-06-30 类型：复习试卷

进入出卷网下载

一、选择题

1. 在多项式 $x - y - z - m - n$ （其中 $x > y > z > m > n$ ）中，对相邻的两个字母间任意添加绝对值符号，添加绝对值符号后仍只有减法运算，然后进行去绝对值运算，称此为“绝对操作”．例如： $x - y - | z - m | - n = x - y - z + m - n$ ， $| x - y | - z - | m - n | = x - y - z - m + n$ ， ……．
下列说法：

①存在“绝对操作”，使其运算结果与原多项式相等；

②不存在“绝对操作”，使其运算结果与原多项式之和为 $0$ ；

③所有的“绝对操作”共有 $7$ 种不同运算结果．

其中正确的个数是（）

A、 $0$ B、 $1$ C、 $2$ D、 $3$

查看试题解析
2. 定义：如果代数式 $A = a_{1} x^{2} + b_{1} x + c_{1}$ ( $a_{1} \neq 0$ ， $a_{1}$ ， $b_{1}$ ， $c_{1}$ 是常数)与 $B = a_{2} x^{2} + b_{2} x + c_{2}$ ( $a_{2} \neq 0$ ， $a_{2}$ ， $b_{2}$ ， $c_{2}$ 是常数)，满足 $a_{1} + a_{2} = 0$ ， $b_{1} + b_{2} = 0$ ， $c_{1} + c_{2} = 0$ ，则称这两个代数式 $A$ 与 $B$ 互为“和谐式”，对于上述“和谐式” $A$ 、 $B$ ，下列三个结论正确的个数为（）
①若 $A = - x^{2} - \frac{4}{3} m x - 2$ ， $B = x^{2} - 2 n x + n$ ，则 $(m + n)^{2023}$ 的值为-1；
②若 $k$ 为常数，关于 $x$ 的方程 $A = k$ 与 $B = k$ 的解相同，则 $k = 0$ ；
③若 $p$ ， $q$ 为常数， $p A + q B$ 的最小值为 $p - q$ ，则 $A$ 有最小值，且最小值为1.

A、0个 B、1个 C、2个 D、3个

查看试题解析
3. 如图，点A在数轴上表示的数是-8，点B在数轴上表示的数是16．若点A以6个单位长度/秒的速度向右匀速运动，同时点B以2个单位长度/秒的速度向左匀速运动．问：当AB＝8时，运动时间为多少秒？（）

A、2秒 B、13.4秒 C、2秒或4秒 D、2秒或6秒

查看试题解析
4. 已知 $a_{1} + a_{2} = 1$ ， $a_{2} + a_{3} = 2$ ， $a_{3} + a_{4} = - 3$ ， $a_{4} + a_{5} = - 4$ ， $a_{5} + a_{6} = 5$ ， $a_{6} + a_{7} = 6$ ， $a_{7} + a_{8} = - 7$ ， $a_{8} + a_{9} = - 8$ ， ……， $a_{99} + a_{100} = - 99$ ， $a_{100} + a_{1} = - 100$ ， $a_{1} + a_{2} + a_{3} + ⋯ ⋯ + a_{100}$ 的值为（）

A、-48 B、-50 C、-98 D、-100

查看试题解析
5. 九宫格起源于中国古代的神秘图案河图和洛书.如图，将 $3$ ， $2$ ， $1$ ， $0$ ， $- 1$ ， $- 2$ ， $- 3$ ， $- 4$ ， $- 5$ 填入九宫格内，使每行、每列、每条对角线上三个数的和都相等，则 $a$ 的值为（）

A、 $- 2$ B、 $- 3$ C、 $- 4$ D、 $- 5$

查看试题解析
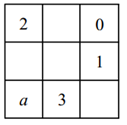6. 一只小球落在数轴上的某点 $P_{0}$ ，第一次从 $P_{0}$ 向左跳1个单位到 $P_{1}$ ，第二次从 $P_{1}$ 向右跳2个单位到 $P_{2}$ ，第三次从 $P_{2}$ 向左跳3个单位到 $P_{3}$ ，第四次从 $P_{3}$ 向右跳4个单位到 $P_{4}$ ……若按以上规律跳了100次时，它落在数轴上的点 $P_{100}$ 所表示的数恰好是2022，则这只小球的初始位置点 $P_{0}$ 所表示的数是（）

A、 $- 1971$ B、1971 C、 $- 1972$ D、1972

查看试题解析
7. 一电子跳蚤落在数轴上的某点k₀处，第一步从k₀向左跳一个单位到k₁ ，第二步从k₁向右跳2个单位到k₂ ，第三步由k₂处向左跳3个单位到k₃ ，第四步由k₃向右跳4个单位k₄ ， ….按以上规律跳了100步后，电子跳蚤落在数轴上的数是0，则k₀表示的数是

A、0 B、100 C、50 D、 $- 50$

查看试题解析
8. 若 $m \cdot n \neq 0$ ，则 $\frac{| m |}{m} + \frac{| n |}{n} + \frac{| m n |}{m n}$ 的取值可能是（）.

A、±3 B、±1或±3 C、±1 D、-1或3

查看试题解析
9. 正整数按如图的规律排列，则2022位于哪一行，哪一列（）

A、第45行第4列 B、第4行第45列 C、第46行第3列 D、第3行第46列

查看试题解析
10. 将－5，－4，－3，－2，－1，0，1，2，3填入九宫格内，使每行、每列、每条斜对角线上的3个数和都相等，如图所示的x处应填（）

A、－5 B、－4 C、－3 D、－2

查看试题解析

二、填空题

11. 为了求 $1 + 3 + 3^{2} + 3^{3} + \cdot \cdot \cdot + 3^{100}$ 的值，可令 $M = 1 + 3 + 3^{2} + 3^{3} \cdot \cdot \cdot + 3^{100}$ ，则 $3 M = 3 + 3^{2} + 3^{3} + 3^{4} + \cdot \cdot \cdot 3^{101}$ ，因此， $3 M - M = 3^{101} - 1$ ，所以 $M = \frac{3^{101} - 1}{2}$ 即 $1 + 3 + 3^{2} + 3^{3} \cdot \cdot \cdot + 3^{100} = \frac{3^{101} - 1}{2}$ ，依照以上推理计算： $1 + 5 + 5^{2} + 5^{3} + \cdot \cdot \cdot + 5^{2023}$ 的值是．

查看试题解析
12. 已知m为整数，若m+2023，4m-2023的值都是整数的平方，则满足条件的m的最小值为．

查看试题解析
13. 实数a，b满足 $| a + 1 | + | 2 - a | = 8 - | b + 3 | - | b + 8 |$ ，则 $a + b$ 的最小值为.

查看试题解析
14. 如图，已知数轴上的点 $C$ 表示的数为6，点 $A$ 表示的数为 $- 4$ ，点 $B$ 是 $A C$ 的中点，动点 $P$ 从点 $A$ 出发，以每秒2个单位长度的速度沿数轴向右匀速运动，运动时间为 $t$ 秒（ $t > 0$ ），另一动点 $Q$ ，从 $B$ 出发，以每秒1个单位长度的速度沿数轴向左匀速运动，且 $P$ ， $Q$ 同时出发，当 $t$ 为秒时，点 $P$ 与点 $Q$ 之间的距离为2个单位长度.

查看试题解析
15. 如图，数轴上放置的正方形的周长为 $8$ 个单位，它的两个顶点A、 $B$ 分别与数轴上表示 $- 1$ 和 $- 3$ 的两个点重合．现将该正方形绕顶点按顺时针方向在数轴上向右无滑动的翻滚，当正方形翻滚一周后，点A落在数轴上所对应的数为 $7$ ．

(1)、当正方形翻滚三周后，点A落在数轴上所对应的数为；

(2)、如此继续下去，当正方形翻滚 $n$ 周后 $(n$ 表示正整数 $)$ ，用含 $n$ 的式子表示点A落在数轴上所对应的数为．

查看试题解析

16. 张老师准备为书法兴趣小组的同学购买上课的用具，在文具商店看到商店有A、B两种组合和C、D、E、F商品及它们的售价，组合及单件商品质量一样，若该小组共有12人，其中，笔和本每人各需要一份，砚台2人一方即可，墨汁n瓶（

n \geq 3

）．张老师共带了200元钱，请给出一个满足条件的购买方案（购买数量写前面商品代码写后面即可，例如：2A+3B+...；n最多买瓶．

商品	价格
组合A（1支笔＋1个本＋1方砚台＋1瓶墨汁）	25元
组合B（1支笔＋1个本＋1瓶墨汁）	18元
C：1支笔	5元
D：1个本	4元
E：一方砚台	10元
F：一瓶墨汁	12元

查看试题解析

17. 如图，数轴上O，A两点的距离为4，一动点P从点A出发，第1次跳动到 $A O$ 的中点 $A_{1}$ 处，第2次从点 $A_{1}$ 跳动到 $A_{1} O$ 的中点 $A_{2}$ 处，第3次从点 $A_{2}$ 跳动到 $A_{2} O$ 的中点 $A_{3}$ 处，按照这样的规律继续跳动到点 $A_{4}$ ， $A_{5}$ ， $A_{6}$ ， …， $A_{n}$ 处，那么线段 $A_{n} A$ 的长度为．

查看试题解析
18. 已知 $x ， y ， z$ 都是有理数， $x + y + z = 0$ ， $x y z \neq 0$ ，则 $\frac{| x |}{y + z} + \frac{| y |}{x + z} + \frac{| z |}{x + y}$ 的值是．

查看试题解析
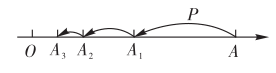19. “转化”是一种解决问题的常用测量，有时画图可以帮助我们找到转化的方法。例如借助图①，可以把算式1+3+5+7+9+11转化为6²=36.请你观察图②，利用转化的方法计算： $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{128} =$ .

查看试题解析
20. 【阅读】 $| 4 - 1 |$ 表示4与1两数在数轴上所对应的两点之间的距离： $| 4 + 1 |$ 可以看做 $| 4 - (- 1) |$ ，表示4与 $- 1$ 两数在数轴上所对应的两点间的距离．

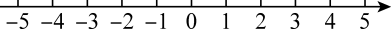(1)、 $| 4 - (- 1) | =$ ；

(2)、在数轴上，有理数5与 $- 3$ 所对应的两点之间的距离为；

(3)、结合数轴找出所有符合条件的整数 $x$ ，使得 $| x + 1 | = 3$ ，则 $x =$ ；

(4)、利用数轴分析，若 $x$ 是整数，且满足 $| x + 3 | + | x - 2 | = 5$ ，则满足条件的所有 $x$ 的值的和为．

查看试题解析

三、计算题

21. 计算： $\sqrt[3]{- 27} - \sqrt{5^{2} - 4^{2}} + (- 1)^{2022} + (\frac{1}{4})^{- 1} - 202 2^{0}$ ．

查看试题解析
22. $\frac{\frac{1}{3}}{(1 + \frac{1}{2}) (1 + \frac{1}{3})} + \frac{\frac{1}{4}}{(1 + \frac{1}{2}) (1 + \frac{1}{3}) (1 + \frac{1}{4})} + \dots +$ $\frac{\frac{1}{2021}}{(1 + \frac{1}{2}) (1 + \frac{1}{3}) (1 + \frac{1}{4}) \dots (1 + \frac{1}{2021})}$

查看试题解析
23. 请先阅读下列一段内容，然后解答问题：
因为： $\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ， $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ，…… ， $\frac{1}{9 \times 10} = \frac{1}{9} - \frac{1}{10}$ ，

所以： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{9 \times 10}$

$= (1 - \frac{1}{2}) + (\frac{1}{2} - \frac{1}{3}) + (\frac{1}{3} - \frac{1}{4}) + \dots + (\frac{1}{9} - \frac{1}{10})$

$= 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \dots + \frac{1}{9} - \frac{1}{10} = 1 - \frac{1}{10} = \frac{9}{10}$

计算：

(1)、 $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{2007 \times 2008}$ ；

(2)、 $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + \dots + \frac{1}{49 \times 51}$ .

查看试题解析
24. 定义新运算“ $@$ ”与“ $\oplus$ ”： $a @ b = \frac{a + b}{2}$ ， $a \oplus b = \frac{a - b}{2}$

(1)、计算的值 $[3 @ (- 2)] - [(- 2) \oplus (- 1)]$ ；

(2)、若 $A = [3 b @ (- a)] + [a \oplus (2 - 3 b)]$ ， $B = [a @ (- 3 b)] + [(- a) \oplus (- 2 - 9 b)]$ ，求 $A + B$ 的值.

查看试题解析
25. 若（2a-1）²+|2a+b|=0，且|c-1|=2，求c·（a³-b）的值

查看试题解析
26. 观察 $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ =（1－ $\frac{1}{2}$ ）+（ $\frac{1}{2}$ － $\frac{1}{3}$ ）=1－ $\frac{1}{3}$ = $\frac{2}{3}$

(1)、计算： $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ +……+ $\frac{1}{2013 \times 2014}$

(2)、计算： $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + \dots \dots + \frac{1}{99 \times 101}$

查看试题解析