陕西省2023年中考数学试卷(A卷)
试卷更新日期:2023-06-29 类型:中考真卷
一、选择题(本大题共8小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 计算:( )A、 B、 C、 D、2. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图, , 若 , 则的度数为( )
3. 如图, , 若 , 则的度数为( ) A、 B、 C、 D、4. 计算:( )A、 B、 C、 D、5. 在同一平面直角坐标系中,函数和为常数,的图象可能是( )A、
A、 B、 C、 D、4. 计算:( )A、 B、 C、 D、5. 在同一平面直角坐标系中,函数和为常数,的图象可能是( )A、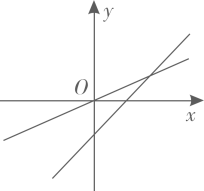 B、
B、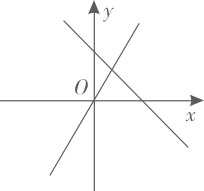 C、
C、 D、
D、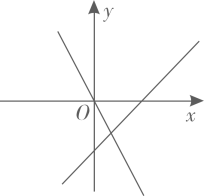 6. 如图,是的中位线,点在上,连接并延长,与的延长线相交于点若 , 则线段的长为( )
6. 如图,是的中位线,点在上,连接并延长,与的延长线相交于点若 , 则线段的长为( ) A、 B、 C、 D、7. 陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一图是从正面看到的一个“老碗”图的形状示意图.是的一部分,是的中点,连接 , 与弦交于点 , 连接 , 已知 , 碗深 , 则的半径为( )
A、 B、 C、 D、7. 陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一图是从正面看到的一个“老碗”图的形状示意图.是的一部分,是的中点,连接 , 与弦交于点 , 连接 , 已知 , 碗深 , 则的半径为( ) A、 B、 C、 D、8. 在平面直角坐标系中,二次函数为常数的图象经过点 , 其对称轴在轴左侧,则该二次函数有( )A、最大值 B、最大值 C、最小值 D、最小值
A、 B、 C、 D、8. 在平面直角坐标系中,二次函数为常数的图象经过点 , 其对称轴在轴左侧,则该二次函数有( )A、最大值 B、最大值 C、最小值 D、最小值二、填空题(本大题共5小题,共15.0分)
-
9. 如图,在数轴上,点表示 , 点与点位于原点的两侧,且与原点的距离相等,则点表示的数是 .
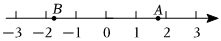 10. 如图,正八边形的边长为 , 对角线、相交于点则线段的长为 .
10. 如图,正八边形的边长为 , 对角线、相交于点则线段的长为 . 11. 点是菱形的对称中心, , 连接 , 则的度数为 .12. 如图,在矩形和正方形中,点在轴正半轴上,点 , 均在轴正半轴上,点在边上, , 若点 , 在同一个反比例函数的图象上,则这个反比例函数的表达式是 .
11. 点是菱形的对称中心, , 连接 , 则的度数为 .12. 如图,在矩形和正方形中,点在轴正半轴上,点 , 均在轴正半轴上,点在边上, , 若点 , 在同一个反比例函数的图象上,则这个反比例函数的表达式是 . 13. 如图,在矩形中, , 点在边上,且 , 、分别是边、上的动点,且 , 是线段上的动点,连接 , 若则线段的长为 .
13. 如图,在矩形中, , 点在边上,且 , 、分别是边、上的动点,且 , 是线段上的动点,连接 , 若则线段的长为 .
三、解答题(本大题共13小题,共81.0分。解答应写出文字说明,证明过程或演算步骤)
-
14. 解不等式:15. 计算: .16. 化简: .17. 如图已知角 , , 请用尺规作图法,在内部求作一点使且保留作图痕迹,不写作法
 18. 如图,在中, , 过点作 , 垂足为 , 延长至点使在边上截取 , 连接求证: .
18. 如图,在中, , 过点作 , 垂足为 , 延长至点使在边上截取 , 连接求证: .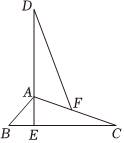 19. 一个不透明的袋子中装有四个小球,这四个小球上各标有一个数字,分别是 , , , 这些小球除标有的数字外都相同.(1)、从袋中机摸出一个小球,则摸出的这个小球上标有的数字是的概率为;(2)、先从袋中随机摸出一个小球,记下小球上标有的数字后,放回,摇匀,再从袋中随机摸出一个小球,记下小球上标有的数字,请利用画树状图或列表的方法、求摸出的这两个小球上标有的数字之积是偶数的概率.20. 小红在一家文具店买了一种大笔记本个和一种小笔记本个,共用了元已知她买的这种大笔记本的单价比这种小笔记本的单价多元,求该文具店中这种大笔记本的单价.21. 一天晚上,小明和爸爸带着测角仪和皮尺去公园测量一景观灯灯杆底部不可到达的高如图所示,当小明爸爸站在点处时,他在该景观灯照射下的影子长为 , 测得;当小明站在爸爸影子的顶端处时,测得点的仰角为已知爸爸的身高 , 小明眼睛到地面的距离 , 点、、在同一条直线上, , , 求该景观灯的高参考数据: , ,
19. 一个不透明的袋子中装有四个小球,这四个小球上各标有一个数字,分别是 , , , 这些小球除标有的数字外都相同.(1)、从袋中机摸出一个小球,则摸出的这个小球上标有的数字是的概率为;(2)、先从袋中随机摸出一个小球,记下小球上标有的数字后,放回,摇匀,再从袋中随机摸出一个小球,记下小球上标有的数字,请利用画树状图或列表的方法、求摸出的这两个小球上标有的数字之积是偶数的概率.20. 小红在一家文具店买了一种大笔记本个和一种小笔记本个,共用了元已知她买的这种大笔记本的单价比这种小笔记本的单价多元,求该文具店中这种大笔记本的单价.21. 一天晚上,小明和爸爸带着测角仪和皮尺去公园测量一景观灯灯杆底部不可到达的高如图所示,当小明爸爸站在点处时,他在该景观灯照射下的影子长为 , 测得;当小明站在爸爸影子的顶端处时,测得点的仰角为已知爸爸的身高 , 小明眼睛到地面的距离 , 点、、在同一条直线上, , , 求该景观灯的高参考数据: , , 22. 经验表明,树在一定的成长阶段,其胸径树的主干在地面以上处的直径越大,树就越高通过对某种树进行测量研究,发现这种树的树高是其胸径的一次函数已知这种树的胸径为时,树高为;这种铜的胸径为时,树高为 .(1)、求与之间的函数表达式;(2)、当这种树的胸径为时,其树高是多少?23. 某校数学兴趣小组的同学们从“校园农场“中随机抽取了棵西红柿植株,并统计了每棵植株上小西红柿的个数其数据如下: , , , , , , , , , , , , , , , , , , , 通过对以上数据的分析整理,绘制了统计图表:
22. 经验表明,树在一定的成长阶段,其胸径树的主干在地面以上处的直径越大,树就越高通过对某种树进行测量研究,发现这种树的树高是其胸径的一次函数已知这种树的胸径为时,树高为;这种铜的胸径为时,树高为 .(1)、求与之间的函数表达式;(2)、当这种树的胸径为时,其树高是多少?23. 某校数学兴趣小组的同学们从“校园农场“中随机抽取了棵西红柿植株,并统计了每棵植株上小西红柿的个数其数据如下: , , , , , , , , , , , , , , , , , , , 通过对以上数据的分析整理,绘制了统计图表:分组
频数
组内小西红柿的总个数
根据以上信息,解答下列问题:
(1)、补全频数分布直方图:这个数据的众数是 ▲ ;(2)、求这个数据的平均数;(3)、“校园农场“中共有棵这种西红柿植株,请估计这棵西红柿植株上小西缸柿的总个数.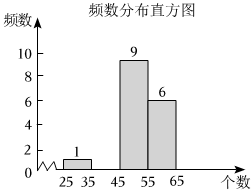 24. 如图,内接于 , , 过点作的垂线,交于点 , 并与的延长线交于点 , 作 , 垂足为 , 交于点 .
24. 如图,内接于 , , 过点作的垂线,交于点 , 并与的延长线交于点 , 作 , 垂足为 , 交于点 . (1)、求证:;(2)、若的半径 , , 求线段的长.25. 某校想将新建图书楼的正门设计为一个抛物线型门,并要求所设计的拱门的跨度与拱高之积为 , 还要兼顾美观、大方,和谐、通畅等因素,设计部门按要求价出了两个设计方案现把这两个方案中的拱门图形放入平面直角坐标系中,如图所示:
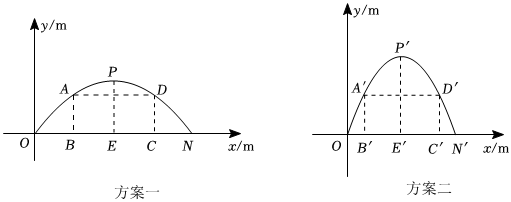
(1)、求证:;(2)、若的半径 , , 求线段的长.25. 某校想将新建图书楼的正门设计为一个抛物线型门,并要求所设计的拱门的跨度与拱高之积为 , 还要兼顾美观、大方,和谐、通畅等因素,设计部门按要求价出了两个设计方案现把这两个方案中的拱门图形放入平面直角坐标系中,如图所示:方案一,抛物线型拱门的跨度 , 拱高其中,点在轴上, , .
方案二,抛物线型拱门的跨度 , 拱高其中,点在轴上, , .
要在拱门中设置高为的矩形框架,其面积越大越好框架的粗细忽略不计方案一中,矩形框架的面积记为 , 点、在抛物线上,边在上;方案二中,矩形框架的面积记为 , 点 , 在抛物线上,边在上现知,小华已正确求出方案二中,当时, , 请你根据以上提供的相关信息,解答下列问题:
 (1)、求方案一中抛物线的函数表达式;(2)、在方案一中,当时,求矩形框架的面积并比较 , 的大小.26.
(1)、求方案一中抛物线的函数表达式;(2)、在方案一中,当时,求矩形框架的面积并比较 , 的大小.26. (1)、如图 , 在中, , , 若的半径为 , 点在上,点在上,连接 , 求线段的最小值;(2)、如图所示,五边形是某市工业新区的外环路,新区管委会在点处,点处是该市的一个交通枢纽已知: , , 根据新区的自然环境及实际需求,现要在矩形区域内含边界修一个半径为的圆型环道;过圆心 , 作 , 垂足为 , 与交于点连接 , 点在上,连接其中,线段、及是要修的三条道路,要在所修迅路、之和最短的情况下,使所修道路最短,试求此时环道的圆心到的距离的长.
(1)、如图 , 在中, , , 若的半径为 , 点在上,点在上,连接 , 求线段的最小值;(2)、如图所示,五边形是某市工业新区的外环路,新区管委会在点处,点处是该市的一个交通枢纽已知: , , 根据新区的自然环境及实际需求,现要在矩形区域内含边界修一个半径为的圆型环道;过圆心 , 作 , 垂足为 , 与交于点连接 , 点在上,连接其中,线段、及是要修的三条道路,要在所修迅路、之和最短的情况下,使所修道路最短,试求此时环道的圆心到的距离的长.