广东省2023年中考数学试卷
试卷更新日期:2023-06-29 类型:中考真卷
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 负数的概念最早出现在我国古代著名的数学专著《九章算术》中,如果把收入5元记作+5元,那么支出5元记作( )A、元 B、0元 C、元 D、元2. 下列出版社的商标图案中,是轴对称图形的为 ( )A、
 B、
B、 C、
C、 D、
D、 3. 2023年5月28日,我国自主研发的C919国产大飞机商业首航取得圆满成功,C919可储存约186000升燃油,将数据186000用科学记数法表示为 ( )A、 B、 C、 D、4. 如图,街道与平行,拐角 , 则拐角 ( )
3. 2023年5月28日,我国自主研发的C919国产大飞机商业首航取得圆满成功,C919可储存约186000升燃油,将数据186000用科学记数法表示为 ( )A、 B、 C、 D、4. 如图,街道与平行,拐角 , 则拐角 ( )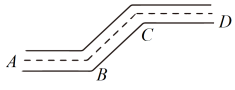 A、 B、 C、 D、5. 计算的结果为 ( )A、 B、 C、 D、6. 我国著名数学家华罗庚曾为普及优选法作出重要贡献,优选法中有一种0.618法应用了( )A、黄金分割数 B、平均数 C、众数 D、中位数7. 某学校开设了劳动教育课程.小明从感兴趣的“种植”“烹饪”“陶艺”“木工”4门课程中随机选择一门学习,每门课程被选中的可能性相等,小明恰好选中“烹饪”的概率为 ( )A、 B、 C、 D、8. 一元一次不等式组的解集为 ( )A、 B、 C、 D、9. 如图,是的直径, , 则( )
A、 B、 C、 D、5. 计算的结果为 ( )A、 B、 C、 D、6. 我国著名数学家华罗庚曾为普及优选法作出重要贡献,优选法中有一种0.618法应用了( )A、黄金分割数 B、平均数 C、众数 D、中位数7. 某学校开设了劳动教育课程.小明从感兴趣的“种植”“烹饪”“陶艺”“木工”4门课程中随机选择一门学习,每门课程被选中的可能性相等,小明恰好选中“烹饪”的概率为 ( )A、 B、 C、 D、8. 一元一次不等式组的解集为 ( )A、 B、 C、 D、9. 如图,是的直径, , 则( ) A、 B、 C、 D、10. 如图,抛物线经过正方形的三个顶点A,B,C,点B在轴上,则的值为( )
A、 B、 C、 D、10. 如图,抛物线经过正方形的三个顶点A,B,C,点B在轴上,则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本大题共5小题,每小题3分,共15分.
-
11. 因式分解: .12. 计算 .13. 某蓄电池的电压为 , 使用此蓄电池时,电流(单位:)与电阻(单位:)的函数表达式为 , 当时,的值为 .14. 某商品进价4元,标价5元出售,商家准备打折销售,但其利润率不能少于10%,则最多可打折.15. 边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为 .

三、解答题(一):本大题共3小题,第16题10分,第17、18题各7分,共24分.
-
16.(1)、计算:;(2)、已知一次函数的图象经过点与点 , 求该一次函数的表达式.17. 某学校开展了社会实践活动,活动地点距离学校12km,甲、乙两同学骑自行车同时从学校出发,甲的速度是乙的1.2倍,结果甲比乙早到10min,求乙同学骑自行车的速度.18. 2023年5月30日,神舟十六号载人飞船发射取得圆满成功,3名航天员顺利进驻中国空间站,如图中的照片展示了中国空间站上机械臂的一种工作状态,当两臂 , 两臂夹角时,求A,B两点间的距离.(结果精确到 , 参考数据 , , )

四、解答题(二):本大题共3小题,每小题9分,共27分.
-
19. 如图,在中, .
 (1)、实践与操作:用尺规作图法过点作边上的高;(保留作图痕迹,不要求写作法)(2)、应用与计算:在(1)的条件下, , , 求的长.20. 综合与实践
(1)、实践与操作:用尺规作图法过点作边上的高;(保留作图痕迹,不要求写作法)(2)、应用与计算:在(1)的条件下, , , 求的长.20. 综合与实践主题:制作无盖正方体形纸盒
素材:一张正方形纸板.
步骤1:如图1,将正方形纸板的边长三等分,画出九个相同的小正方形,并剪去四个角上的小正方形;
步骤2:如图2,把剪好的纸板折成无盖正方体形纸盒.
猜想与证明:
 (1)、直接写出纸板上与纸盒上的大小关系;(2)、证明(1)中你发现的结论.21. 小红家到学校有两条公共汽车线路,为了解两条线路的乘车所用时间,小红做了试验,第一周(5个工作日)选择A线路,第二周(5个工作日)选择B线路,每天在固定时间段内乘车2次并分别记录所用时间,数据统计如下:(单位:min)
(1)、直接写出纸板上与纸盒上的大小关系;(2)、证明(1)中你发现的结论.21. 小红家到学校有两条公共汽车线路,为了解两条线路的乘车所用时间,小红做了试验,第一周(5个工作日)选择A线路,第二周(5个工作日)选择B线路,每天在固定时间段内乘车2次并分别记录所用时间,数据统计如下:(单位:min)数据统计表
试验序号 1 2 3 4 5 6 7 8 9 10 A线路所用时间 15 32 15 16 34 18 21 14 35 20 B线路所用时间 25 29 23 25 27 26 31 28 30 24 数据折线统计图
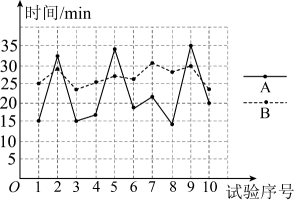
根据以上信息解答下列问题:
平均数
中位数
众数
方差
A线路所用时间
22
a
15
63.2
B线路所用时间
b
26.5
c
6.36
(1)、填空:;;;(2)、应用你所学的统计知识,帮助小红分析如何选择乘车线路.五、解答题(三):本大题共2小题,每小题12分,共24分.
-
22. 综合探究
如图1,在矩形中 , 对角线相交于点 , 点关于的对称点为 , 连接交于点 , 连接 .
 (1)、求证:;(2)、以点为圆心,为半径作圆.
(1)、求证:;(2)、以点为圆心,为半径作圆.①如图2,与相切,求证:;
②如图3,与相切, , 求的面积.
23. 综合运用如图1,在平面直角坐标系中,正方形的顶点A在轴的正半轴上,如图2,将正方形绕点逆时针旋转,旋转角为 , 交直线于点 , 交轴于点 .
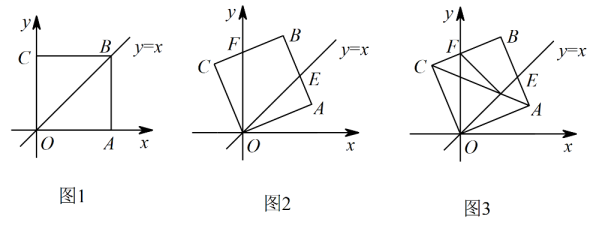 (1)、当旋转角为多少度时,;(直接写出结果,不要求写解答过程)(2)、若点 , 求的长;(3)、如图3,对角线交轴于点 , 交直线于点 , 连接 , 将与的面积分别记为与 , 设 , , 求关于的函数表达式.
(1)、当旋转角为多少度时,;(直接写出结果,不要求写解答过程)(2)、若点 , 求的长;(3)、如图3,对角线交轴于点 , 交直线于点 , 连接 , 将与的面积分别记为与 , 设 , , 求关于的函数表达式.