（苏科版）2023-2024学年七年级上学期微专题提分精炼——数学思想

试卷更新日期：2023-06-29 类型：复习试卷

进入出卷网下载

一、选择题

1. 幻方是古老的数学问题，我国古代的《洛书》中记载了最早的幻方--九宫图．请同学们在数字1，2，3，4，5，6，7，8，9中选择合适的数字填入如图所示的幻方中，要求每一横行、同一竖行、两条斜对角线上的数字之和都是15，则n的值为（）

7
2
n
5

A、1 B、2 C、8 D、9

查看试题解析
2. 身份证号码告诉我们很多信息，某人的身份证号码是130503196704010012，其中13、05、03是此人所属的省(市、自治区)、市、县(市、区)的编码，1967、04、01是此人出生的年、月、日，071是顺序码，2为校验码：那么身份证号码是321084198101208022的人的生日是（）

A、8月10日 B、10月12日 C、1月20日 D、12月8日

查看试题解析
3. 一个长26厘米、宽19厘米、高0.7厘米的物体，最有可能是（）

A、衣柜 B、数学课本 C、手机 D、橡皮

查看试题解析
4. 直径为60厘米的圆，在生活中可能是（）

A、杯盖的面 B、井盖的面 C、一元硬币的面 D、蒙古包占地的面

查看试题解析
5. 在解决下面三个问题时，运用转化策略的是（）
①计算5÷ $\frac{5}{6}$ 时，可以这样算：5÷ $\frac{5}{6}$ ＝5× $\frac{6}{5}$ ；②探究圆的面积；③求三角形的内角和．

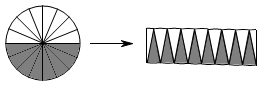A、只有①② B、只有①③ C、只有②③ D、①②③都是

查看试题解析
6. 拿一个4倍的放大镜看一个1°的角，则这个角为（）

A、4 B、1 C、5 D、不能确定，视放大镜的距离而定

查看试题解析
7. 中国人对方程的研究有悠久的历史．中国古代数学著作《九章算术》中有专门以“方程”命名的一章．中国古代数学家表示方程时，只用算筹表示各未知数的系数，而没有使用专门的记法来表示未知数.1859年中国清代一位数学家在翻译外国数学著作时，开始将equation（指含未知数的等式）一词译为“方程”，至今一直这样沿用，这位清代数学家是（）

A、花拉子米 B、李治 C、李善兰 D、刘徽

查看试题解析
8. 我们这样研究一个数的绝对值的性质：当a＞0时，如|a|=|2|=2，此时a的绝对值是它本身；当a=0时，如|a|=0，此时a的绝对值是0；当a＜0时，如|a|=|﹣2|=2，此时a的绝对值是它的相反数．这种分析问题的方法所体现的数学思想是（）

A、分类讨论思想 B、公理化思想 C、数形结合思想 D、转化思想

查看试题解析
9. 估计2⁸cm接近于（）

A、七年级数学课本的厚度 B、姚明的身高 C、六层教学楼的高度 D、长白山主峰的高度

查看试题解析
10. 在下面四个问题的解决过程中都运用了什么策略？（）

⑴用如图①所示的方法推导三角形面积的计算过程；

⑵计算 $6 \div \frac{2}{3}$ 时，可以这样算： $6 \div \frac{2}{3} = 6 \times \frac{3}{2}$ ；

⑶用如图②所示的方法推导圆的面积计算公式的过程；

⑷计算 $2.5 \times 1.7$ 时，先看 $25 \times 17$ ，再在积中添上小数点儿．

A、列表 B、列举 C、转化 D、倒推

查看试题解析

二、填空题

11. 数轴上一点A，一只蚂蚁从A点出发爬了5个单位长度到达了原点，则点A所表示的数是.

查看试题解析
12. 若│a│=3,b是绝对值最小的数,c是最大的负整数,则 $a^{2} + b - c$ 的值为．

查看试题解析
13. 在我们学习的数中，有这样一个数：它是绝对值最小的数．则这个数是．

查看试题解析
14. 已知a是最大的负整数，b是最小的正整数，c是绝对值最小的数，则(a＋c)÷b＝.

查看试题解析
15. 已知，在同一平面内，∠AOB=30°，射线OC在∠AOB的外部，OD平方∠AOC，若∠BOD=40°，则∠AOC的度数为

查看试题解析

三、解答题

16. 若a，b互为相反数，c，d互为倒数， $m^{2} = 1$ ，n是绝对值最小的有理数，求 $\frac{2 {(a + b)}^{2015} - {(- c d)}^{2017} - \frac{b}{a}}{m + n}$ 的值.

查看试题解析
17. 先阅读下面例题的解题过程，再解答后面的题目.
例：已知代数式 $9 - 6 y - 4 y^{2} = 7$ ，求 $2 y^{2} + 3 y + 7$ 的值.

解：由 $9 - 6 y - 4 y^{2} = 7$ ，得 $- 6 y - 4 y^{2} = 7 - 9$ ，即 $6 y + 4 y^{2} = 2$ ，

因此 $3 y + 2 y^{2} = 1$ ，所以 $2 y^{2} + 3 y + 7$ =8

题目：已知代数式 $14 x + 5 - 21 x^{2}$ 的值是－2，求 $6 x^{2} - 4 x + 5$ 的值.

查看试题解析
18. 12人乘车去某地，可供租的车辆有两种：一种车可乘8人，另一种车可乘4人．
（1）请给出3种以上的租车方案；
（2）如果第一种车的租金是300元/天，第二种车的租金是200元/天，那么采用哪种方案费用最少？

查看试题解析
19. 请认真观察你的房间（或室外某一广场）的地面是由多少块正方形（或长方形）的地板砖铺成的，你能用比较简单的方法，估测出整个房间（或广场）的面积吗？每一块地板砖的面积是整个房间（或广场）面积的几分之几？（结果用科学记数法表示）

查看试题解析

四、综合题

20. 阅读材料：我们知道，4x-2x+x＝（4-2+1）x＝3x，类似地，我们把（a+b）看成一个整体，则4（a+b）-2（a+b）+（a+b）＝（4-2+1）（a+b）＝3（a+b）．“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．尝试应用整体思想解决下列问题：

(1)、把（a-b）²看成一个整体，合并2（a-b）²-6（a-b）²+3（a-b）²；

(2)、已知x²-2y＝4，求6x²-12y-27的值；

(3)、已知a-2b＝3，2b-c＝-5，c-d＝10，求（a-c）+（2b-d）-（2b-c）的值．

查看试题解析
21. 仔细观察下面的正四面体、正六面体、正八面体，解决下列问题：

(1)、填空：
①正四面体的顶点数V＝  ▲   ，面数F＝  ▲   ，棱数E＝  ▲  .
②正六面体的顶点数V＝  ▲   ，面数F＝  ▲   ，棱数E＝  ▲  .
③正八面体的顶点数V＝  ▲   ，面数F＝  ▲   ，棱数E＝  ▲

(2)、若将多面体的顶点数用V表示，面数用F表示，棱数用E表示，则V、F、E之间的数量关系可用一个公式来表示，这就是著名的欧拉公式，请写出欧拉公式：

(3)、如果一个多面体的棱数为30，顶点数为20，那么它有多少个面？

查看试题解析
22. 如图，A、B、C是数轴上的三点，O是原点，BO=3，AB=2BO，5AO=3CO．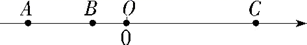

(1)、写出数轴上点A、C表示的数；

(2)、点P、Q分别从A、C同时出发，点P以每秒2个单位长度的速度沿数轴向右匀速运动，点Q以每秒6个单位长度的速度沿数轴向左匀速运动，M为线段AP的中点，点N在线段CQ上，且CN= $\frac{2}{3}$ CQ．设运动的时间为t（t>0）秒．
①求数轴上点M、N表示的数（用含t的式子表示）；

②t为何值时，M、N两点到原点的距离相等?

查看试题解析
23. 如图，直角三角板的直角顶点O在直线AB上，OC，OD是三角板的两条直角边，OE平分∠AOD．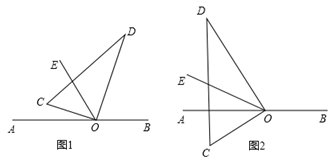

(1)、如图1，若∠COE=20°，则∠BOD=；若∠COE=α，则∠BOD=（用含α的代数式表示）；

(2)、将图1中三角板绕O逆时针旋转到图2的位置时，试猜测∠COE与∠BOD之间有怎样的数量关系，并说明理由．

查看试题解析