(苏科版)2023-2024学年八年级上学期微专题提分精炼——等腰三角形与等边三角形
试卷更新日期:2023-06-29 类型:复习试卷
一、选择题
-
1. 如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于E点,DF⊥AC于点F,则下列四个结论:①AD上任意一点到AB,AC两边的距离相等; ②AD⊥BC且BD=CD;③∠BDE=∠CDF;④AE=AF.其中正确的有( )
 A、②③ B、①③ C、①②④ D、①②③④2. 如图, 在中, , , 与相交于点 , 于.则下列数量关系正确的为( )
A、②③ B、①③ C、①②④ D、①②③④2. 如图, 在中, , , 与相交于点 , 于.则下列数量关系正确的为( ) A、 B、 C、 D、3. 如图,在等腰三角形中,是底边上的中线,是高线.图中与一定相等的角有(不含本身)( )
A、 B、 C、 D、3. 如图,在等腰三角形中,是底边上的中线,是高线.图中与一定相等的角有(不含本身)( ) A、1个 B、2个 C、3个 D、4个4. 如图,在△ABC中,AB=AC=10,BC=12,AD平分∠BAC,则AD等于( )
A、1个 B、2个 C、3个 D、4个4. 如图,在△ABC中,AB=AC=10,BC=12,AD平分∠BAC,则AD等于( ) A、6 B、7 C、8 D、95. 如图,边长为a的等边△ABC中,BF是AC上中线且BF=b,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,则△AEF周长的最小值是( )
A、6 B、7 C、8 D、95. 如图,边长为a的等边△ABC中,BF是AC上中线且BF=b,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,则△AEF周长的最小值是( ) A、 B、 C、a+b D、a6. 如图,在中, , , D为BC上一点, , 则BC的长为( )
A、 B、 C、a+b D、a6. 如图,在中, , , D为BC上一点, , 则BC的长为( ) A、10 B、12 C、14 D、167. 如图,在中, , , 分别是边 , 上的点, , CD与BE交于点F,则图中全等三角形的对数为( )
A、10 B、12 C、14 D、167. 如图,在中, , , 分别是边 , 上的点, , CD与BE交于点F,则图中全等三角形的对数为( ) A、2 B、3 C、4 D、58. 如图,在中, , AD是角平分线,且 , , 点E为中点,则的值为( )
A、2 B、3 C、4 D、58. 如图,在中, , AD是角平分线,且 , , 点E为中点,则的值为( ) A、5 B、5.8 C、6 D、6.59. 如图,以直角三角形的各边边长分别向外做等边三角形,再把较小的两个三角形按如图2的方式放置在最大的三角形内,是小梯形面积,是三个三角形重叠部分的面积,是大梯形的面积,是平行四边形的面积,则下列关系一定成立的是( )
A、5 B、5.8 C、6 D、6.59. 如图,以直角三角形的各边边长分别向外做等边三角形,再把较小的两个三角形按如图2的方式放置在最大的三角形内,是小梯形面积,是三个三角形重叠部分的面积,是大梯形的面积,是平行四边形的面积,则下列关系一定成立的是( ) A、 B、 C、 D、10. 如图, , , 记 , , 当时,α与β之间的数量关系为( )
A、 B、 C、 D、10. 如图, , , 记 , , 当时,α与β之间的数量关系为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 等腰中, , 顶角A为 , 平面内有一点P,满足且 , 则的度数为 .12. 如图,直线与x轴,y轴分别交于A,C两点,点B与点A关于y轴对称,连接 , , 点M,N分别是线段上的动点(M不与A,B重合),且满足.当为等腰三角形时,M的坐标为.
 13. 如图,等边三角形 , , 点D,E,F分别是 , , 的中点,点P是线段上的一动点,连接 , , 则周长的最小值是.
13. 如图,等边三角形 , , 点D,E,F分别是 , , 的中点,点P是线段上的一动点,连接 , , 则周长的最小值是. 14. 如图,在中, , , , D为的中点,P为上一动点,连接 , , 则的最小值是.
14. 如图,在中, , , , D为的中点,P为上一动点,连接 , , 则的最小值是.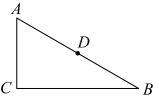 15. 已知等腰 , 的相邻外角为 , 则这个三角形的顶角为.
15. 已知等腰 , 的相邻外角为 , 则这个三角形的顶角为.三、解答题
-
16. 如图,已知是的一个外角,平分 , 且 , 求证:为等腰三角形.
 17. 如图,在中, , , 于点D,于点E, , 求的长.
17. 如图,在中, , , 于点D,于点E, , 求的长.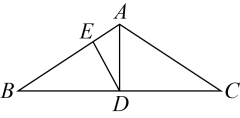 18. 如图,在△ABC中,AB=AC,AD⊥BC,∠BAD=28°,且AD=AE,求∠EDC的度数.
18. 如图,在△ABC中,AB=AC,AD⊥BC,∠BAD=28°,且AD=AE,求∠EDC的度数. 19. △ABC中,AB=AC,E为AC中点,F为BE上一点,且CE=CF.若△ABC的三条边长均为偶数,且BF与BE两条线段长度的乘积为20. 求△ABC的周长.
19. △ABC中,AB=AC,E为AC中点,F为BE上一点,且CE=CF.若△ABC的三条边长均为偶数,且BF与BE两条线段长度的乘积为20. 求△ABC的周长.
四、综合题
-
20. 如图,在平行四边形ABCD中,点E、F为对角线BD的三等分点,连结AE,CF,AF,CE.
 (1)、求证:四边形AECF为平行四边形;(2)、若四边形AECF为菱形,且AE=BE,求BAD的度数.21. 在中, , 点E在边上,连结 , 将沿翻折使得点D落在边上得 , 连结 .
(1)、求证:四边形AECF为平行四边形;(2)、若四边形AECF为菱形,且AE=BE,求BAD的度数.21. 在中, , 点E在边上,连结 , 将沿翻折使得点D落在边上得 , 连结 . (1)、如图1, , , 求的度数.(2)、如图2,若 , , 求的度数.22. 如图,在中,的垂直平分线交于点 , 交于点 , 于 , .
(1)、如图1, , , 求的度数.(2)、如图2,若 , , 求的度数.22. 如图,在中,的垂直平分线交于点 , 交于点 , 于 , . (1)、求证:为线段的中点.(2)、若 , 求的度数.23. 定义:三角形一边上的点到三角形的另两条边的距离相等,称此点为这个三角形这边上的雅实心,如:
(1)、求证:为线段的中点.(2)、若 , 求的度数.23. 定义:三角形一边上的点到三角形的另两条边的距离相等,称此点为这个三角形这边上的雅实心,如:如图1,当点P在的边上时,若于点D,于点E,且 , 则称点P为的边上的雅实心,各边上的三个雅实心为顶点构成新三角形,叫做的雅实三角形.
 (1)、如图2,中, , , 求边上的雅实心P到的距离.(2)、如图3,等边的边长为 , 求等边的雅实三角形的面积.(3)、如图4,在平面直角坐标系中,点A,B分别在x,y轴上,且 , , 求的斜边上的雅实心P的坐标.
(1)、如图2,中, , , 求边上的雅实心P到的距离.(2)、如图3,等边的边长为 , 求等边的雅实三角形的面积.(3)、如图4,在平面直角坐标系中,点A,B分别在x,y轴上,且 , , 求的斜边上的雅实心P的坐标.