(苏科版)2023-2024学年八年级上学期微专题提分精炼——角平分线与线段垂直平分线
试卷更新日期:2023-06-29 类型:复习试卷
一、选择题
-
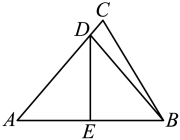
1. 如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于E点,DF⊥AC于点F,则下列四个结论:①AD上任意一点到AB,AC两边的距离相等; ②AD⊥BC且BD=CD;③∠BDE=∠CDF;④AE=AF.其中正确的有( )
 A、②③ B、①③ C、①②④ D、①②③④2. 如图,中,是高, , 则长为( )
A、②③ B、①③ C、①②④ D、①②③④2. 如图,中,是高, , 则长为( ) A、4 B、5 C、6 D、73. 如图,在中,分别以点A,B为圆心,大于长为半径画弧,两弧相交于点E,F,连接 , 作直线交于点M,连接 , 则下列判断不正确的是( )
A、4 B、5 C、6 D、73. 如图,在中,分别以点A,B为圆心,大于长为半径画弧,两弧相交于点E,F,连接 , 作直线交于点M,连接 , 则下列判断不正确的是( ) A、 B、 C、 D、4. 如图,在中, , , 平分 , , 为边的垂直平分线且分别交、于点、 , 若 , , 则的长是( )
A、 B、 C、 D、4. 如图,在中, , , 平分 , , 为边的垂直平分线且分别交、于点、 , 若 , , 则的长是( )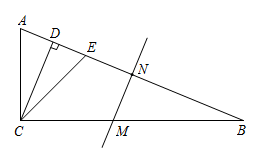 A、2 B、 C、 D、5. 如图,在中, , 分别以A,C为圆心,大于长为半径作弧,两弧相交于点M,N,作直线 , 与 , 分别交于D,E,连接 , 若 , , 则的周长为( )
A、2 B、 C、 D、5. 如图,在中, , 分别以A,C为圆心,大于长为半径作弧,两弧相交于点M,N,作直线 , 与 , 分别交于D,E,连接 , 若 , , 则的周长为( ) A、16 B、17 C、18 D、196. 如图,在等腰三角形ABC中,AB=AC=4,∠BAC=30°,AG是底边BC上的高.在AG的延长线上有一个动点D,连接CD,作∠CDE=150°,交AB的延长线于点E,∠CDE的角平分线交AB边于点F,则在点D运动的过程中,线段EF的最小值( )
A、16 B、17 C、18 D、196. 如图,在等腰三角形ABC中,AB=AC=4,∠BAC=30°,AG是底边BC上的高.在AG的延长线上有一个动点D,连接CD,作∠CDE=150°,交AB的延长线于点E,∠CDE的角平分线交AB边于点F,则在点D运动的过程中,线段EF的最小值( ) A、6 B、4 C、3 D、27. 如图,△ABC中,AB<AC<BC,如果要使用尺规作图的方法在BC上确定一点P,使PA+PB=BC,那么符合要求的作图痕迹是( )A、
A、6 B、4 C、3 D、27. 如图,△ABC中,AB<AC<BC,如果要使用尺规作图的方法在BC上确定一点P,使PA+PB=BC,那么符合要求的作图痕迹是( )A、 B、
B、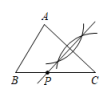 C、
C、 D、
D、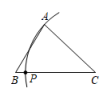 8. 如图,在中, , 以顶点为圆心,适当长为半径画弧,分别交边、于点、 , 再分别以点、为圆心,大于的长为半径画弧,两弧交于点 , 作射线交边于点 , 若 , , 则的面积是( )
8. 如图,在中, , 以顶点为圆心,适当长为半径画弧,分别交边、于点、 , 再分别以点、为圆心,大于的长为半径画弧,两弧交于点 , 作射线交边于点 , 若 , , 则的面积是( )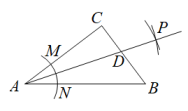 A、15 B、30 C、45 D、609. 如图,长方形纸片中, 点是的中点,连接; 按以下步骤作图:①分别 以点和为圆心, 以大于的等长为半径作弧,两弧相交于点和;②作直线 , 且直线刚好经过点.若 , 则的长度是( )
A、15 B、30 C、45 D、609. 如图,长方形纸片中, 点是的中点,连接; 按以下步骤作图:①分别 以点和为圆心, 以大于的等长为半径作弧,两弧相交于点和;②作直线 , 且直线刚好经过点.若 , 则的长度是( ) A、2 B、 C、 D、410. 如图,为的角平分线, , 过作于 , 交的延长线于 , 则下列结论:
A、2 B、 C、 D、410. 如图,为的角平分线, , 过作于 , 交的延长线于 , 则下列结论:①;②;③;④ .
其中正确结论的序号有( )
 A、①②③④ B、②③④ C、①②③ D、①②④
A、①②③④ B、②③④ C、①②③ D、①②④二、填空题
-
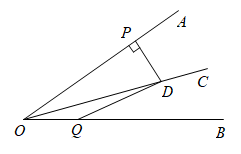
11. 如图,射线是的角平分线,是射线上一点,于点 , , 若点是射线上一点, , 则的面积是.
 12. 如图,在中,AB=AC,BC=4,面积是10.AB的垂直平分线ED分别交AC,AB边于E、D两点,若点F为BC边的中点,点P为线段ED上一动点,则PBF周长的最小值为.
12. 如图,在中,AB=AC,BC=4,面积是10.AB的垂直平分线ED分别交AC,AB边于E、D两点,若点F为BC边的中点,点P为线段ED上一动点,则PBF周长的最小值为.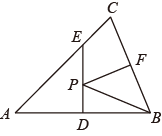 13. 如图所示,在边长为2的等边中,点为的中点,点为的中点,过点作交于点 , 交于点 , 点是线段上一个动点,连接 , , 则的周长的最小值是.
13. 如图所示,在边长为2的等边中,点为的中点,点为的中点,过点作交于点 , 交于点 , 点是线段上一个动点,连接 , , 则的周长的最小值是. 14. 如图,在中,是边上的高,平分 , 交于点E, , 若的面积为9,则的长为.
14. 如图,在中,是边上的高,平分 , 交于点E, , 若的面积为9,则的长为. 15. 如图,在Rt△ABC中,AC=4,AB=5,∠C=90°,BD平分∠ABC交AC于点D,则BD的长是.
15. 如图,在Rt△ABC中,AC=4,AB=5,∠C=90°,BD平分∠ABC交AC于点D,则BD的长是.
三、解答题
-
16. 如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC,垂足分别是E,F,连接EF,EF与BD相交于点P.求证:EP=FP.
 17. 如图,在△ABC中,AB=AC,CE=6,直线ED是线段AC的垂直平分线,∠BAC=120°,求线段BE的长.
17. 如图,在△ABC中,AB=AC,CE=6,直线ED是线段AC的垂直平分线,∠BAC=120°,求线段BE的长.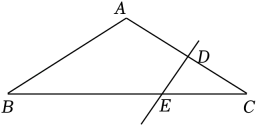 18. 如图,在中, , 是的垂直平分线,交于点E.已知的周长是24,的长是5.求的周长.
18. 如图,在中, , 是的垂直平分线,交于点E.已知的周长是24,的长是5.求的周长. 19. 如图,在中,的垂直平分线交于点E,交于点F,点D为的中点,连接 , 此时 , . 求证: .
19. 如图,在中,的垂直平分线交于点E,交于点F,点D为的中点,连接 , 此时 , . 求证: .
四、综合题
-
20. 如图,在中,的垂直平分线交于点 , 交于点 , 于 , .
 (1)、求证:为线段的中点.(2)、若 , 求的度数.
(1)、求证:为线段的中点.(2)、若 , 求的度数.