(苏科版)2023-2024学年八年级上学期微专题提分精炼——轴对称的性质
试卷更新日期:2023-06-29 类型:复习试卷
一、选择题
-
1. 把各顶点的横坐标都乘以-1,纵坐标都不变,所得图形是下列答案中的( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,在长方形纸片ABCD中,AB=8cm,AD=6cm.把长方形纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,则AF的长为( )
2. 如图,在长方形纸片ABCD中,AB=8cm,AD=6cm.把长方形纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,则AF的长为( ) A、 cm B、 cm C、7cm D、 cm3. 欧几里得在《几何原本》中,记载了用图解法解方程的方法,类似地我们可以用折纸的方法求方程的一个正根.如图,一张边长为1的正方形的纸片ABCD,先折出AD、BC的中点G、H,再折出线段AN,然后通过沿线段AN折叠使AD落在线段AH上,得到点D的新位置P,并连接NP、NH,此时,在下列四个选项中,有一条线段的长度恰好是方程的一个正根,则这条线段是( )
A、 cm B、 cm C、7cm D、 cm3. 欧几里得在《几何原本》中,记载了用图解法解方程的方法,类似地我们可以用折纸的方法求方程的一个正根.如图,一张边长为1的正方形的纸片ABCD,先折出AD、BC的中点G、H,再折出线段AN,然后通过沿线段AN折叠使AD落在线段AH上,得到点D的新位置P,并连接NP、NH,此时,在下列四个选项中,有一条线段的长度恰好是方程的一个正根,则这条线段是( ) A、线段BH B、线段CN C、线段DN D、线段NH4. 如图,将沿着平行于的直线折叠,得到 , 若 , 则的度数是( )
A、线段BH B、线段CN C、线段DN D、线段NH4. 如图,将沿着平行于的直线折叠,得到 , 若 , 则的度数是( ) A、 B、 C、 D、5. 如图,长方形纸片ABCD中,AD=4,AB=10,按如图的方式折叠,使点B与点D重合,折痕为EF,则DE长为( )
A、 B、 C、 D、5. 如图,长方形纸片ABCD中,AD=4,AB=10,按如图的方式折叠,使点B与点D重合,折痕为EF,则DE长为( ) A、4.8 B、5 C、5.8 D、66. 如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标( )
A、4.8 B、5 C、5.8 D、66. 如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标( ) A、(4,10) B、(10,6) C、(10,4) D、(10,3)7. 如图所示,以 的顶点 O 为圆心,适当长为半径画弧,交 于点 C,交 于点 D,再分别以点 C 、 D 为圆心,大于 长为半径画弧,两弧在 内部交于点 E,过点 E 作射线 , 连接则下列说法错误的( )
A、(4,10) B、(10,6) C、(10,4) D、(10,3)7. 如图所示,以 的顶点 O 为圆心,适当长为半径画弧,交 于点 C,交 于点 D,再分别以点 C 、 D 为圆心,大于 长为半径画弧,两弧在 内部交于点 E,过点 E 作射线 , 连接则下列说法错误的( ) A、射线 是 的平分线 B、 是等腰三角形 C、C、D 两点关于 所在直线对称 D、O、E 两点关于 所在直线对称8. 如图,在四边形中, , , 、分别是、上的点,将沿着翻折,得到 , 若ME//AD,EN//DC,则的度数为( )
A、射线 是 的平分线 B、 是等腰三角形 C、C、D 两点关于 所在直线对称 D、O、E 两点关于 所在直线对称8. 如图,在四边形中, , , 、分别是、上的点,将沿着翻折,得到 , 若ME//AD,EN//DC,则的度数为( ) A、 B、 C、 D、9. 如图,在的正方形的网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的为格点三角形,在图中最多能画出( )个格点三角形与成轴对称.
A、 B、 C、 D、9. 如图,在的正方形的网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的为格点三角形,在图中最多能画出( )个格点三角形与成轴对称. A、6 B、5 C、4 D、310. 有一直角三角形纸片,∠C=90°BC=6,AC=8,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长为( )
A、6 B、5 C、4 D、310. 有一直角三角形纸片,∠C=90°BC=6,AC=8,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长为( )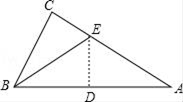 A、 B、 C、 D、4
A、 B、 C、 D、4二、填空题
-
11. 如图,在平行四边形ABCD中,E是边CD上一点,将ADE沿AE折叠至AD′E处,AD′与CE交于点F,若B=53°,DAE=20°,则FED′的度数为 .
 12. 如图,直线与x轴,y轴分别交于A,C两点,点B与点A关于y轴对称,连接 , , 点M,N分别是线段上的动点(M不与A,B重合),且满足.当为等腰三角形时,M的坐标为.
12. 如图,直线与x轴,y轴分别交于A,C两点,点B与点A关于y轴对称,连接 , , 点M,N分别是线段上的动点(M不与A,B重合),且满足.当为等腰三角形时,M的坐标为. 13. 如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若∠C=45°,∠B=30°,AD=2,则AB2-AC2的值是 .
13. 如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若∠C=45°,∠B=30°,AD=2,则AB2-AC2的值是 . 14. 如图,在长方形纸片中, , , 点M为上一点,将沿翻至 , 交于点G,交于点F,且 , 则的长度是.
14. 如图,在长方形纸片中, , , 点M为上一点,将沿翻至 , 交于点G,交于点F,且 , 则的长度是.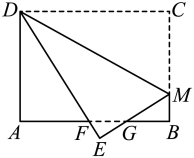 15. 如图1,小明将一张长方形纸片对折,使长方形两边重合,折痕为EF,铺开后沿BC折叠,使点A与EF上的点D重合.如图2,再将该长方形纸片进行折叠,折痕分别为HG,KL,使长方形的两边均与EF重合;铺开后沿BP折叠,使点A与KL上的点Q重合;分别连结图1中的AD与图2中的AQ,则的值为.
15. 如图1,小明将一张长方形纸片对折,使长方形两边重合,折痕为EF,铺开后沿BC折叠,使点A与EF上的点D重合.如图2,再将该长方形纸片进行折叠,折痕分别为HG,KL,使长方形的两边均与EF重合;铺开后沿BP折叠,使点A与KL上的点Q重合;分别连结图1中的AD与图2中的AQ,则的值为.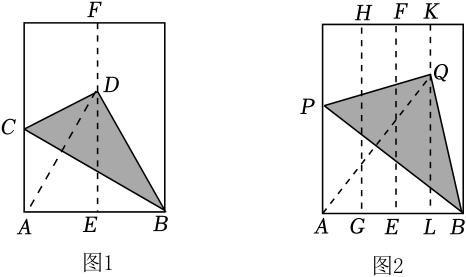
三、解答题
-
16. 如图,长方形纸片ABCD沿对角线AC折叠,设点D落在D′处,BC交AD′于点E,AB=6cm,BC=8cm,求阴影部分的面积.
 17. 如图所示,在矩形中, , , 若将矩形沿折叠,使点落在边上的点处,则线段的长?
17. 如图所示,在矩形中, , , 若将矩形沿折叠,使点落在边上的点处,则线段的长? 18. 如图,在中, , 将沿着直线折叠,点落在点的位置,求的度数.
18. 如图,在中, , 将沿着直线折叠,点落在点的位置,求的度数. 19. 如图,在 中, , , ,将 沿AD折叠,使点C落在AB上的点E处,求DB的长.
19. 如图,在 中, , , ,将 沿AD折叠,使点C落在AB上的点E处,求DB的长.
四、综合题
-
20. 在中, , 点E在边上,连结 , 将沿翻折使得点D落在边上得 , 连结 .
 (1)、如图1, , , 求的度数.(2)、如图2,若 , , 求的度数.21. 在直角坐标系中,的顶点坐标分别是 , , .
(1)、如图1, , , 求的度数.(2)、如图2,若 , , 求的度数.21. 在直角坐标系中,的顶点坐标分别是 , , . (1)、作关于轴对称的 , 并写出顶点 , , 的坐标;(2)、若以B,C,D为顶点的三角形与全等,请直接写出所有符合条件的点D的坐标.(点D与点A不重合.)22. 如图,在中, , 点为边上异于 , 的一个动点,作点关于的对称点 , 连结 , , 交直线于点.
(1)、作关于轴对称的 , 并写出顶点 , , 的坐标;(2)、若以B,C,D为顶点的三角形与全等,请直接写出所有符合条件的点D的坐标.(点D与点A不重合.)22. 如图,在中, , 点为边上异于 , 的一个动点,作点关于的对称点 , 连结 , , 交直线于点. (1)、若 , , 是边上的高线.
(1)、若 , , 是边上的高线.①求线段的长;
②当时,求线段的长;
(2)、在的情况下,当是等腰三角形时,直接写出的度数.23. 如图,在边长为的正方形中,过中点E作正 , 过点F的直线分别交边、于点G、H、已知点M、N分别是线段、的动点,且是等边三角形.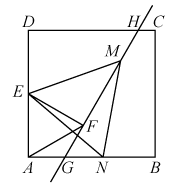 (1)、判断与的位置关系,并说明理由.(2)、当点N在线段上时
(1)、判断与的位置关系,并说明理由.(2)、当点N在线段上时①求证:
②试判断的结果是否变化?若变化,请说明理由;若不变,请求出这个值.
(3)、设 , 点A关于的对称点为 , 若点落在的内部,请直接写出的范围.