（苏科版）2023-2024学年八年级上学期微专题提分精炼——三角形全等的判定

试卷更新日期：2023-06-29 类型：复习试卷

进入出卷网下载

一、选择题

1. 下面各图中所给数据的三角形，则甲、乙、丙三个三角形和左侧 $△ A B C$ 全等的是（）

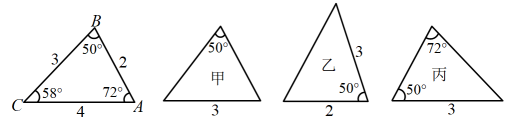A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙

查看试题解析
2. 如图，在 $△ A B C$ 中， $B D$ 平分 $∠ A B C$ 交AC于点D，且 $B D ⊥ A C$ ， F在BC上，E为AF的中点，连接DE，若 $B F = D E$ ， $A C = 2 \sqrt{3} D E$ ， $B D = 6$ ，则AB的长为（）

A、 $3 \sqrt{6}$ B、 $4 \sqrt{3}$ C、 $\sqrt{42}$ D、9

查看试题解析
3. 如图，有一块三角形的玻璃，不小心掉在地上打成三块，现要到玻璃店重新划一块与原来形状、大小一样的玻璃，只需带到玻璃店（）

A、① B、② C、③ D、①、②、③其中任一块

查看试题解析
4. 如图，在 $△ A B C$ 中， $A B = B C = A C$ ， $A E = C D$ ， $A D$ 与 $B E$ 相交于点 $P$ ， $B Q ⊥ A D$ 于 $Q$ .则下列数量关系正确的为（）

A、 $B P^{2} = 2 P Q^{2}$ B、 $3 B P^{2} = 4 B Q^{2}$ C、 $4 B P^{2} = 3 P Q^{2}$ D、 $2 B Q^{2} = 3 P Q^{2}$

查看试题解析
5. 如图，在△ABC中，AB＝AC，AD平分∠BAC，DE⊥AB于E点，DF⊥AC于点F，则下列四个结论：①AD上任意一点到AB，AC两边的距离相等； ②AD⊥BC且BD＝CD；③∠BDE＝∠CDF；④AE＝AF.其中正确的有（）

A、②③ B、①③ C、①②④ D、①②③④

查看试题解析
6. 如图是用尺规作 $∠ A O B$ 的平分线 $O C$ 的示意图，那么这样作图的依据是（）

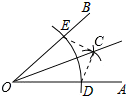A、SSS B、SAS C、ASA D、AAS

查看试题解析
7. 如图，边长为a的等边△ABC中，BF是AC上中线且BF＝b，点D在BF上，连接AD，在AD的右侧作等边△ADE，连接EF，则△AEF周长的最小值是（）

A、 $\frac{1}{2} a + \frac{2}{3} b$ B、 $\frac{1}{2} a + b$ C、a+ $\frac{1}{2}$ b D、 $\frac{3}{2}$ a

查看试题解析
8. 如图，在长方形纸片ABCD中，AB＝8cm，AD＝6cm.把长方形纸片沿直线AC折叠，点B落在点E处，AE交DC于点F，则AF的长为（）

A、 $\frac{25}{4}$ cm B、 $\frac{15}{2}$ cm C、7cm D、 $\frac{13}{2}$ cm

查看试题解析
9. 如图，正方形 $A B C D$ 的边长为 $10$ ， $A G = C H = 8$ ， $B G = D H = 6$ ，连结 $G H$ ，则线段 $G H$ 的长为（）

A、 $\frac{5 \sqrt{3}}{8}$ B、 $2 \sqrt{2}$ C、 $\frac{14}{5}$ D、 $10 - 5 \sqrt{2}$

查看试题解析
10. 如图，已知 $△ A B C$ ，小慧同学利用尺规作出 $△ A_{1} B_{1} C_{1}$ 与 $△ A B C$ 全等，根据作图痕迹请判断小慧同学的全等判定依据（）

A、SSS B、SAS C、AAS D、ASA

查看试题解析

二、填空题

11. 等腰 $△ A B C$ 中， $A B = A C$ ，顶角A为 $40 °$ ，平面内有一点P，满足 $A P = B C$ 且 $B P = B A$ ，则 $∠ P B C$ 的度数为 $°$ ．

查看试题解析
12. 如图，等腰 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ C A B$ ， $E D ⊥ A B$ 于 $E$ ，若 $A B = 6$ ，则 $△ B E D$ 的周长是．

查看试题解析
13. 如图，直线 $y = k x + 2$ 与x轴，y轴分别交于A，C两点，点B与点A关于y轴对称，连接 $B C$ ， $B C = 2 \sqrt{5}$ ，点M，N分别是线段 $A B ， A C$ 上的动点（M不与A，B重合），且满足 $∠ C M N = ∠ C B A$ .当 $△ C M N$ 为等腰三角形时，M的坐标为.

查看试题解析
14. 如图，在Rt△ABC中，AC＝4，AB＝5，∠C＝90°，BD平分∠ABC交AC于点D，则BD的长是.

查看试题解析
15. 如图，已知反比例函数经过 $A ， B$ 两点，A点坐标 $(1 ， 2)$ ， B点的横坐标为－2，将线段 $A B$ 绕点B顺时针旋转90°得到线段 $B C$ ，则C点坐标为.

查看试题解析

三、解答题

16. 已知：如图，点 $A ， D ， B ， E$ 在同一条直线上， $A C = E F ， A D = B E ， B C = D F$ .求证： $∠ E D F = ∠ A B C$ .

查看试题解析
17. 已知：如图，点B，F，C，E在一条直线上， $∠ B = ∠ E F D$ ， $∠ A C B = ∠ D E F$ ，且 $B F = E C$ .求证： $△ A B C ≌ △ D F E$ .

查看试题解析
18. 如图，已知在△ABC和△DBE中，AB＝DB，∠1＝∠2，∠A＝∠D．求证：BC＝BE．

查看试题解析
19. 如图，在 $△ A B C$ 中， $A D$ 平分 $∠ B A C$ ， $A D$ 也是 $B C$ 边上的中线.
求证： $A B = A C$ .

查看试题解析

四、综合题

20. 如图，在平行四边形ABCD中，点E、F为对角线BD的三等分点，连结AE，CF，AF，CE．

(1)、求证：四边形AECF为平行四边形；

(2)、若四边形AECF为菱形，且AE＝BE，求 $∠$ BAD的度数．

查看试题解析
21. 如图， $△ A B C$ 是等边三角形，D、E分别是边 $A B$ 、 $A C$ 上的点，且 $B D = A E$ ，且 $C D$ 、 $B E$ 交于点G，且 $D F ⊥ B E$ ，垂足为F．

(1)、求证： $∠ A C D = ∠ C B E$ ；

(2)、若 $F G = 1$ ，求DG的长度．

查看试题解析
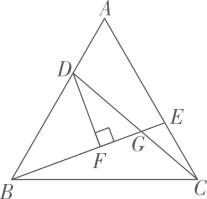22. 如图，点A在直线l上，在直线l右侧做等腰三角形 $A B C$ ， $A B = A C$ ， $∠ B A C = α$ ，点D与点B关于直线l轴对称，连接 $C D$ 交直线l于点E，连接 $B E$ .

(1)、求证： $∠ A D C = ∠ A C D$ ；

(2)、求证： $∠ B E C = α$ ；

(3)、当 $α = 90 °$ 时，求证： $E D^{2} + C E^{2} = 2 A B^{2}$ .

查看试题解析
23. 某校一数学兴趣小组在一次合作探究活动中，将两块大小不同的等腰直角三角形 $A B C$ 和等腰直角三角形 $C D E$ ，按如图1的方式摆放， $∠ A C B = ∠ E C D = 90 °$ ．该数学兴趣小组进行如下探究，请你帮忙解答：

(1)、【初步探究】如图1，试探究 $E D$ 与 $A B$ 的位置关系，并说明理由；

(2)、【深入探究】如图2，当 $B$ 、 $D$ 、 $E$ 三点共线时，请探究此位置时线段 $A E$ 、 $B E$ 、 $C E$ 之间的数量关系，并说明理由；

(3)、【拓展延伸】如图3，当 $B$ 、 $D$ 、 $E$ 三点不共线时，连接 $A E$ ，延长 $B D$ 交 $A E$ 于点 $F$ ，连接 $C F$ ，请猜想此位置时线段 $A F$ 、 $B F$ 、 $C F$ 之间的数量关系：．

查看试题解析