(苏科版)2023-2024学年八年级上学期微专题提分精炼——三角形全等及其性质
试卷更新日期:2023-06-29 类型:复习试卷
一、选择题
-
1. 如图, , 若 , 则的度数为( )
 A、20° B、25° C、30° D、50°2. 如图,在中, , , 分别是边 , 上的点, , CD与BE交于点F,则图中全等三角形的对数为( )
A、20° B、25° C、30° D、50°2. 如图,在中, , , 分别是边 , 上的点, , CD与BE交于点F,则图中全等三角形的对数为( ) A、2 B、3 C、4 D、53. 如图,点A,E,C在同一直线上, , , , 则BC的长为( )
A、2 B、3 C、4 D、53. 如图,点A,E,C在同一直线上, , , , 则BC的长为( ) A、3 B、5 C、8 D、114. 图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
A、3 B、5 C、8 D、114. 图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( ) A、51 B、49 C、76 D、无法确定5. 如图,△ABC≌△DEF,若∠A=100°,∠F=47°,则∠E的度数为( )
A、51 B、49 C、76 D、无法确定5. 如图,△ABC≌△DEF,若∠A=100°,∠F=47°,则∠E的度数为( )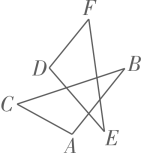 A、100° B、53° C、47° D、33°6. 如图, , , 记 , , 当时,α与β之间的数量关系为( )
A、100° B、53° C、47° D、33°6. 如图, , , 记 , , 当时,α与β之间的数量关系为( ) A、 B、 C、 D、7. 如图,△ABC中,D点在AB上,E点在BC上,DE为AB的中垂线.若∠B=∠C,且∠EAC>90°,则根据图中标示的角,下列结论正确的是( )
A、 B、 C、 D、7. 如图,△ABC中,D点在AB上,E点在BC上,DE为AB的中垂线.若∠B=∠C,且∠EAC>90°,则根据图中标示的角,下列结论正确的是( ) A、∠1=∠2,∠1<∠3 B、∠1=∠2,∠1>∠3 C、∠l≠∠2,∠1<∠3 D、∠1≠∠2,∠1>∠38. 如图的两个三角形是全等三角形,其中角和边的大小如图所示,那么∠1的度数是( )
A、∠1=∠2,∠1<∠3 B、∠1=∠2,∠1>∠3 C、∠l≠∠2,∠1<∠3 D、∠1≠∠2,∠1>∠38. 如图的两个三角形是全等三角形,其中角和边的大小如图所示,那么∠1的度数是( ) A、 B、 C、 D、9. 如图, , 过点作 , 垂足为 , 若 , 则的度数为( )
A、 B、 C、 D、9. 如图, , 过点作 , 垂足为 , 若 , 则的度数为( )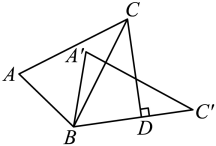 A、 B、 C、 D、10. 如图, , 于 , 于E,与交于点 . 有下列结论:
A、 B、 C、 D、10. 如图, , 于 , 于E,与交于点 . 有下列结论:①;②;③点在的平分线上;④点在的中垂线上.以上结论正确的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 如图,若 , 且 , , 则°.
 12. 如图,在平面直角坐标系中,点 , 的坐标分别是 , , , 若点在轴的正半轴上,则位于第四象限的点的坐标是 .
12. 如图,在平面直角坐标系中,点 , 的坐标分别是 , , , 若点在轴的正半轴上,则位于第四象限的点的坐标是 . 13. 三个全等三角形摆成如图所示的形式,则的度数为.
13. 三个全等三角形摆成如图所示的形式,则的度数为. 14. 如图, , 若 , 则的度数为 .
14. 如图, , 若 , 则的度数为 .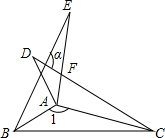 15. 如图,若 , , , , 则的周长为 .
15. 如图,若 , , , , 则的周长为 .
三、解答题
-
16. 如图,已知 , 点D在上,与交于点P.若 , , 求的度数.
 17. 如图,点D在上,点E在上, , 求证: .
17. 如图,点D在上,点E在上, , 求证: . 18. 如图,四个三角形纸片Rt△ABC,Rt△AB1C1 , Rt△AB2C2 , Rt△AB3C3完全重合,并按图示位置摆放.已知BC= , AB=1,求四边形CC1C2C3的面积.
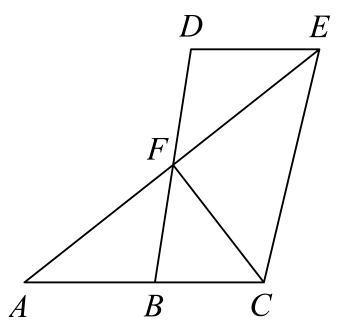
18. 如图,四个三角形纸片Rt△ABC,Rt△AB1C1 , Rt△AB2C2 , Rt△AB3C3完全重合,并按图示位置摆放.已知BC= , AB=1,求四边形CC1C2C3的面积. 19. 如图,已知点B、F、C、E在同一直线上,AB∥DE,AB=DE,BF=CE.求证:AC∥DF.
19. 如图,已知点B、F、C、E在同一直线上,AB∥DE,AB=DE,BF=CE.求证:AC∥DF.
四、综合题
-
20. 如图,已知 , 点为上一点,、分别平分、 , 交的延长线于点 .
 (1)、求证是等腰三角形;(2)、探索、、之间的等量关系,并说明理由.21. 问题1:如图①,在四边形ABCD中, , P是BC上一点, , .易得.(不需证明)
(1)、求证是等腰三角形;(2)、探索、、之间的等量关系,并说明理由.21. 问题1:如图①,在四边形ABCD中, , P是BC上一点, , .易得.(不需证明)问题2:如图②,在四边形ABCD中, , P是BC上一点, , .
 (1)、求证:;(2)、若 , 求与的面积和.
(1)、求证:;(2)、若 , 求与的面积和.

