(苏科版)2023-2024学年八年级上学期微专题提分精炼——全等图形
试卷更新日期:2023-06-29 类型:复习试卷
一、选择题
-
1. 下列四个图形中,属于全等图形的是( )
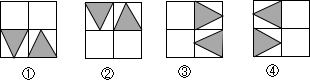 A、①和② B、②和③ C、①和③ D、③和④2. 关于全等图形的描述,下列说法正确的是( )A、形状相同的图形 B、面积相等的图形 C、能够完全重合的图形 D、周长相等的图形3. 观察下列图案,其中与如图全等的是( )
A、①和② B、②和③ C、①和③ D、③和④2. 关于全等图形的描述,下列说法正确的是( )A、形状相同的图形 B、面积相等的图形 C、能够完全重合的图形 D、周长相等的图形3. 观察下列图案,其中与如图全等的是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 下列四组图形中,是全等形的一组是( )A、
4. 下列四组图形中,是全等形的一组是( )A、 B、
B、 C、
C、 D、
D、 5. 下列说法错误的是( )A、如果两个图形全等,那么它们的形状和大小一定相同; B、图形全等,只与形状,大小有关,而与它们的位置无关; C、全等图形的面积相等,面积相等的两个图形是全等图形; D、全等三角形的对应边相等,对应角相等.6. 有下列说法,其中正确的有 ( )
5. 下列说法错误的是( )A、如果两个图形全等,那么它们的形状和大小一定相同; B、图形全等,只与形状,大小有关,而与它们的位置无关; C、全等图形的面积相等,面积相等的两个图形是全等图形; D、全等三角形的对应边相等,对应角相等.6. 有下列说法,其中正确的有 ( )①只有两个三角形才能完全重合;②如果两个图形全等,那么它们的形状和大小一定相同;③两个正方形一定是全等图形;④面积相等的两个图形一定是全等图形.
A、1个 B、2个 C、3个 D、4个7. 下列图形中被虚线分成的两部分不是全等图形的是( )A、 B、
B、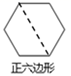 C、
C、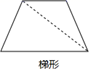 D、
D、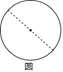 8. 如图,某人不小心将一块正五边形玻璃打碎成四块,若想到玻璃店配一块与原来一样大小的五边形玻璃,那么最省事的方法应该带玻璃碎片( )
8. 如图,某人不小心将一块正五边形玻璃打碎成四块,若想到玻璃店配一块与原来一样大小的五边形玻璃,那么最省事的方法应该带玻璃碎片( ) A、① B、①② C、①③ D、①③④9. 下列说法:①全等的两个图形一定成轴对称;②成轴对称的两个图形一定全等③轴对称图形的对称点一定在对称轴的两侧;④若点A、B关于直线MN对称,则直线MN垂直平分线段AB.正确的有( )A、1个 B、2个 C、3个 D、4个10. 如图是由四个全等的直角三角形与一个小正方形拼成的大正方形.若小正方形边长为 ,大正方形边长为 ,则一个直角三角形的面积等于( )
A、① B、①② C、①③ D、①③④9. 下列说法:①全等的两个图形一定成轴对称;②成轴对称的两个图形一定全等③轴对称图形的对称点一定在对称轴的两侧;④若点A、B关于直线MN对称,则直线MN垂直平分线段AB.正确的有( )A、1个 B、2个 C、3个 D、4个10. 如图是由四个全等的直角三角形与一个小正方形拼成的大正方形.若小正方形边长为 ,大正方形边长为 ,则一个直角三角形的面积等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形.画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画出个.
 12. 如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2=.
12. 如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2=.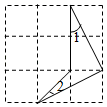 13. 如图,△ABC 中,点 A(0,1),点 C(4,3),如果要使△ABD 与△ABC 全等,那么符合条件的点 D 的坐标为.
13. 如图,△ABC 中,点 A(0,1),点 C(4,3),如果要使△ABD 与△ABC 全等,那么符合条件的点 D 的坐标为.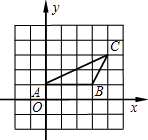 14. 规定:四条边对应相等,四个角对应相等的两个四边形全等.某学习小组在研究后发现判定两个四边形全等需要五组对应条件,于是把五组条件进行分类研究,并且针对二条边和三个角对应相等类型进行研究提出以下几种可能:
14. 规定:四条边对应相等,四个角对应相等的两个四边形全等.某学习小组在研究后发现判定两个四边形全等需要五组对应条件,于是把五组条件进行分类研究,并且针对二条边和三个角对应相等类型进行研究提出以下几种可能: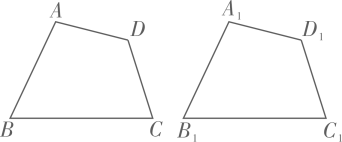
①AB=A1B1 , AD=A1D1 , ∠A=∠A1 , ∠B=∠B1 , ∠C=∠C1;
②AB=A1B1 , AD=A1D1 , ∠A=∠A1 , ∠B=∠B1 , ∠D=∠D1;
③AB=A1B1 , AD=A1D1 , ∠B=∠B1 , ∠C=∠C1 , ∠D=∠D1;
④AB=A1B1 , CD=C1D1 , ∠A=∠A1 , ∠B=∠B1 , ∠C=∠C1 .
其中能判定四边形ABCD和四边形A1B1C1D1全等的有个.
15.如图,在△ABC和△BAD中,BC=AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是 (只填一个).

三、解答题
-
16. 如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D。
 17. 图中所示的是两个全等的五边形,∠β=115°,d=5,指出它们的对应顶点•对应边与对应角,并说出图中标的a,b,c,e,α各字母所表示的值.
17. 图中所示的是两个全等的五边形,∠β=115°,d=5,指出它们的对应顶点•对应边与对应角,并说出图中标的a,b,c,e,α各字母所表示的值.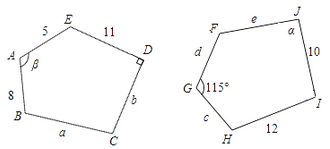 18.
18.如图所示是一个4×4的正方形,求∠1+∠2+∠3+…+∠16的度数.
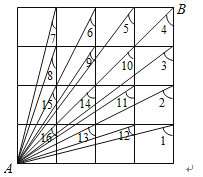 19.
19.图中所示的是两个全等的五边形,∠β=115°,d=5,指出它们的对应顶点•对应边与对应角,并说出图中标的a,b,c,e,α各字母所表示的值.
 20. 根据全等图形的定义,我们把能够完全重合(即四个内角、四条边分别对应相等)的四边形叫做全等四边形.请借助三角形全等的知识,解决有关四边形全等的问题.如图,已知,四边形 ABCD 和四边形 A'B'C'D'中,AB = A'B',BC = B'C',∠B = ∠B',∠C = ∠C',现在只需补充一个条件,就可得四边形 ABCD ≌四边形 A'B'C'D'. 下列四个条件:① ∠A = ∠A' ;② ∠D = ∠D' ;③ AD = A'D';④ CD = C'D'.
20. 根据全等图形的定义,我们把能够完全重合(即四个内角、四条边分别对应相等)的四边形叫做全等四边形.请借助三角形全等的知识,解决有关四边形全等的问题.如图,已知,四边形 ABCD 和四边形 A'B'C'D'中,AB = A'B',BC = B'C',∠B = ∠B',∠C = ∠C',现在只需补充一个条件,就可得四边形 ABCD ≌四边形 A'B'C'D'. 下列四个条件:① ∠A = ∠A' ;② ∠D = ∠D' ;③ AD = A'D';④ CD = C'D'. (1)、其中,符合要求的条件是.(直接写出编号)(2)、选择(1)中的一个条件,证明四边形 ABCD ≌四边形 A'B'C'D' .
(1)、其中,符合要求的条件是.(直接写出编号)(2)、选择(1)中的一个条件,证明四边形 ABCD ≌四边形 A'B'C'D' .