湖北省襄阳市老河口市2022-2023学年八年级下学期数学6月月考试卷

试卷更新日期：2023-06-29 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10个小题，每小题3分，共30分）

1. 下列线段不能构成直角三角形的是（）

A、9，12，15 B、7，24，25 C、 $\sqrt{3}$ ， 2， $\sqrt{5}$ D、9，40，41

查看试题解析
2. 下列计算正确的是（　　）

A、 $\sqrt{20} = 2 \sqrt{10}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{12} \div 2 = 2 \sqrt{3}$

查看试题解析
3. 点A( $\sqrt{2}$ ， m)，B( $\frac{3}{2}$ ， n)都在一次函数y＝2x＋1的图象上，则m与n的大小关系是（）

A、m＞n B、m＝n C、m＜n D、无法确定

查看试题解析
4. 为考察种植的杂交水稻苗的长势，从稻田中随机抽取9株水稻苗，测得苗高(单位：cm)分别是：22，23，24，23，24，25，26，23，25，则这组数据的众数和中位数分别是（）

A、24cm，25cm B、23cm，23cm C、23cm，24cm D、24cm，24cm

查看试题解析
5. 如图，在Rt△ABC中，∠ACB＝90°，AD为中线，点E为AD的中点，点F为BE的中点．若AC＝8，BC＝12，则DF的长为（）

A、2 B、2.5 C、3 D、4

查看试题解析
6. 甲、乙两人从相距3600m的A，B两地相向而行，他们离B地的路程s(m)与从出发到相遇的运动时间t(单位：min)之间的函数关系如图．甲骑车、乙步行，甲的速度是乙的3倍，相遇后，乙坐甲的车原路返回．若甲骑车的速度一直不变，则乙返回所用时间是（）

A、5min B、15min C、20min D、30min

查看试题解析
7. 某市移动通信公司推出两种上网的收费方式，其月费用 $y$ (单位：元)关于月上网时间 $x$ (单位： $h)$ 的函数解析式分别为： $y_{1} = {\begin{array}{l} a (0 \leq a \leq 50) \\ 3 x - 100 (x > 50) \end{array} ， y_{2} = {\begin{array}{l} b (0 \leq x \leq 25) \\ 3 x - 45 (x > 25) \end{array}$ ， a，b为常数，这两种收费方式的函数图象如图所示，当两种收费方式的月费用相同时，月上网时间是（）.

A、 $\frac{130}{3} h$ B、 $\frac{75}{3} h$ C、 $25 h$ D、 $\frac{95}{3} h$

查看试题解析
8. 如图，四边形OABC是边长为 $\sqrt{2}$ 的正方形，OC与x轴正半轴的夹角为15°，点B在直线y＝ax－2上，则a的值为（）

A、2 B、 $\frac{1}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{2}{3}$

查看试题解析
9. 如图，小明(视为小黑点)站在一个高为10m的高台A上，利用旗杆OM顶部的绳索划过90°到达与高台A水平距离为17m，高为3m的矮台B，则小明在荡绳索的过程中离地面的最低点的高度MN是（）

A、2m B、2.2m C、2.5m D、2.7m

查看试题解析
10. 如图，四边形ABCD中，AD⊥CD于点D，BC＝2，AD＝8，CD＝6，点E是AB的中点，连接DE，则DE的最大值是（）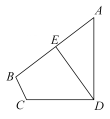

A、6 B、7 C、8 D、9

查看试题解析

二、填空题（本大题共8小题，每小题3分，共24分）

11. 函数 $y = \frac{\sqrt{x} - 2}{x - 3}$ 中自变量x的取值范围是.

查看试题解析
12. 若一次函数y＝kx＋b的图象如图所示，则关于x的方程kx＋b＝3的解为．

查看试题解析
13. 甲、乙两个篮球队队员身高的平均数都为2.07米，方差分别是s甲2，s乙2，且s甲2>s乙2，则队员身高比较整齐的球队是.

查看试题解析
14. 将直线y＝2x－1沿y轴平移3个单位长度，则平移后的直线与y轴的交点的坐标为．

查看试题解析
15. 如图，在正方形ABCD中，G是对角线BD上的点，GE⊥CD，GF⊥BC，E，F分别为垂足，连接EF．设M，N分别是AB，BG的中点，EF＝5，则MN的长为．

查看试题解析
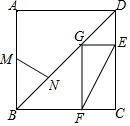16. 如图①，点P从△ABC的顶点B出发，沿B→C→A匀速运动到点A，图②是点P运动时，线段BP的长度y随时间x变化的关系图象，其中M为曲线部分的最低点，则△ABC的面积是．

查看试题解析
17. 如图， ▱ ABCD的顶点C在等边△BEF的边BF上，点E在AB的延长线上，G为DE的中点，连接CG.若AD＝3，AB＝CF＝2，则CG的长为．

查看试题解析
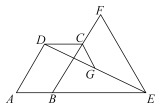18. 如图，在矩形ABCD中，AB＝4，AD＝2，E为AB的中点，F为EC上的一动点，P为DF的中点，连接PB，则PB的最小值是．

查看试题解析

三、填空题（本大题共8个空，每空3分，共24分）

19. 计算：

(1)、 $(\sqrt{6} - 2 \sqrt{5}) \times \sqrt{3} - 6 \sqrt{\frac{1}{2}}$ ；

(2)、 $\sqrt{27} \times \sqrt{\frac{1}{3}} - (\sqrt{5} + \sqrt{3}) (\sqrt{5} - \sqrt{3})$

查看试题解析
20. 如图，在Rt△ABC中，∠ABC＝90°.

(1)、求作点D，使四边形ABCD是矩形；(要求：尺规作图，不写作法，保留作图痕迹)

(2)、在⑴的条件下，连接BD，若AB＝3，BC＝1，求BD的长．

查看试题解析
21. 某校260名学生参加植树活动，要求每人植4～7棵，结束后随机抽查了若干名学生每人的植树量，并分为四种类型：A：4棵；B：5棵；C：6棵；D：7棵，将各类的人数绘制成如图所示的两幅不完整的统计图，请根据图中信息解决下列问题：

(1)、在这次调查中D类型有多少名学生？

(2)、写出被调查的学生每人植树量的众数和中位数；

(3)、求被调查的学生每人植树量的平均数，并估计这260名学生共植树多少棵．

查看试题解析
22. 如图，一次函数y＝kx＋b的图象经过点A(－2，6)，且与x轴相交于点B，与正比例函数y＝3x的图象相交于点C，点C的横坐标为1.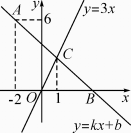

(1)、求k，b的值；

(2)、若点D在y轴负半轴上，且满足S△COD＝ $\frac{1}{3}$ S△BOC，求点D的坐标．

查看试题解析
23. 如图，ABCD的对角线AC，BD交于点O，过点O的直线交BC于点E，交AD于点F.

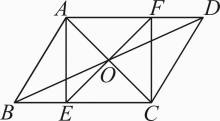(1)、判断四边形AECF的形状，并说明理由；

(2)、当OE与AC有何关系时，四边形AECF为正方形？请说明理由．

查看试题解析
24. 某水果店以每千克9元的价格购进苹果若干千克，销售了部分苹果后，余下的苹果每千克降价4元销售，全部售完．销售金额y(元)与销售量x(千克)之间的关系如图所示，请根据图象提供的信息完成下列问题：

(1)、降价前苹果的销售单价是元/千克；

(2)、求降价后销售金额y(元)与销售量x(千克)之间的函数解析式，并写出自变量的取值范围；

(3)、为了抗震救灾，该水果店决定所卖出的苹果每千克捐出m元，若要保证利润率不低于40%，则m的最大值是多少？

查看试题解析
25. 在平面直角坐标系中，O是坐标原点，直线y＝kx＋15(k≠0)经过点C(3，6)，与x轴交于点A，与y轴交于点B.线段CD平行于x轴，交直线y＝ $\frac{3}{4}$ x于点D，连接OC，AD.

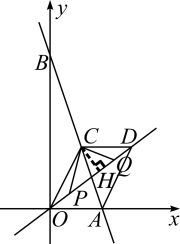(1)、填空：k＝，点A的坐标是；

(2)、求证：四边形OADC是平行四边形；

(3)、动点P从点O出发，沿对角线OD以每秒1个单位长度的速度向点D运动，直到点D为止；动点Q同时从点D出发，沿对角线DO以每秒1个单位长度的速度向点O运动，直到点O为止．连接CP、CQ，设两个点的运动时间均为ts.
①当t＝1时，求△CPQ的面积；
②连接AP，AQ，当点P，Q运动至四边形CPAQ为矩形时，请直接写出此时t的值．

查看试题解析