湖北省荆州市2023年中考数学试卷
试卷更新日期:2023-06-29 类型:中考真卷
一、选择题(本大题共有10个小题,每小题只有唯一正确答案,每小题3分,共30分)
-
1. 在实数-1, , , 3.14中,无理数是( )A、-1 B、 C、 D、3.142. 下列各式运算正确的是( )A、 B、 C、 D、3. 观察如图所示的几何体,下列关于其三视图的说法正确的是( )
 A、主视图既是中心对称图形,又是轴对称图形 B、左视图既是中心对称图形,又是轴对称图形 C、俯视图既是中心对称图形,又是轴对称图形 D、主视图、左视图、俯视图都是中心对称图形4. 已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系().下列反映电流I与电阻R之间函数关系的图象大致是( )A、
A、主视图既是中心对称图形,又是轴对称图形 B、左视图既是中心对称图形,又是轴对称图形 C、俯视图既是中心对称图形,又是轴对称图形 D、主视图、左视图、俯视图都是中心对称图形4. 已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系().下列反映电流I与电阻R之间函数关系的图象大致是( )A、 B、
B、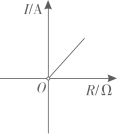 C、
C、 D、
D、 5. 已知 , 则与最接近的整数为( )A、2 B、3 C、4 D、56. 为评估一种水稻的种植效果,选了10块地作试验田.这10块地的亩产量(单位:kg)分别为x1 , x2 , …,x10 , 下面给出的统计量中可以用来评估这种水稻亩产量稳定程度的是( )A、这组数据的平均数 B、这组数据的方差 C、这组数据的众数 D、这组数据的中位数7. 如图所示的“箭头”图形中,AB∥CD, , 则图中∠G的度数是( )
5. 已知 , 则与最接近的整数为( )A、2 B、3 C、4 D、56. 为评估一种水稻的种植效果,选了10块地作试验田.这10块地的亩产量(单位:kg)分别为x1 , x2 , …,x10 , 下面给出的统计量中可以用来评估这种水稻亩产量稳定程度的是( )A、这组数据的平均数 B、这组数据的方差 C、这组数据的众数 D、这组数据的中位数7. 如图所示的“箭头”图形中,AB∥CD, , 则图中∠G的度数是( ) A、 B、 C、 D、8. 我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还余4.5尺;将绳子对折再量木条,木条余1尺,问木条长多少尺?若设木条长x尺,绳子长y尺,则可列方程组为( )A、 B、 C、 D、9. 如图,直线分别与x轴,y轴交于点A,B,将△OAB绕着点A顺时针旋转得到△CAD,则点B的对应点D的坐标是( )
A、 B、 C、 D、8. 我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还余4.5尺;将绳子对折再量木条,木条余1尺,问木条长多少尺?若设木条长x尺,绳子长y尺,则可列方程组为( )A、 B、 C、 D、9. 如图,直线分别与x轴,y轴交于点A,B,将△OAB绕着点A顺时针旋转得到△CAD,则点B的对应点D的坐标是( ) A、(2,5) B、(3,5) C、(5,2) D、( , 2)10. 如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,B为上一点,OB⊥AC于D. 若AC=m,BD=150m,则的长为( )
A、(2,5) B、(3,5) C、(5,2) D、( , 2)10. 如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,B为上一点,OB⊥AC于D. 若AC=m,BD=150m,则的长为( ) A、m B、m C、m D、m
A、m B、m C、m D、m二、填空题(本大题共6个小题,每小题3分,共18分)
-
11. 若 , 则= .12. 如图,CD为Rt△ABC斜边AB上的中线,E为AC的中点.若 , , 则DE= .
 13. 某校为了解学生对A,B,C,D四类运动的参与情况,随机调查了本校80名学生,让他们从中选择参与最多的一类,得到对应的人数分别是30,20,18,12.若该校有800名学生,则估计有人参与A类运动最多.14. 如图,∠AOB=60o , 点C在OB上,OC= , P为∠AOB内一点.根据图中尺规作图痕迹推断,点P到OA的距离为 .
13. 某校为了解学生对A,B,C,D四类运动的参与情况,随机调查了本校80名学生,让他们从中选择参与最多的一类,得到对应的人数分别是30,20,18,12.若该校有800名学生,则估计有人参与A类运动最多.14. 如图,∠AOB=60o , 点C在OB上,OC= , P为∠AOB内一点.根据图中尺规作图痕迹推断,点P到OA的距离为 . 15. 如图,无人机在空中A处测得某校旗杆顶部B的仰角为30o , 底部C的俯角为60o , 无人机与旗杆的水平距离AD为6m,则该校的旗杆高约为m.( , 结果精确到0.1)
15. 如图,无人机在空中A处测得某校旗杆顶部B的仰角为30o , 底部C的俯角为60o , 无人机与旗杆的水平距离AD为6m,则该校的旗杆高约为m.( , 结果精确到0.1)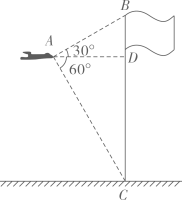 16. 如图,点A(2,2)在双曲线上,将直线OA向上平移若干个单位长度交y轴于点B,交双曲线于点C. 若BC=2,则点C的坐标是 .
16. 如图,点A(2,2)在双曲线上,将直线OA向上平移若干个单位长度交y轴于点B,交双曲线于点C. 若BC=2,则点C的坐标是 .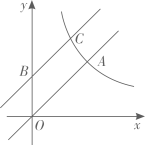
三、解答题(本大题共有8个小题,共72分)
-
17. 先化简,再求值:
, 其中
18. 已知关于的一元二次方程有两个不相等的实数根.(1)、求的取值范围;(2)、当时,用配方法解方程.19. 如图,BD是等边△ABC的中线,以D为圆心,DB的长为半径画弧,交BC的延长线于E,连接DE.求证:CD=CE. 20. 首届楚文化节在荆州举办前,主办方为使参与服务的志愿者队伍整齐,随机抽取了部分志愿者,对其身高进行调查,将身高(单位:cm)数据分A,B,C,D,E五组制成了如下的统计图表(不完整).
20. 首届楚文化节在荆州举办前,主办方为使参与服务的志愿者队伍整齐,随机抽取了部分志愿者,对其身高进行调查,将身高(单位:cm)数据分A,B,C,D,E五组制成了如下的统计图表(不完整).组别
身高分组
人数
A
155≤x<160
3
B
160≤x<165
2
C
165≤x<170
m
D
170≤x<175
5
E
175≤x<180
4

根据以上信息回答:
(1)、这次被调查身高的志愿者有人,表中的 , 扇形统计图中α的度数是;(2)、若E组的4人中,男女各有2人,以抽签方式从中随机抽取两人担任组长.请列表或画树状图,求刚好抽中两名女志愿者的概率.21. 如图,在菱形ABCD中,于H,以DH为直径的⊙O分别交AD,BD于点E,F,连接EF. (1)、求证:①CD是⊙O的切线;②△DEF∽△DBA;(2)、 若AB=5,DB=6 ,求 .22. 荆州古城旁“荆街”某商铺打算购进A,B两种文创饰品对游客销售.已知1400元采购A种的件数是630元采购B种件数的2倍,A种的进价比B种的进价每件多1元,两种饰品的售价均为每件15元;计划采购这两种饰品共600件,采购B种的件数不低于390件,不超过A种件数的4倍.(1)、求A,B饰品每件的进价分别为多少元?(2)、若采购这两种饰品只有一种情况可优惠,即一次性采购A种超过150件时,A种超过的部分按进价打6折.设购进A种饰品x件,①求x的取值范围;②设计能让这次采购的饰品获利最大的方案,并求出最大利润.23. 如图1,点P是线段AB上与点A,点B不重合的任意一点,在AB的同侧分别以A,P,B为顶点作 ∠1=∠2=∠3,其中∠1与∠3的一边分别是射线AB和射线BA,∠2的两边不在直线AB上,我们规定这三个角互为等联角,点P为等联点,线段AB为等联线.
(1)、求证:①CD是⊙O的切线;②△DEF∽△DBA;(2)、 若AB=5,DB=6 ,求 .22. 荆州古城旁“荆街”某商铺打算购进A,B两种文创饰品对游客销售.已知1400元采购A种的件数是630元采购B种件数的2倍,A种的进价比B种的进价每件多1元,两种饰品的售价均为每件15元;计划采购这两种饰品共600件,采购B种的件数不低于390件,不超过A种件数的4倍.(1)、求A,B饰品每件的进价分别为多少元?(2)、若采购这两种饰品只有一种情况可优惠,即一次性采购A种超过150件时,A种超过的部分按进价打6折.设购进A种饰品x件,①求x的取值范围;②设计能让这次采购的饰品获利最大的方案,并求出最大利润.23. 如图1,点P是线段AB上与点A,点B不重合的任意一点,在AB的同侧分别以A,P,B为顶点作 ∠1=∠2=∠3,其中∠1与∠3的一边分别是射线AB和射线BA,∠2的两边不在直线AB上,我们规定这三个角互为等联角,点P为等联点,线段AB为等联线.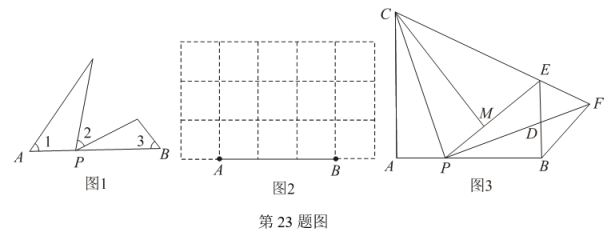 (1)、如图2,在5×3个方格的纸上,小正方形的顶点为格点、边长均为1,AB为端点在格点的已知线段.请用三种不同连接格点的方法,作出以线段AB为等联线、某格点P为等联点的等联角,并标出等联角,保留作图痕迹;(2)、如图3,在Rt△APC中,∠A=90°, , 延长AP至点B,使AB=AC,作∠A的等联角∠CPD和∠PBD.将△APC沿PC折叠,使点A落在点M处,得到△MPC,再延长PM交BD的延长线于E,连接CE并延长交PD的延长线于F,连接BF.
(1)、如图2,在5×3个方格的纸上,小正方形的顶点为格点、边长均为1,AB为端点在格点的已知线段.请用三种不同连接格点的方法,作出以线段AB为等联线、某格点P为等联点的等联角,并标出等联角,保留作图痕迹;(2)、如图3,在Rt△APC中,∠A=90°, , 延长AP至点B,使AB=AC,作∠A的等联角∠CPD和∠PBD.将△APC沿PC折叠,使点A落在点M处,得到△MPC,再延长PM交BD的延长线于E,连接CE并延长交PD的延长线于F,连接BF.①确定△PCF的形状,并说明理由;
②若AP:PB=1:2,BF=k,求等联线AB和线段PE的长(用含k的式子表示).
24. 已知:y关于x的函数 . (1)、若函数的图象与坐标轴有两个公共点,且 , 则a的值是;(2)、如图,若函数的图象为抛物线,与x轴有两个公共点A(-2,0),B(4,0),并与动直线l:交于点P,连接PA,PB,PC,BC,其中PA交y轴于点D,交BC于点E.设△PBE的面积为 , △CDE的面积为 .
(1)、若函数的图象与坐标轴有两个公共点,且 , 则a的值是;(2)、如图,若函数的图象为抛物线,与x轴有两个公共点A(-2,0),B(4,0),并与动直线l:交于点P,连接PA,PB,PC,BC,其中PA交y轴于点D,交BC于点E.设△PBE的面积为 , △CDE的面积为 .①当点P为抛物线顶点时,求△PBC的面积;
②探究直线l在运动过程中,-是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.