(北师大版)2023-2024学年七年级数学上册2.11 有理数的混合运算 同步测试
试卷更新日期:2023-06-28 类型:同步测试
一、选择题
-
1. 如图,各网格中四个数之间都有相同的规律,则第7个网格中右下角的数为( )
 A、62 B、79 C、88 D、982. 如果定义运算符号“”为 , 那么的值为( )A、12 B、11 C、10 D、93. 如图,文化广场上摆了一些桌子,若并排摆 25 张桌子,可同时容纳( )人
A、62 B、79 C、88 D、982. 如果定义运算符号“”为 , 那么的值为( )A、12 B、11 C、10 D、93. 如图,文化广场上摆了一些桌子,若并排摆 25 张桌子,可同时容纳( )人 A、106 B、98 C、100 D、1024. 正整数按如图所示的规律排列,则第9行、第列的数字是( )
A、106 B、98 C、100 D、1024. 正整数按如图所示的规律排列,则第9行、第列的数字是( ) A、 B、 C、 D、5. 下列四个式子中,计算结果最大的是( )A、-23+(-1)2 B、-23-(-1)2 C、-23×(-1)2 D、-23÷(-1)26. 如图1是一根起点为0且标有单位长度的射线,现有同学将它弯折成如图2,弯折后落在虚线上的点,从下往上第一个数是0,第二个数是12,第三个数是42,……,依此规律,落在虚线上的第五个点对应的数是( )
A、 B、 C、 D、5. 下列四个式子中,计算结果最大的是( )A、-23+(-1)2 B、-23-(-1)2 C、-23×(-1)2 D、-23÷(-1)26. 如图1是一根起点为0且标有单位长度的射线,现有同学将它弯折成如图2,弯折后落在虚线上的点,从下往上第一个数是0,第二个数是12,第三个数是42,……,依此规律,落在虚线上的第五个点对应的数是( )
 A、90 B、96 C、150 D、1567. 右图是“大润发”超市中“飘柔”洗发水的价格标签,一服务员不小心将墨水滴在标签上,使得原价看不清楚,该洗发水的原价为( )
A、90 B、96 C、150 D、1567. 右图是“大润发”超市中“飘柔”洗发水的价格标签,一服务员不小心将墨水滴在标签上,使得原价看不清楚,该洗发水的原价为( ) A、22元 B、23元 C、24元 D、26元8. 如果 互为相反数,互为倒数,m是最大的负整数,则的值是( )A、 B、 C、0 D、19. 按照如图所示的计算程序,若x=2,则输出的结果是( )
A、22元 B、23元 C、24元 D、26元8. 如果 互为相反数,互为倒数,m是最大的负整数,则的值是( )A、 B、 C、0 D、19. 按照如图所示的计算程序,若x=2,则输出的结果是( ) A、16 B、-16 C、26 D、-2610. 九宫格起源于中国古代的神秘图案河图和洛书.如图,将 , , , , , , , , 填入九宫格内,使每行、每列、每条对角线上三个数的和都相等,则的值为( )
A、16 B、-16 C、26 D、-2610. 九宫格起源于中国古代的神秘图案河图和洛书.如图,将 , , , , , , , , 填入九宫格内,使每行、每列、每条对角线上三个数的和都相等,则的值为( )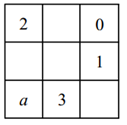 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 将相同的长方形卡片按如图方式摆放在一个直角上,每个长方形卡片长为2,宽为1,依此类推,摆放2023个时,实线部分长为.
 12. 已知整数a,b,c,且 , 满足 , 则的最小值为.13. 整数a、b、c满足1000|a|+10|b|+|c|=2023,其中|a|>1且abc>1,则a+b+c的最小值是 .14. 现定义一种新运算“*”,规定a*b=a2-b,如3*1=32-1=8,则(-2)*(-3)等于 .15. 某食品厂从生产的袋装食品中抽出样品10袋,检测每袋的质量是否符合标准,超过或不足的部分用正数或负数来表示,记录如下表:
12. 已知整数a,b,c,且 , 满足 , 则的最小值为.13. 整数a、b、c满足1000|a|+10|b|+|c|=2023,其中|a|>1且abc>1,则a+b+c的最小值是 .14. 现定义一种新运算“*”,规定a*b=a2-b,如3*1=32-1=8,则(-2)*(-3)等于 .15. 某食品厂从生产的袋装食品中抽出样品10袋,检测每袋的质量是否符合标准,超过或不足的部分用正数或负数来表示,记录如下表:与标准质量的差值/g
0
1
2
3
袋数
1
3
2
1
2
1
若每袋标准质量为 , 则抽样检测的总质量为 .
三、解答题
-
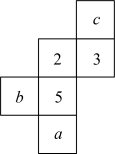
16. 数学老师规定了一种新运算:若 , 是有理数,则 , 请你计算:;.17. 如图所示的是一个正方体的展开图,将展开图折叠成正方体后相对的两个面的两个数互为相反数,求的值.
 18. 某种茶叶,若直接销售,每千克可获利润12元;若粗加工后销售,每千克可获利润50元;若精加工后销售,每千克可获利润75元.某茶叶加工厂现有这种茶叶140千克,该工厂的生产能力是:如果进行粗加工,每天可加工16千克;如果进行精加工,每天可加工6千克,但两种加工方式不能同时进行.受各种条件限制,工厂必须在15天内(含15天)将这批茶叶全部销售或加工完毕,为此该工厂营销科设计了三种方案:
18. 某种茶叶,若直接销售,每千克可获利润12元;若粗加工后销售,每千克可获利润50元;若精加工后销售,每千克可获利润75元.某茶叶加工厂现有这种茶叶140千克,该工厂的生产能力是:如果进行粗加工,每天可加工16千克;如果进行精加工,每天可加工6千克,但两种加工方式不能同时进行.受各种条件限制,工厂必须在15天内(含15天)将这批茶叶全部销售或加工完毕,为此该工厂营销科设计了三种方案:方案一:全部进行粗加工;
方案二:15天全部进行精加工,没有来得及进行精加工的利润;
方案三:将60千克进行精加工,其余的进行粗加工.
你认为选择哪种方案可获利润最多,为什么?最多可获利润多少元?
19. 有8筐白菜,以每筐25kg为准,超过的千克数记为正数,不足的千克数记为负数,称后的记录如下:1.5,-3,2,-0.5,1,-2.-2、-2.5。这8筐白菜一共多少千克?四、综合题
-
20. 某志愿者驾驶汽车在东西走向的道路上来回的运输防疫物资.若约定向东行驶记为正,已知某天他从道路上的A地出发到运输物资结束的行驶记录如下(单位:千米);(1)、运输物资结束时,汽车停在A地哪一边,距离A地多远?(2)、若汽车的耗油量为0.1升每千米,求这天汽车运输物资耗油多少升?21. 在实数范围内定义运算“※”: , 例如:.(1)、若 , , 计算的值.(2)、若 , 求x的值.(3)、若 , 求的值.22. 某治安巡警分队常常在一条东西走向的街道上巡逻一天 下午,该巡警分队驾驶电动小汽车从位于这条街道上的某岗亭出发巡逻,如果规定向东为正,向西为负,他们行驶里程(单位: km)如下:问:(1)、这辆小汽车完成巡逻后位于该岗亭的那一侧?距离岗亭有多少千米?(2)、已知这种电动小汽车平均每千米耗电度,则这天下午小汽车共耗电多少度?23. 某食品厂在产品中抽出袋样品,检查其质量是否达标,超过标准的部分用正数表示,不足的部分用负数表示:
与标准质量的差/克
0
1
袋数
1
4
3
4
3
2
3
(1)、这批样品的总质量比标准总质量多还是少?多或少几克?(2)、若每袋的标准质量为克,求这批样品平均每袋的质量是多少克?