（北师大版）2023-2024学年八年级数学上册2.7 二次根式同步测试

试卷更新日期：2023-06-28 类型：同步测试

进入出卷网下载

一、选择题

1. 下列式子中，属于最简二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{5}$ C、 $\sqrt{0.2}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
2. 下列运算结果正确的是（　　）

A、 $\sqrt{3} + \sqrt{7} = \sqrt{10}$ B、 $3 + \sqrt{7} = 3 \sqrt{7}$ C、 $\sqrt{3} \times \sqrt{7} = \sqrt{21}$ D、 $2 \sqrt{7} - 7 = \sqrt{7}$

查看试题解析
3. 要使得代数式 $\sqrt{x - 2}$ 有意义，则x的取值范围是（）

A、 $x > 2$ B、 $x \geq 2$ C、 $x < 2$ D、 $x \leq 2$

查看试题解析
4. 下列命题中，真命题的是（）
①若 $\sqrt{{(x - 2)}^{2}} = 2 - x$ ，则 $x < 2$ ②两直线平行，同旁内角相等③若一组数据 $2 ， 4 ， x ， - 1$ 极差为 7 ，则 $x$ 的值是 6 或 $- 3$ .④已知点 $P (m ， n)$ 在一次函数 $y = - 2 x + 3$ 的图象上，则 $2 m + n - 1 = 2$

A、①③ B、②④ C、①② D、③④

查看试题解析
5. 若 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x > 2$ B、 $x \geq 2$ C、 $x < 2$ D、 $x \neq 2$

查看试题解析
6. 若 $\sqrt{{(x - 3)}^{2}} = x - 3$ ，则 $x$ 的取值范围是（）

A、 $x > 3$ B、 $x ≥ 3$ C、 $x < 3$ D、 $x \leq 3$

查看试题解析
7. 函数 $y = \sqrt{x + 1} - {(x - 1)}^{0}$ 自变量 $x$ 的取值范围是（）

A、 $x \geq - 1$ B、 $x > - 1$ C、 $x > - 1$ 且 $x \neq 1$ D、 $x \geq - 1$ 且 $x \neq 1$

查看试题解析
8. 实数 $a ， b ， c$ 在数轴上的对应点如图所示，化简 $- a + | b - a | + \sqrt{c^{2}}$ 的结果是是（）

A、 $- b - c$ B、 $c - b$ C、 $2 - 2 b + 2 c$ D、 $2 + b + c$

查看试题解析
9. 要使二次根式 $\sqrt{x - 2}$ 有意义，x的值可以是（）

A、3 B、1 C、0 D、-1

查看试题解析
10. 实数 $a 、 b$ 在数轴上的位置如图所示，请化简： $\sqrt{a^{2}} - \sqrt{b^{2}}$ =（）

A、 $a - b$ B、 $- a + b$ C、 $- a - b$ D、 $a + b$

查看试题解析

二、填空题

11. 已知m为正整数，若 $\sqrt{189 m}$ 是整数，则根据 $\sqrt{189 m} = \sqrt{3 \times 3 \times 3 \times 7 m} = 3 \sqrt{3 \times 7 m}$ 可知m有最小值 $3 \times 7 = 21$ ．设n为正整数，若 $\sqrt{\frac{200}{n}}$ 是大于1的整数，则n的最小值为．

查看试题解析
12. 已知 $1 < x < 2$ ，则 $\sqrt{{(x - 2)}^{2}} + | x - 1 | =$ .

查看试题解析
13. 若a、b是等腰三角形 $A B C$ 的两条边，且 $\sqrt{a - 3} + | b - 6 | = 0$ ，则 $△ A B C$ 的周长为.

查看试题解析
14. 已知 $\sqrt{x - 3}$ 是二次根式，则x的取值范围是．

查看试题解析
15. 在进行二次根式化简时，我们可以将 $\frac{2}{\sqrt{3} + 1}$ 进一步化简，如：
$\frac{2}{\sqrt{3} + 1}$ = $\frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)}$ = $\frac{2 (\sqrt{3} - 1)}{(\sqrt{3})^{2} - 1^{2}}$ = $\sqrt{3} - 1$
则 $\frac{2}{1 + \sqrt{5}} + \frac{2}{\sqrt{5} + \sqrt{9}} + \frac{2}{\sqrt{9} + \sqrt{13}} + . . . + \frac{2}{\sqrt{4 n - 1} + \sqrt{4 n + 3}} =$ .

查看试题解析

三、解答题

16. 先化简： $\frac{a \sqrt{b} + b \sqrt{a}}{\sqrt{a} + \sqrt{b}} \cdot \sqrt{a b}$ ，再求当 $a = \frac{1}{\sqrt{2} + 1}$ ， $b = \frac{1}{\sqrt{2} - 1}$ 时的值．

查看试题解析
17. 实数a、b、c在数轴上的对应点位置如图所示，化简： $\sqrt{(- c)^{2}} + | a - b | + \sqrt[3]{(a + b)^{3}}$ -|b-c|

查看试题解析
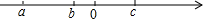18. 从理论上讲，人眼能看清楚无限远处的物体，但受光线等外在条件和人的眼球本身的健康程度等影响，实际上无法做到．天气晴朗时，一个人能看到大海的最远距离s可用经验公式 $s^{2} = 17 h$ 来估计，其中h是眼睛离海平面的高度（公式中s的单位是千米，h的单位是米）．某游客站在海边一处观景台上，眼睛距离海平面的高度约为34米，他能看到大海的最远距离约是多少千米？（结果保留整数， $\sqrt{2} \approx 1.4$ ）

查看试题解析
19. 在△ABC中，三边长分别为a，b，c，且满足 ${(a - \sqrt{8})}^{2}$ + $\sqrt{b - 4}$ +|c﹣2 $\sqrt{6}$ |=0，判断△ABC是否构成直角三角形，并说明理由．

查看试题解析

四、综合题

20. 【阅读材料】小明在学习二次根式时，发现一些含根号的式子可以化成另一个式子的平方，
如： $5 + 2 \sqrt{6} = (2 + 3) + 2 \sqrt{2 \times 3} = {(\sqrt{2})}^{2} + {(\sqrt{3})}^{2} + 2 \sqrt{2} \times \sqrt{3} = (\sqrt{2} + \sqrt{3})$ $8 + 2 \sqrt{7} = (1 + 7) + 2 \sqrt{1 \times 7} = 1^{2} + {(\sqrt{7})}^{2} + 2 \times 1 \times \sqrt{7} = {(1 + \sqrt{7})}^{2}$

(1)、【类比归纳】
请你仿照小明的方法将 $7 + 2 \sqrt{10}$ 化成另一个式子的平方．

(2)、【变式探究】
若 $a + 2 \sqrt{21} = {(\sqrt{m} + \sqrt{n})}^{2}$ 且a，m，n均为正整数，求a值.

查看试题解析
21. 材料：如何将双重二次根式 $\sqrt{a \pm 2 \sqrt{b}} (a > 0$ ， $b > 0$ ， $a \pm 2 \sqrt{b} > 0)$ 化简呢？如能找到两个数 $m$ ， $n (m > 0 ， n > 0)$ ，使得 $(\sqrt{m})^{2} + (\sqrt{n})^{2} = a$ ，即 $m + n = a$ ，且使 $\sqrt{m} \cdot \sqrt{n} = \sqrt{b}$ ，即 $m \cdot n = b$ ，那么 $a \pm 2 \sqrt{b} = (\sqrt{m})^{2} + (\sqrt{n})^{2} \pm 2 \sqrt{m} \cdot \sqrt{n} = (\sqrt{m} \pm \sqrt{n})^{2}$ $∴$ $\sqrt{a \pm 2 \sqrt{b}} = | \sqrt{m} \pm \sqrt{n} |$ ，双重二次根式得以化简.
例如化简： $\sqrt{3 \pm 2 \sqrt{2}}$ ，
因为 $3 = 1 + 2$ 且 $2 = 1 \times 2$ ，
$∴ 3 \pm 2 \sqrt{2} = (\sqrt{1})^{2} + (\sqrt{2})^{2} \pm 2 \sqrt{1} \times \sqrt{2} ∴ \sqrt{3 \pm 2 \sqrt{2}} = | 1 \pm \sqrt{2} |$ ，
由此对于任意一个二次根式只要可以将其化成 $\sqrt{a \pm 2 \sqrt{b}}$ 的形式，且能找到 $m$ ， $n (m > 0 ， n > 0)$ 使得 $m + n = a$ ，且 $m \cdot n = b$ ，那么这个双重二次根式一定可以化简为一个二次根式.
请同学们通过阅读上述材料，完成下列问题：

(1)、填空： $\sqrt{5 \pm 2 \sqrt{6}}$ = ， $\sqrt{12 \pm 2 \sqrt{35}}$ =；

(2)、化简： $\sqrt{9 \pm 6 \sqrt{2}}$ ；

(3)、计算： $\sqrt{3 - \sqrt{5}}$ + $\sqrt{2 \pm \sqrt{3}}$ .

查看试题解析
22. 如图，在下面的直角坐标系中，已知A（0，a），B（b，0），C（b，4）三点，其中a，b满足关系式 $a = \frac{\sqrt{b^{2} - 9} + \sqrt{9 - b^{2}}}{b + 3} + 2$ .

(1)、求a，b的值；

(2)、如果在第二象限内有一点P(m， $\frac{1}{3}$ )，请用含m的式子表示四边形ABOP的面积；

(3)、在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等?若存在，求出点P的坐标；若不存在，请说明理由.

查看试题解析
23. 先观察下列的计算，再完成练习．
（1） $\frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$ ；
（2） $\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ；
（3） $\frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$ ．
请你分析、归纳上面的解题方式，解决如下问题：

(1)、化简： $\frac{1}{\sqrt{5} + \sqrt{4}}$ ；

(2)、已知n是正整数，求 $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ 的值：

(3)、计算： $(\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + ⋯ + \frac{1}{\sqrt{2023} + \sqrt{2022}}) \times (\sqrt{2023} + 1)$ ．

查看试题解析

（北师大版）2023-2024学年八年级数学上册2.7 二次根式 同步测试

一、选择题

二、填空题

三、解答题

四、综合题

（北师大版）2023-2024学年八年级数学上册2.7 二次根式同步测试